
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие об аэро- и космических съёмках, схема получения первичной информации. Задачи, решаемые по материалам акс, достоинство недостатки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Схема получения первичной информации. Информационные канал «местность-снимок». Рассмотрим общую схему получения первичной видеоинформации при проведении аэро- и космических съемок земной поверхности. При съемке в отраженных лучах радиационный поток проходит путь от источника излучения до объекта через атмосферу, где происходят его энергетические изменения. Характеристики информационного канала «Местность – снимок». Потери информации об объектах аэроландшафта в данном канале. Математические и эмпирические зависимости. Фотометрические величины. Фотометри́ческая величина́ — аддитивная физическая величина, определяющая временно́е, пространственное, спектральное распределение энергии оптического излучения и свойств веществ, сред и тел как посредников переноса или приемников энергии (определение взято из ГОСТ 26148—84[1]). Фотометрические величины используются в фотометрии, оптикеи других отраслях науки и техники. По количественному выражению фотометрические величины делятся на следующие группы:
По широте использования среди редуцированных фотометрических величин выделяются световые величины. Распределения фотометрических величин во времени, пространстве и по спектру описываются с помощью:
Средством измерения фотометрических величин служат фотометры. Устройствыо кадрового АФА. В корпусе кадрового АФА расположены объектив, затвор и распределительный механизм. Верхнее основание корпуса является прикладной рамкой,к которой при помощи выравнивающего устройства (прижимного столика и выравнивающего стекла) прижимается в момент экспонирования фотоплёнка. На прикладной рамке нанесены координатные метки, определяющие положение координатных осей аэрофотоснимка. В верхней части корпуса смонтирована кассета II, в нижней - установлены светофильтры и защитная бленда. В кассете размещена плёнка, которая в процессе аэрофотосъёмки перематывается с катушки на катушку '. Корпус аэрокамеры прикреплён к аэрофотоустановке III, которая предназначена для монтирования АФА над люком самолёта, сохранения нужного его положения и уменьшения вибраций, возникающих от работы мотора и толчков при взлёте и посадке. Простейшая аэрофотоустановка III состоит из металлического каркаса в виде кольца и укреплённого внутри него карданного устройства. Каркас опирается на корпус самолёта при помощи пружинных амортизаторов. Кадровые АФА, которые предназначены для съемки с больших высот. Имеют оптическую или механическую компенсацию сдвига изображения. К ним относятся АФА - МК, НАФА - МК /ночной/, АФА -42, АФА - 40. Кадровые АФА без компенсации сдвига изображения относятся к группе специальных АФА. Отличаются небольшими размерами кадров /менее 18 х 18 см/ и небольшими фокусными расстояниям аэрофотообъективов. К ним относятся АФА - 39, АФА - БА. Физическое созревание Первое созревание — физическое — заключается в выдерживании фотографической эмульсии при постоянной температуре и помешивании. За время созревания происходит непрерывное уменьшение числа микрокристаллов и увеличение их среднего размера, вызываемое растворением более мелких кристаллов и роста за их счёт более крупных. Фотографическая желатина во время эмульсификации и первого созревания препятствует слипанию микрокристаллов галогенидов серебра и их выпадению на дно сосуда. После завершения первого созревания фотографическая эмульсия студенится понижением температуры, затем измельчается в продолговатые кусочки — «червяки», которые несколько часов промывают проточной водой. Промывка нужна для удаления побочных веществ: аммиака, азотнокислого калия, избытка бромистого калия и других веществ, образовавшихся при эмульсификации. У некоторых видов эмульсий для фотобумаг промывка исключается из производственного цикла. Химическое созревание После завершения промывки следует стадия второго, или химического, созревания. Во время его на поверхности эмульсионных микрокристаллов, сформированных в первом созревании, происходят химические процессы. Они заключаются во взаимодействии бромистого серебра с примесями, содержащимися в желатине, в результате чего образуются центры созревания, которые состоят из ничтожно малых количеств металлического и сернистого серебра. Под влиянием температуры центры созревания постепенно перерастают в центры светочувствительности, наличие которых обусловливает светочувствительность. После завершения второго созревания эмульсия вновь студенится и хранится при температуре 4-6 °C до нанесения на подложку. Полив Процесс подготовки эмульсии к поливу заключается в ее расплавлении до жидкого состояния, фильтрации и введения следующих веществ:
Когда физико-химические свойства эмульсии достигнут заданных параметров, её с помощью поливочных машин наносят на соответствующую подложку и подвергают сушке при строго определённой температуре и влажности. Особое значение при сушке имеет воздух, который тщательно очищается от пыли. Нарушение режима сушки и её продолжительности даёт брак. Состав и расходы фотоэмульсии [править | править исходный текст] Готовая эмульсия содержит обычно по весу около 6 % сухой желатины и 4 % галоидного серебра. На каждый квадратный метр готовых негативных материалов расходуется от 12 до 15 г, а позитивных — от 1,5 до 8 г серебра. Стр 46 учебника Деформации В идеальной центр. проекц. точка изобр., центр проекции и точка местности наход. на одной прямой- УСЛОВИЕ КОЛЛИНЕАРНОСТИ. Основные факторы, вызывающие нарушение условий коллинеарности проектирующих лучей, проявляют свое действие совместно. Исключить или уменьшить их влияние можно путем выбора соотв съемочных средств и условий проведения съемок или учитывая их при фотограм обработке. а)Рефракция света в атмосфере. Атмосфера – некая среда, состоящая из газов, водяных паров, механических включений. 1) условие коллиниарности – условие для фотограмметрии(рис: от поверх земли до снимка проходит луч, проходящий через S). 2) условие изоморфизма – условие для дешифр. В(объект) стрелка в обе стороны D(цвет). ИИ(источник излучения) – объект. Атмосфера на излучение воздействует двояко: 1) изменяет спектральный состав проходящего излучения. 2) геометрическое искажение излучение, нарушение прямолинейности в лучах. б) рефракция в защитном стекле фотолюка. В результате разности температур и давления воздуха на внешней поверхности стекла люка защитное стекло прогибается, возникает кривизна и клиновидность. Происходит отклонение луча,что вызывает дефокусировку камеры и искажает ортоскопию изображения. в) рефракция в светофильтре вызвана не параллельностью его сторон, в зависимости от качества изготовления может достигать несколько мкм. г) дисторсия объектива аэрофотоаппарата. В топо графич АФА дисторсия равна 2-3мкм, в нефото –сотые доли мм. д)фото смаз изображения. Вызван линейными и угловыми перемещениями оптического изображения относительно фотопленки при фотографировании,в зависимости от метода фотограмметрической обработке снимов допускается в пределах 0,02-0,05мм. е) отклонение поверхности аэрофотопленки от фокальной плоскости АФА. Определяется размером зазора между светочувствительными слоем и плоскостью прикладной рамки и составляет 5-30 мкм. ж) остаточная погрешность выравнивания пленки в плоскость. Для уменьшения геометр искажений и повышения резкости изображения в АФА пленка перед экспонированием выравнивается в плоскость. Погрешность выравниваея зависит: от способа выравнивания пленки, клиновидности, отлщины и размера прогиба выравнивающего стекла. В центральной части невыранивание пленки вызывает смещение изображение на 2-2,5 мкм, а на краю м.б. 150 мкм. з0) неравномерность толщины фотоэмульсионного слоя в аэропленке. При ее изготовлении фотоэмульсионный слой наносят на основу. Толщина слоя в пределах снимка неодинакова. Для пленок на триацетатной основе изменение толщины эмульсионного слоя не превышает 2мкм на 10 мм. Смещение точки изображения в центральной части снимка примерно равна 2 мкм, на краю м.б. 20 мкм. Деформация пленки после сушки после фотохим обработки и хранения снимков. Продольное и поперечное перекрытие снимков. Требования к величинам перекрытий. перекрытие фотоснимков в процессе аэрофотосъемки по маршруту (а) (продольное перекрытие) и между двумя смежными маршрутами (б) (поперечное перекрытие) с целью исключения разрывов в изображаемой на них местности и возможности получения стереоскопического эффекта. Допустимое минимальное продольное перекрытие - 56 %, оптимальное - 60, в горной местности - 70 %. Правильность продольного перекрытия проверяется соответствием фактического и расчетного количества снимков в маршруте. Схема продольного (а) и поперечного (б) перекрытий в маршрутах полетов при аэрофотосъемке площади лесов. Допустимое минимальное поперечное перекрытие -- 20 %, оптимальное -- 30 %. Проверка поперечных перекрытий аэрофотоснимков выполняется по измерениям аэрофотоснимков соседних маршрутов при совмещении перекрывающейся части маршрута. При двухкамерной аэрофотосъемке минимальное поперечное перекрытие на первом аэрофотоаппарате должно быть 30, а на втором -- 15 %. Перекрытие аэрофотоснимков в направлении маршрута съемки называется продольным и обозначается буквой p. Перекрытие аэрофотоснимков смежных маршрутов называется поперечным и обозначается буквой q. Величины перекрытий выражаются в процентах относительно размера соответствующей стороны аэрофотоснимка. Продольное и поперечное перекрытия необходимы для связи аэрофотоснимков в общую систему при их фотограмметрической обработке. И 36 По лекции 38-39 Для установления связей между точками объекта и их фотографическими изображениями используются пространственные и плоские системы координат. Если картографируемый участок захватывает больше, чем 1 зону может использоваться геоцентрическая система координат (рис.5).
В ней за начало координат принят центр общеземного эллипсоида О' г, а плоскостью X' г Y' гявляется плоскость экватора. Ось X' г находится в плоскости начального меридиана, а ось Z' г совмещена с полярной осью О' г Р. Система координат правая. За фигуру Земли принимается эллипсоид вращения с полуосями а и b и сжатием е. Любая точка О пространства задаётся геодезическими координатами: широтой В, долготой L и высотой Н. Геоцентрические координаты X' г, Y' г, Z' г точки О находят по их геодезическим координатам, с помощью известных формул сфероидической геодезии. Может использоваться и прямоугольная система координат X"г Y"г Z"г, представленная на рис.5. Она сохраняет все преимущества геоцентрической системы, но абсолютные значения координат точек в ней меньше. Ось Z"г нормальна к поверхности эллипсоида в начальной точке О картографируемого участка; ось Y"г совпадает с направлением на север. Система координат правая. За начало счёта высот принимается такое значение, при котором аппликаты всех точек положительны. Координаты X"г, Y"г, Z"г, легко получаются из геоцентрических X'г, Y'г, Z'г путём трёхмерного преобразования, включающего перенос начала координат и их вращение. При решении задач на сравнительно небольшом участке местности используется известная левая система прямоугольных координат O На практике часто находит применение местная система пространственных прямоугольных координат Xг Yг Zг с началом в некоторой точке А картографируемого участка (рис.6). В этой системе ось Zг нормальна к поверхности квазигеоида в точке А, ось Xг горизонтальна и параллельна осевому меридиану зоны, в которой находится участок съёмки, а ось Yг направлена на восток. Координаты начала задаются в системе Ог Xг Yг Zг. На каждом снимке по его периметру имеется ряд координатных меток, которые определяют плоскую прямоугольную систему координат o' x y. Такая система при наличии на снимке четырёх меток 1, 2, 3, 4 показана на рис. 7. Начало координат находится в точке о' пересечение отрезков 1-2 и 3-4. Ось x совмещается с прямой 1-2, а ось y с перпендикуляром к оси x в точке о'. Возможны и другие варианты. Например, ось y – это главная вертикаль, а ось x - одна из горизонталей и т. д. Отметим, что на наземных снимках оси обозначают буквами x и z, а координаты в системе координат снимка иногда называют фотокоординатами. Положение точка на снимке определяется координатами x и y, но это можно сделать и в пространственной фотограмметрической системе X'Y'Z' (рис.8). Начало координат этой системы всегда совмещено с точкой фотографирования S, а оси X', Y', Z' параллельны осям X, Y, Z фотограмметрической системы координат точек объекта местности или осям геодезической системы координат. Связи между плоскими и пространственными координатами точек снимка и местности устанавливаются через элементы ориентирования снимка. 39)
Элементы внешнего ориентирования (ЭВО) позволяют установить положение снимка (связки), которое она занимала в момент фотографирования относительно заданной пространственной прямоугольной системы координат. Для снимков, полученных АФА, на практике используют две таких системы. В первую систему ЭВО (рис. 10) входят координаты Xs, Ys, Zs точки фотографирования, а также углы поворота снимка α, ω и κ Продольный угол наклона снимка α образуется осью Z΄ и проекцией главного луча Sо на плоскость X΄ Z΄. Поперечный угол наклона снимка ω заключён между главным лучом Sо и его проекцией на плоскость X΄ Z΄. Угол поворота снимка κ образуют ось у снимка и след плоскости, проходящей через главный луч Sо и ось Y΄ (в этой плоскости находится угол ω). На рис. 10 углы κ и ω положительные, угол α - отрицательный. Вторая система (рис.11) ЭВО содержит: координаты Xs, Ys, Zs точки фотографирования; t – дирекционный угол оптической оси фотокамеры – он образуется следом плоскости главного вертикала W и положительным направлением оси X΄; ε - угол наклона снимка, находится в плоскости главного вертикала между главным и надирным лучами; κ – угол поворота в плоскости снимка, образуется главной вертикалью
40) уравнение коллинеарности:
41) Зависимость между координатами горизонтального и наклонного снимков можно отметить с помощью строгих и простых соотношений. Их можно написать, если начало координат на снимке и на местности совместить с точкой нулевых искажений с:
Из зависимостей между координатами горизонтального и наклонного снимков можно сделать вывод:
Это означает, что если наклонный снимок совместить с горизонтальным, вращением его вокруг линии неискаженных масштабов (рис. 13.) то соответствующие точки окажутся на одном луче, проходящем через точку нулевых искажений c.
Величину максимального смещения точек можно оценивать по приближенной формуле:
Рельеф местности также вызывает смещение точек, причем по направлениям проходящим через точку надира n, в которую сходятся изображения отвесных прямых. То есть, если h - превышение точки А над точкой В, расположенной в плоскости предмета, и отрезок АВ отвесный, то точка а на снимке сместится относительно точки b на величину ab = δrh (рис. 14). При h > 0 смещение происходит от точки надира, когда h < 0, – к точке надира.
Стереоскопический эффект Представим, что используемые ранее точки пространства А и D регистрируются двумя камерами с фокусным расстоянием f, расположенными на концах базиса съемки В=br (рис. 1).
В плоскости негативов Если реальные точки А и D заменить парой позитивных изображений Два смежных частично перекрывающихся снимка, полученных с концов некоторого базиса, называют стереопарой, или парой снимков. Теперь, очевидно, стало более понятным требование обеспечения определенного продольного перекрытия снимков (примерно 60 % при съемке равнины). Сокращение перекрытия может привести к риску образования разрывов между стереомоделями и соответственно к усложнению или невозможности процесса получения трехмерной метрической информации со снимков. Увеличение перекрытий уменьшит углы засечки наблюдаемых точек, что приведет к снижению точности в определении разностей их отстояний (превышений). Если снимки перед глазами поменять местами, то наблюдатель также увидит стереомодель, но с обратным стереоэффектом — удаленные элементы ландшафта будут восприниматься близкими, и наоборот, близкие элементы покажутся удаленными. Этот вариант стереоскопического наблюдения снимков используют при анализе отрицательных микроформ рельефа (промоин, канав, кюветов и др.). Может быть еще вариант наблюдения пары снимков, при котором оба снимка развертываются в своей плоскости на 90°. Наблюдатель при этом вне зависимости от рельефа увидит плоское пластичное изображение местности. Стереоэффект, получаемый при этом, называют нулевым. Точность (детальность) стереоскопического восприятия по снимкам элементов пространственных объектов зависит, как уже отмечалось, от угла засечки этих элементов. Значение угла определяется размерами базиса В и высотой съемки Н. Точность восприятия стереомодели зависит также от условий наблюдения снимков. Минимальная разность отстояний (высот) наблюдаемых точек для расстояния наилучшего видения (250 мм)
где v — увеличение стереоприбора; b — базис съемки в масштабе снимков. Пользуясь этой формулой, вычислим При высотах съемки 500,1000, 2000 и 5000 м значения По снимкам, полученным с космических платформ с высоты 300 и 900 км, значения Точность восприятия превышений при наблюдении космических снимков можно повышать, увеличивая базис съемки. Сделать это можно за счет увеличения угла поля изображения съемочной системы или использования конвергентной съемки. В первом случае могут быть варианты: увеличение формата кадра или уменьшение фокусного расстояния съемочной камеры. Последний вариант приведет к уменьшению съемочного масштаба и геометрического разрешения снимков. 43) Главной задачей фотограмметрии в применении ее для топографии является определение координат точек местности по аэрофотоснимкам. Используя одиночный аэрофотоснимок, можно определить лишь плановое положение точек, изобразившихся на нем. Для определения высот точек местности необходимо иметь два аэрофотоснимка данного участка, полученных из двух разных точек или с двух концов базиса фотографирования. Два снимка с изображениями одного и того же участка местности, полученные с двух точек пространства, называются стереоскопической парой снимков (стереопарой). Снимок, полученный с точки фотографирования S 1, называется левым, а с S 2 – правым. На рис. 19 изображена пара снимков в положении, которое она занимала в момент фотографирования. ^ А – точка местности, изобразившаяся на снимках в точках а 1 и а 2.
Расстояние ^ В между точками фотографирования S 1 и S 2 – базис фотографирования. Плоскость W A, проходящая через базис и точку А местности есть базисная плоскость. Плоскости, проходящие через базис фотографирования и главные лучи являются главными базисными плоскостями (W 1 - левого W 2 - правого снимков). Любая пара соответственных лучей пересекается, если снимки занимают положение, которое было в момент фотографирования. Совокупность их точек пересечения образует поверхность. Ее называют стереомоделью или просто моделью местности. При выше названных условиях она совпадает с земной поверхностью, значит масштаб такой модели 1:1. Представим теперь, что одна из связок (например, правая) поступательно перемещается вдоль базиса из положения S2 в S2¢. Модель при этом не разрушится, но изменится ее масштаб. Расстояние b п между центрами проекций двух связок, по которым построена модель, называется базисом проектирования. Ее масштаб вычисляется по формуле:
Взаимное ориентирование снимков стереопары это установка их в положение, при котором любая пара соответственных лучей пересекается, то есть обеспечивается построение модели. Величины, определяющие такое положение снимков, называются элементами взаимного ориентирования (ЭвзО). На практике выполнение условия пересечения соответственных лучей достигается поворотом обоих снимков или поворотами и смещениями только одного из них при неподвижном положении второго. В соответствии с этим различают две системы элементов взаимного ориентирования. В первой неподвижными считают базис фотографирования и главную базисную плоскость левого снимка; во второй – левый снимок. Первая система элементов. Начало системы координат S1X1'Y1'Z1'– в центре проекции S1 левого снимка Р1 (рис. 21). Ось X1' совмещена с базисом фотографирования, а ось Z1' установлена в главной базисной плоскости левого снимка. Система координат S2X2'Y2'Z2' параллельна системе координат S1X1'Y1'Z1'. Элементами взаимного ориентирования являются:
Элементами взаимного ориентирования являются:
Рис. 3. Изображение отвесной линии на паре снимков идеального случая съемки Разность ординат соответственных точек пары снимков называют поперечным параллаксом точки:
На реальных снимках в общем случае q
Из этого можно сделать вывод: поперечные параллаксы являются функцией некоторых величин, определяющих взаимное положение пары снимков (элементов взаимного ориентирования снимков). Разность абсцисс пары соответственных точек на левом и правом снимках называют продольным параллаксом точки:
На реальных снимках абсциссы и соответственно продольные параллаксы будут искаженными (вспомним о смещении точек снимка вследствие его наклона). Следовательно, продольные параллаксы определяемых точек предварительно должны быть освобождены от искажений, т. е. трансформированы. Аналогично предыдущему трансформированные абсциссы и продольные параллаксы обозначают добавочным символом:
50) на стереопаре снимков (прямая фотограмметрическая засечка).
Рис.1.7.1 p=x1-x2 – продольный параллакс; q=y1-y2 – поперечный параллакс.

Рис.1.7.2
На рис.1.7.2 показана стереопара снимков Р1 и Р2, на которых точка местности М изобразилась соответственно в точках m1 и m2. Будем считать, что элементы внутреннего и внешнего ориентирования снимков известны. Выведем формулы связи координат точек местности и координат их изображений на стереопаре снимков. Из рис.1.7.2 следует, что векторы Векторы Из рис.1.7.2 следует, что
Так как векторы
где N – скаляр. С учетом (1.7.2) выражение (1.8.1) будет иметь вид
В координатной форме выражение (1.7.3) будет иметь вид
где X1’,Y1’,Z1’ –координаты вектора
Найдем значение N, входящее в выражение (1.7.4). Из рис.1.7.2 следует, что
или с учетом (1.7.2)
Так как векторы
С учетом (1.7.5) выражение (1.7.6) можно представить в виде
или
Выражение (1.7.7) можно представить в виде
или
где
BX, BY, BZ, X1’, Y1’, Z1’, X1’, Y1’, Z1’ – координаты векторов
где i – номер снимка, а
Так как векторы
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.210.196 (0.014 с.) |

 и осью y плоской системы координат x y.
и осью y плоской системы координат x y.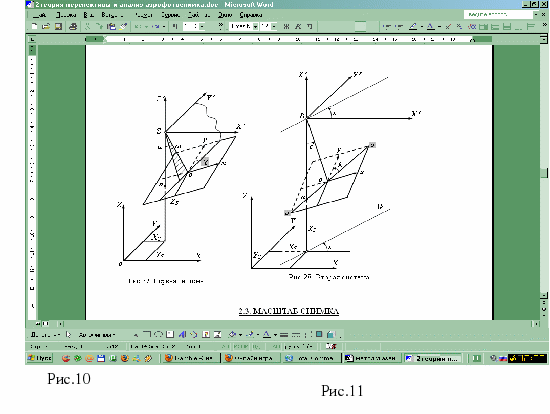

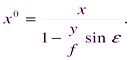 ,
, 

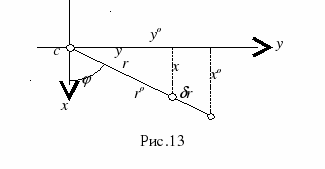
 .
.
 возможно как в сторону точки нулевых искажений, при jÎ(0°, 180°), так и в противоположную сторону. Максимально оно на главной вертикали (φ равно 90° или 270°). На линии неискаженных масштабов точки за наклон не смещаются.
возможно как в сторону точки нулевых искажений, при jÎ(0°, 180°), так и в противоположную сторону. Максимально оно на главной вертикали (φ равно 90° или 270°). На линии неискаженных масштабов точки за наклон не смещаются.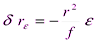 .
.

 .
.
 можно в ряде случаев с достаточной для практики точностью определить высоту отдельных объектов (дерева, столба, здания, трубы и т. д.).
можно в ряде случаев с достаточной для практики точностью определить высоту отдельных объектов (дерева, столба, здания, трубы и т. д.).
 и
и  точки А и D изобразятся соответственно точками а1 и а2, d1 и d2. Направление проектирующих лучей, а следовательно, и значения углов
точки А и D изобразятся соответственно точками а1 и а2, d1 и d2. Направление проектирующих лучей, а следовательно, и значения углов  и
и  останутся теми же, что и при наблюдении этих точек человеком.
останутся теми же, что и при наблюдении этих точек человеком. и
и  так, чтобы левый глаз наблюдателя видел только левый снимок, а правый глаз — только правый снимок, на сетчатке глаз возникнет ситуация, существовавшая при непосредственном наблюдении этих точек. Наблюдатель воспримет пару плоских изображений пространственно. Такое восприятие называют прямым стереоэффектом, а мнимое пространственное изображение снятого объекта, воспринимаемое наблюдателем, — стереоскопической моделью (стереомоделью). Стереомодель будет наблюдаться только в пределах перекрытия снимков.
так, чтобы левый глаз наблюдателя видел только левый снимок, а правый глаз — только правый снимок, на сетчатке глаз возникнет ситуация, существовавшая при непосредственном наблюдении этих точек. Наблюдатель воспримет пару плоских изображений пространственно. Такое восприятие называют прямым стереоэффектом, а мнимое пространственное изображение снятого объекта, воспринимаемое наблюдателем, — стереоскопической моделью (стереомоделью). Стереомодель будет наблюдаться только в пределах перекрытия снимков.
 для наблюдения снимков, полученных с некоторых высот, наиболее используемых при выполнении землеустроительных и кадастровых работ, а также при дистанционном зондировании. При этом примем, что наблюдаются снимки формата 18 х 18 см с продольным перекрытием 60 % с использованием стереоскопа с полуторакратным увеличением.
для наблюдения снимков, полученных с некоторых высот, наиболее используемых при выполнении землеустроительных и кадастровых работ, а также при дистанционном зондировании. При этом примем, что наблюдаются снимки формата 18 х 18 см с продольным перекрытием 60 % с использованием стереоскопа с полуторакратным увеличением.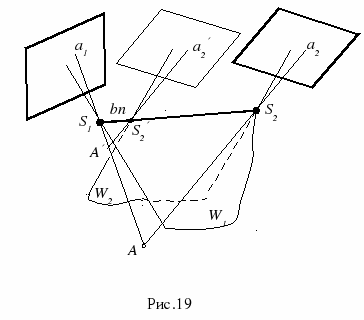

 - угол в главной базисной плоскости левого снимка между осью Z 1 ' и главным лучом связки;
- угол в главной базисной плоскости левого снимка между осью Z 1 ' и главным лучом связки; - угол на левом снимке между осью y 1 и следом плоскости
- угол на левом снимке между осью y 1 и следом плоскости  ;
; - угол в главной базисной плоскости левого снимка между осью Z 2 ' и проекцией главного луча правой связки на главную базисную плоскость левого снимка;
- угол в главной базисной плоскости левого снимка между осью Z 2 ' и проекцией главного луча правой связки на главную базисную плоскость левого снимка; - угол между проекцией главного луча правой связки на главную базисную плоскость левого снимка и главным лучом;
- угол между проекцией главного луча правой связки на главную базисную плоскость левого снимка и главным лучом; - угол на правом снимке между осью y 2 и следом плоскости
- угол на правом снимке между осью y 2 и следом плоскости  .
.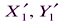 этой системы направлены параллельно соответствующим координатным осям x1, y1 левого снимка (рис. 22), а ось
этой системы направлены параллельно соответствующим координатным осям x1, y1 левого снимка (рис. 22), а ось  совпадает с главным лучом левой связки. Система координат
совпадает с главным лучом левой связки. Система координат 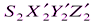 параллельна системе координат
параллельна системе координат  .
. - угол между осью
- угол между осью  и проекцией базиса на плоскость
и проекцией базиса на плоскость  (или элемент ориентирования By);
(или элемент ориентирования By);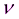 - угол наклона базиса S1S2 относительно плоскости
- угол наклона базиса S1S2 относительно плоскости  (или BZ);
(или BZ); - взаимный продольный угол наклона снимков, составленный осью
- взаимный продольный угол наклона снимков, составленный осью  с проекцией главного луча правой связки на плоскость
с проекцией главного луча правой связки на плоскость  ;
; - взаимный поперечный угол наклона снимков, заключённый между плоскостью
- взаимный поперечный угол наклона снимков, заключённый между плоскостью  и главным лучом правой связки;
и главным лучом правой связки; - взаимный угол поворота снимков, угол на правом снимке между осью y2 и следом
- взаимный угол поворота снимков, угол на правом снимке между осью y2 и следом  плоскости
плоскости 
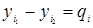
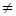 0. Такие снимки, если значение q превышает определенные допуски, преобразуют (трансформируют). Ординаты после преобразования называют трансформированными и обозначаются
0. Такие снимки, если значение q превышает определенные допуски, преобразуют (трансформируют). Ординаты после преобразования называют трансформированными и обозначаются 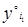 и
и 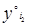 . Для трансформированных ординат должно выполняться условие:
. Для трансформированных ординат должно выполняться условие: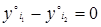
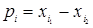
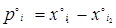


 определяют соответственно положение точки местности М и центра проекции S1 снимка Р1 относительно начала системы координат объекта OXYZ. Вектор
определяют соответственно положение точки местности М и центра проекции S1 снимка Р1 относительно начала системы координат объекта OXYZ. Вектор  определяет положение центра проекции S2 снимка Р2 относительно центра проекции S1.
определяет положение центра проекции S2 снимка Р2 относительно центра проекции S1.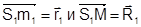 определяют положение точек m1 и М относительно центра проекции S1. Векторы
определяют положение точек m1 и М относительно центра проекции S1. Векторы 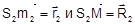 определяют положение точек m2 и М относительно центра проекции S2.
определяют положение точек m2 и М относительно центра проекции S2. (1.7.1)
(1.7.1) коллинеарные, то
коллинеарные, то ; (1.7.2)
; (1.7.2) . (1.7.3)
. (1.7.3)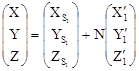 ; (1.7.4)
; (1.7.4) в системе координат объекта OXYZ.
в системе координат объекта OXYZ. .
. ;
; . (1.7.5)
. (1.7.5) . (1.7.6)
. (1.7.6) ;
; . (1.7.7)
. (1.7.7) ;
; ; (1.7.8),
; (1.7.8), - орты, совпадающие с осями координат X,Y,Z системы координат объекта OXYZ;
- орты, совпадающие с осями координат X,Y,Z системы координат объекта OXYZ; в системе координат объекта OXYZ.
в системе координат объекта OXYZ. ;
;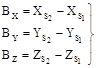 . (1.7.9)
. (1.7.9) коллинеарные (потому что векторы
коллинеарные (потому что векторы  комплан
комплан 


