
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы ориентирования одиночного снимкаСодержание книги
Поиск на нашем сайте
Различают элементы внутреннего и внешнего ориентирования снимка. Элементы внутреннего ориентирования определяют положение центра проекции S относительно снимка. Ими являются координаты точки S в пространственной системе координат снимка (рис. а). Поскольку проекцией точки S на плоскости снимка является главная точка о, то их плановые координаты хи^в системе координат снимка совпадают, аппликатой точки S является расстояние So, т. е. фокусное расстояние АФА/ Таким образом, элементами внутреннего ориентирования снимка являются координаты главной точки снимка хь, уо и фокусное расстояние АФА / Эти элементы почти всегда известны с высокой точностью и записаны в паспорте АФА. Например,/= 100,020 мм; xq = -0,012 мм; у0 = +0,023 мм. Элементы внутреннего ориентирования снимка формируют связку проектирующих лучей, существовавшую при съемке. Ее положение в пространстве определяют элементы внешнего ориентирования снимка. Их шесть. Это три линейных элемента — гео- координаты центра проекции S (Xs, Ys, Zs) и три угловых элемента наклона и поворота снимка: альфе — продольный угол наклона снимка (угол между осью Z и проекцией главного луча на плоскость XZ); тета — поперечный угол наклона снимка (угол между главным лучом и проекцией главного луча на плоскость XZ); капа — угол поворота снимка (угол на снимке между осью у и следом сечения плоскости снимка с плоскостью, построенной на главном луче и оси Y). В аналитической фотограмметрии горизонтальным снимком называют снимок, все три угла наклона и поворота которого равны нулю, т. е. а = со = ае = 0. Следует заметить, что для всех снимков, полученных данным АФА, элементы внутреннего ориентирования можно считать постоянными известными величинами. Однако элементы внешнего ориентирования у каждого снимка свои и, как правило, неизвестны. Задачу по определению геодезических координат точки местности по измеренным координатам ее изображения на снимке называют прямой фотограмметрической засечкой.(рисунок в лекции, он такой же как и выше) По лекции 38-39 Для установления связей между точками объекта и их фотографическими изображениями используются пространственные и плоские системы координат. Если картографируемый участок захватывает больше, чем 1 зону может использоваться геоцентрическая система координат (рис.5).
В ней за начало координат принят центр общеземного эллипсоида О' г, а плоскостью X' г Y' гявляется плоскость экватора. Ось X' г находится в плоскости начального меридиана, а ось Z' г совмещена с полярной осью О' г Р. Система координат правая. За фигуру Земли принимается эллипсоид вращения с полуосями а и b и сжатием е. Любая точка О пространства задаётся геодезическими координатами: широтой В, долготой L и высотой Н. Геоцентрические координаты X' г, Y' г, Z' г точки О находят по их геодезическим координатам, с помощью известных формул сфероидической геодезии. Может использоваться и прямоугольная система координат X"г Y"г Z"г, представленная на рис.5. Она сохраняет все преимущества геоцентрической системы, но абсолютные значения координат точек в ней меньше. Ось Z"г нормальна к поверхности эллипсоида в начальной точке О картографируемого участка; ось Y"г совпадает с направлением на север. Система координат правая. За начало счёта высот принимается такое значение, при котором аппликаты всех точек положительны. Координаты X"г, Y"г, Z"г, легко получаются из геоцентрических X'г, Y'г, Z'г путём трёхмерного преобразования, включающего перенос начала координат и их вращение. При решении задач на сравнительно небольшом участке местности используется известная левая система прямоугольных координат O На практике часто находит применение местная система пространственных прямоугольных координат Xг Yг Zг с началом в некоторой точке А картографируемого участка (рис.6). В этой системе ось Zг нормальна к поверхности квазигеоида в точке А, ось Xг горизонтальна и параллельна осевому меридиану зоны, в которой находится участок съёмки, а ось Yг направлена на восток. Координаты начала задаются в системе Ог Xг Yг Zг. На каждом снимке по его периметру имеется ряд координатных меток, которые определяют плоскую прямоугольную систему координат o' x y. Такая система при наличии на снимке четырёх меток 1, 2, 3, 4 показана на рис. 7. Начало координат находится в точке о' пересечение отрезков 1-2 и 3-4. Ось x совмещается с прямой 1-2, а ось y с перпендикуляром к оси x в точке о'. Возможны и другие варианты. Например, ось y – это главная вертикаль, а ось x - одна из горизонталей и т. д. Отметим, что на наземных снимках оси обозначают буквами x и z, а координаты в системе координат снимка иногда называют фотокоординатами. Положение точка на снимке определяется координатами x и y, но это можно сделать и в пространственной фотограмметрической системе X'Y'Z' (рис.8). Начало координат этой системы всегда совмещено с точкой фотографирования S, а оси X', Y', Z' параллельны осям X, Y, Z фотограмметрической системы координат точек объекта местности или осям геодезической системы координат. Связи между плоскими и пространственными координатами точек снимка и местности устанавливаются через элементы ориентирования снимка. 39)
Элементы внешнего ориентирования (ЭВО) позволяют установить положение снимка (связки), которое она занимала в момент фотографирования относительно заданной пространственной прямоугольной системы координат. Для снимков, полученных АФА, на практике используют две таких системы. В первую систему ЭВО (рис. 10) входят координаты Xs, Ys, Zs точки фотографирования, а также углы поворота снимка α, ω и κ Продольный угол наклона снимка α образуется осью Z΄ и проекцией главного луча Sо на плоскость X΄ Z΄. Поперечный угол наклона снимка ω заключён между главным лучом Sо и его проекцией на плоскость X΄ Z΄. Угол поворота снимка κ образуют ось у снимка и след плоскости, проходящей через главный луч Sо и ось Y΄ (в этой плоскости находится угол ω). На рис. 10 углы κ и ω положительные, угол α - отрицательный. Вторая система (рис.11) ЭВО содержит: координаты Xs, Ys, Zs точки фотографирования; t – дирекционный угол оптической оси фотокамеры – он образуется следом плоскости главного вертикала W и положительным направлением оси X΄; ε - угол наклона снимка, находится в плоскости главного вертикала между главным и надирным лучами; κ – угол поворота в плоскости снимка, образуется главной вертикалью
40) уравнение коллинеарности:
41) Зависимость между координатами горизонтального и наклонного снимков можно отметить с помощью строгих и простых соотношений. Их можно написать, если начало координат на снимке и на местности совместить с точкой нулевых искажений с:
Из зависимостей между координатами горизонтального и наклонного снимков можно сделать вывод:
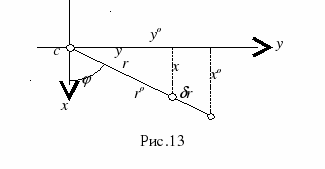
Это означает, что если наклонный снимок совместить с горизонтальным, вращением его вокруг линии неискаженных масштабов (рис. 13.) то соответствующие точки окажутся на одном луче, проходящем через точку нулевых искажений c.
Величину максимального смещения точек можно оценивать по приближенной формуле:
Рельеф местности также вызывает смещение точек, причем по направлениям проходящим через точку надира n, в которую сходятся изображения отвесных прямых. То есть, если h - превышение точки А над точкой В, расположенной в плоскости предмета, и отрезок АВ отвесный, то точка а на снимке сместится относительно точки b на величину ab = δrh (рис. 14). При h > 0 смещение происходит от точки надира, когда h < 0, – к точке надира.
Стереоскопический эффект Представим, что используемые ранее точки пространства А и D регистрируются двумя камерами с фокусным расстоянием f, расположенными на концах базиса съемки В=br (рис. 1).
В плоскости негативов Если реальные точки А и D заменить парой позитивных изображений Два смежных частично перекрывающихся снимка, полученных с концов некоторого базиса, называют стереопарой, или парой снимков. Теперь, очевидно, стало более понятным требование обеспечения определенного продольного перекрытия снимков (примерно 60 % при съемке равнины). Сокращение перекрытия может привести к риску образования разрывов между стереомоделями и соответственно к усложнению или невозможности процесса получения трехмерной метрической информации со снимков. Увеличение перекрытий уменьшит углы засечки наблюдаемых точек, что приведет к снижению точности в определении разностей их отстояний (превышений). Если снимки перед глазами поменять местами, то наблюдатель также увидит стереомодель, но с обратным стереоэффектом — удаленные элементы ландшафта будут восприниматься близкими, и наоборот, близкие элементы покажутся удаленными. Этот вариант стереоскопического наблюдения снимков используют при анализе отрицательных микроформ рельефа (промоин, канав, кюветов и др.). Может быть еще вариант наблюдения пары снимков, при котором оба снимка развертываются в своей плоскости на 90°. Наблюдатель при этом вне зависимости от рельефа увидит плоское пластичное изображение местности. Стереоэффект, получаемый при этом, называют нулевым. Точность (детальность) стереоскопического восприятия по снимкам элементов пространственных объектов зависит, как уже отмечалось, от угла засечки этих элементов. Значение угла определяется размерами базиса В и высотой съемки Н. Точность восприятия стереомодели зависит также от условий наблюдения снимков. Минимальная разность отстояний (высот) наблюдаемых точек для расстояния наилучшего видения (250 мм)
где v — увеличение стереоприбора; b — базис съемки в масштабе снимков. Пользуясь этой формулой, вычислим При высотах съемки 500,1000, 2000 и 5000 м значения По снимкам, полученным с космических платформ с высоты 300 и 900 км, значения Точность восприятия превышений при наблюдении космических снимков можно повышать, увеличивая базис съемки. Сделать это можно за счет увеличения угла поля изображения съемочной системы или использования конвергентной съемки. В первом случае могут быть варианты: увеличение формата кадра или уменьшение фокусного расстояния съемочной камеры. Последний вариант приведет к уменьшению съемочного масштаба и геометрического разрешения снимков. 43) Главной задачей фотограмметрии в применении ее для топографии является определение координат точек местности по аэрофотоснимкам. Используя одиночный аэрофотоснимок, можно определить лишь плановое положение точек, изобразившихся на нем. Для определения высот точек местности необходимо иметь два аэрофотоснимка данного участка, полученных из двух разных точек или с двух концов базиса фотографирования. Два снимка с изображениями одного и того же участка местности, полученные с двух точек пространства, называются стереоскопической парой снимков (стереопарой). Снимок, полученный с точки фотографирования S 1, называется левым, а с S 2 – правым. На рис. 19 изображена пара снимков в положении, которое она занимала в момент фотографирования. ^ А – точка местности, изобразившаяся на снимках в точках а 1 и а 2.
Расстояние ^ В между точками фотографирования S 1 и S 2 – базис фотографирования. Плоскость W A, проходящая через базис и точку А местности есть базисная плоскость. Плоскости, проходящие через базис фотографирования и главные лучи являются главными базисными плоскостями (W 1 - левого W 2 - правого снимков). Любая пара соответственных лучей пересекается, если снимки занимают положение, которое было в момент фотографирования. Совокупность их точек пересечения образует поверхность. Ее называют стереомоделью или просто моделью местности. При выше названных условиях она совпадает с земной поверхностью, значит масштаб такой модели 1:1. Представим теперь, что одна из связок (например, правая) поступательно перемещается вдоль базиса из положения S2 в S2¢. Модель при этом не разрушится, но изменится ее масштаб. Расстояние b п между центрами проекций двух связок, по которым построена модель, называется базисом проектирования. Ее масштаб вычисляется по формуле:
Взаимное ориентирование снимков стереопары это установка их в положение, при котором любая пара соответственных лучей пересекается, то есть обеспечивается построение модели. Величины, определяющие такое положение снимков, называются элементами взаимного ориентирования (ЭвзО). На практике выполнение условия пересечения соответственных лучей достигается поворотом обоих снимков или поворотами и смещениями только одного из них при неподвижном положении второго. В соответствии с этим различают две системы элементов взаимного ориентирования. В первой неподвижными считают базис фотографирования и главную базисную плоскость левого снимка; во второй – левый снимок. Первая система элементов. Начало системы координат S1X1'Y1'Z1'– в центре проекции S1 левого снимка Р1 (рис. 21). Ось X1' совмещена с базисом фотографирования, а ось Z1' установлена в главной базисной плоскости левого снимка. Система координат S2X2'Y2'Z2' параллельна системе координат S1X1'Y1'Z1'. Элементами взаимного ориентирования являются:
Элементами взаимного ориентирования являются:
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1310; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.170.65 (0.011 с.) |

 и осью y плоской системы координат x y.
и осью y плоской системы координат x y.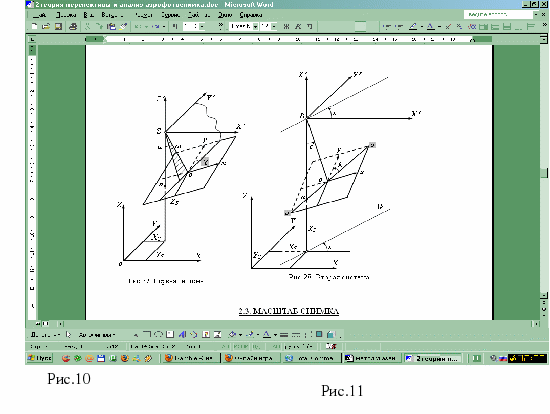

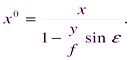 ,
, 

 .
.
 возможно как в сторону точки нулевых искажений, при jÎ(0°, 180°), так и в противоположную сторону. Максимально оно на главной вертикали (φ равно 90° или 270°). На линии неискаженных масштабов точки за наклон не смещаются.
возможно как в сторону точки нулевых искажений, при jÎ(0°, 180°), так и в противоположную сторону. Максимально оно на главной вертикали (φ равно 90° или 270°). На линии неискаженных масштабов точки за наклон не смещаются.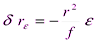 .
.

 .
.
 можно в ряде случаев с достаточной для практики точностью определить высоту отдельных объектов (дерева, столба, здания, трубы и т. д.).
можно в ряде случаев с достаточной для практики точностью определить высоту отдельных объектов (дерева, столба, здания, трубы и т. д.).
 и
и  точки А и D изобразятся соответственно точками а1 и а2, d1 и d2. Направление проектирующих лучей, а следовательно, и значения углов
точки А и D изобразятся соответственно точками а1 и а2, d1 и d2. Направление проектирующих лучей, а следовательно, и значения углов  и
и  останутся теми же, что и при наблюдении этих точек человеком.
останутся теми же, что и при наблюдении этих точек человеком. и
и  так, чтобы левый глаз наблюдателя видел только левый снимок, а правый глаз — только правый снимок, на сетчатке глаз возникнет ситуация, существовавшая при непосредственном наблюдении этих точек. Наблюдатель воспримет пару плоских изображений пространственно. Такое восприятие называют прямым стереоэффектом, а мнимое пространственное изображение снятого объекта, воспринимаемое наблюдателем, — стереоскопической моделью (стереомоделью). Стереомодель будет наблюдаться только в пределах перекрытия снимков.
так, чтобы левый глаз наблюдателя видел только левый снимок, а правый глаз — только правый снимок, на сетчатке глаз возникнет ситуация, существовавшая при непосредственном наблюдении этих точек. Наблюдатель воспримет пару плоских изображений пространственно. Такое восприятие называют прямым стереоэффектом, а мнимое пространственное изображение снятого объекта, воспринимаемое наблюдателем, — стереоскопической моделью (стереомоделью). Стереомодель будет наблюдаться только в пределах перекрытия снимков.
 для наблюдения снимков, полученных с некоторых высот, наиболее используемых при выполнении землеустроительных и кадастровых работ, а также при дистанционном зондировании. При этом примем, что наблюдаются снимки формата 18 х 18 см с продольным перекрытием 60 % с использованием стереоскопа с полуторакратным увеличением.
для наблюдения снимков, полученных с некоторых высот, наиболее используемых при выполнении землеустроительных и кадастровых работ, а также при дистанционном зондировании. При этом примем, что наблюдаются снимки формата 18 х 18 см с продольным перекрытием 60 % с использованием стереоскопа с полуторакратным увеличением.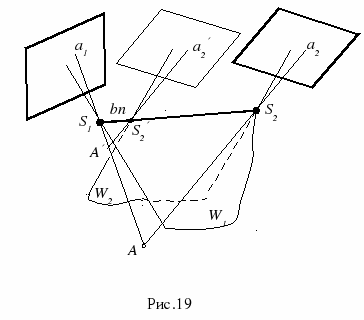

 - угол в главной базисной плоскости левого снимка между осью Z 1 ' и главным лучом связки;
- угол в главной базисной плоскости левого снимка между осью Z 1 ' и главным лучом связки; - угол на левом снимке между осью y 1 и следом плоскости
- угол на левом снимке между осью y 1 и следом плоскости  ;
; - угол в главной базисной плоскости левого снимка между осью Z 2 ' и проекцией главного луча правой связки на главную базисную плоскость левого снимка;
- угол в главной базисной плоскости левого снимка между осью Z 2 ' и проекцией главного луча правой связки на главную базисную плоскость левого снимка; - угол между проекцией главного луча правой связки на главную базисную плоскость левого снимка и главным лучом;
- угол между проекцией главного луча правой связки на главную базисную плоскость левого снимка и главным лучом; - угол на правом снимке между осью y 2 и следом плоскости
- угол на правом снимке между осью y 2 и следом плоскости  .
.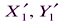 этой системы направлены параллельно соответствующим координатным осям x1, y1 левого снимка (рис. 22), а ось
этой системы направлены параллельно соответствующим координатным осям x1, y1 левого снимка (рис. 22), а ось  совпадает с главным лучом левой связки. Система координат
совпадает с главным лучом левой связки. Система координат 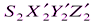 параллельна системе координат
параллельна системе координат  .
. - угол между осью
- угол между осью  и проекцией базиса на плоскость
и проекцией базиса на плоскость  (или элемент ориентирования By);
(или элемент ориентирования By);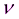 - угол наклона базиса S1S2 относительно плоскости
- угол наклона базиса S1S2 относительно плоскости  (или BZ);
(или BZ); - взаимный продольный угол наклона снимков, составленный осью
- взаимный продольный угол наклона снимков, составленный осью  с проекцией главного луча правой связки на плоскость
с проекцией главного луча правой связки на плоскость  ;
; - взаимный поперечный угол наклона снимков, заключённый между плоскостью
- взаимный поперечный угол наклона снимков, заключённый между плоскостью  и главным лучом правой связки;
и главным лучом правой связки; - взаимный угол поворота снимков, угол на правом снимке между осью y2 и следом
- взаимный угол поворота снимков, угол на правом снимке между осью y2 и следом  плоскости
плоскости 



