
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы взаимного ориентирования пары снимковСодержание книги
Поиск на нашем сайте
При построении модели объекта используется система координат SЛXМYМZМ, у которой начало отсчёта координат расположено в центре проекции левого снимка, т.е. XМSл = YМSл = ZМSл = 0. Следовательно, в системе координат модели объекта из 12 элементов ориентирования пары снимков не равными нулю будут девять аналогично (8). Чтобы отличать их от элементов внешнего ориентирования этих снимков в системе координат объекта, введём индекс "штрих", а базис обозначим буквой b, т.к. его длина задаётся в масштабе модели, и он называется базисом проектирования. wЛ', aЛ', kЛ', b, n', t', wП', aП', kП'. (9) Для облегчения построения модели, расположение пары снимков в системе координат модели задают так, чтобы часть элементов ориентирования (9) стали также равными нулю. С этой целью используют две системы координат модели: базисную и левого снимка. 1. Базисная система координат SЛXМYМZМ (рис. 14, а) названа так потому, что ось ХМ совмещена с базисом проектирования SЛSП, а ось ZМ расположена в главной базисной плоскости VЛ левого снимка, проведённой через базис b и главный оптический луч SЛoЛ. Ось YМ дополняет систему до правой. В базисной системе координат из элементов ориентирования (9) пары снимков равны нулю три угловых элемента ориентирования: wЛ' = n' = t' = 0. В результате в базисной системе координат для пары снимков число элементов ориентирования, не равных нулю, сокращается до шести: aЛ', kЛ', b, wП', aП', kП'. (10) 2. Система координат левого снимка SЛXМYМZМ (рис. 14, б) названа так, потому что она параллельна системе координат SЛxЛyЛzЛ левого снимка. У неё ось ZM совмещена с осью zЛ, а оси XМ и YМ параллельны осям xЛ и yЛ, соответственно. В системе координат левого снимка равны нулю все шесть элементов ориентирования левого снимка: XМSл = YМSл = ZМSл = wЛ' = aЛ' = kЛ' = 0. Следовательно, в этой системе координат из элементов ориентирования (9) не равными нулю будет также шесть:
Как видно, в обеих системах координат модели объекта элементы ориентирования (10) и (11) пары снимков, не равные нулю, состоят из линейного элемента (базиса проектирования b) и пяти угловых элементов. Угловые элементы называют элементами взаимного ориентирования пары снимков. 47) Определение элементов внешнего ориентирования снимков стереопары.
По элементам внешнего ориентирования модели и элементам взаимного ориентирования можно определить элементы внешнего ориентирования снимков стереопары. Линейные элементы внешнего ориентирования снимков
в которых Угловые элементы внешнего ориентирования снимков wi, ai, Ài определяют в следующей последовательности: 1. Сначала получают матрицу преобразования координат i-го снимка
АМ – матрица, в которой элементы aij вычисляют по угловым элементам внешнего ориентирования модели wМ, aМ, ÀМ; Ai’ – матрица, в которой элементы aij вычисляют по угловым элементам взаимного ориентирования i-го снимка wi’, ai’, Ài’. 2. Затем по элементам aij матрицы Ai вычисляют угловые элементы внешнего ориентирования i-го снимка стереопары:
48) Принято различать две системы элементов взаимного ориентирования. В первой системе неподвижным считают базис фотографирования, во второй левый снимок стереопары. Первая система (базисная система, Рис (1.8.)). Элементами взаимного ориентирования в этой системе являются:
Рис. 1.8. Первая система элементов взаимного ориентирования
Началом пространственных координат в первой системе служит центр проекции левого снимка, ось Вторая система (система левого снимка, Рис (1.9.)). Элементами взаимного ориентирования в этой системе являются:
Рис. 1.9. Вторая система элементов взаимного ориентирования
Зная элементы взаимного ориентирования снимков можно найти координаты любой точки модели в фотограмметрической системе координат. 49) Условие, уравнения и элементы взаимного ориентирования снимков.
Рис. 1.10.1
На рис.1.10.1 представлена стереопара снимков Р1 и Р2 в положении, которое они занимали в момент фотографирования. Любая пара соответственных лучей в этом случае пересекается в точке М местности и лежит в плоскости, проходящей через базис фотографирования Очевидно, что в этом случае векторы Как известно из аналитической геометрии, смешанное произведение компланарных векторов равно нулю. Таким образом
Условие компланарности в координатной форме имеет вид:
В уравнении (1.10.2) В дальнейшем эту систему координат будем называть просто системой координат модели. Условие (1.10.2) связывает между собой только направления векторов и выполняется при любых значениях их модулей. Поэтому значение модуля вектора В частном случае величину bx можно выбрать равной 1. При этом направление вектора
Выражение (1.10.2) в этом случае будет иметь вид:
В уравнении (1.10.3)
где i – номер снимка, а А’1 – ортогональная матрица, элементы aij которой являются функциями угловых элементов ориентирования i-го снимка wi’,ai’,Ài’ относительно системы координат модели ОМХМYMZM. В выражении (1.10.3), которое является уравнением взаимного ориентирования в общем виде, куда кроме координат соответственных точек, измеренных на стереопаре снимков, и элементов внутреннего ориентирования входят 8 параметров by, bz, w1’, a1’, À1’, w2’, a2’, À2’, которые определяют угловую ориентацию базиса фотографирования и стереопары снимков относительно системы координат модели ОМХМYMZM. Причем параметры w1’ и w2’ определяют поворот снимков стерепары вокруг оси ХМ, параметры bz, a1’, a2‘ – поворот базиса фотографирования и стереопары снимков вокруг оси YM, а параметры by, À1’, À2 ‘ – поворот базиса фотографирования и стереопары снимков вокруг оси ZM. Однако, из этих 8 параметров только 5 определяют взаимную угловую ориентацию базиса фотографирования и стереопары снимков. Условие (1.10.3) выполняется при любой ориентации системы координат модели ОМХМYMZM. Следовательно, ее можно ориентировать таким образом, чтобы 3 из 8 параметров стали равны нулю. Очевидно, что в общем случае можно сделать равным нулю только один из параметров, входящих в три группы параметров: – w1’, w2’; – bz, a1’, a2‘; – by, À1’, À2’. Таким образом, в качестве элементов взаимного ориентирования можно выбрать любую комбинацию из восьми параметров by, bz, w1’, a1’, À1’, w2’, a2’, À2’, кроме комбинаций, в которые одновременно входят две тройки параметров bz, a1’, a2‘ и by, À1’, À2’, а также пара параметров w1’ и w2’. Рассмотрим наиболее распространенные системы элементов взаимного ориентирования: Система a1’, À1’, w2’, a2’, À2’. Если принять при этом, что by=bz= w1’=0, то уравнение (1.10.3) имеет вид:
Система by, bz, w2’, a2’, À2’. Если при этом принять, что w1’= a1’= À1’ =0, то уравнение (1.10.3) будет иметь вид:
так как
Комментарий. 3 оставшихся из 8 параметров после выбора 5 элементов взаимного ориентирования задают ориентацию системы координат модели ОМХМYMZM. Например, выбрав систему элементов взаимного ориентирования by, bz, w2’, a2’, À2’ и приняв, что w1’= a1’= À1’ =0, мы таким образом задаем систему координат модели ОМХМYMZM, которой параллельны осям x, y, z системы координат первого снимка стереопары S1x1y1z1. В общем случае значения трех параметров можно задавать произвольно. 50) на стереопаре снимков (прямая фотограмметрическая засечка).
Рис.1.7.1 p=x1-x2 – продольный параллакс; q=y1-y2 – поперечный параллакс.

Рис.1.7.2
На рис.1.7.2 показана стереопара снимков Р1 и Р2, на которых точка местности М изобразилась соответственно в точках m1 и m2. Будем считать, что элементы внутреннего и внешнего ориентирования снимков известны. Выведем формулы связи координат точек местности и координат их изображений на стереопаре снимков. Из рис.1.7.2 следует, что векторы Векторы Из рис.1.7.2 следует, что
Так как векторы
где N – скаляр. С учетом (1.7.2) выражение (1.8.1) будет иметь вид
В координатной форме выражение (1.7.3) будет иметь вид
где X1’,Y1’,Z1’ –координаты вектора
Найдем значение N, входящее в выражение (1.7.4). Из рис.1.7.2 следует, что
или с учетом (1.7.2)
Так как векторы
С учетом (1.7.5) выражение (1.7.6) можно представить в виде
или
Выражение (1.7.7) можно представить в виде
или
где
BX, BY, BZ, X1’, Y1’, Z1’, X1’, Y1’, Z1’ – координаты векторов
где i – номер снимка, а
Так как векторы
В координатной форме выражение (1.7.10) с учетом (1.7.8) имеет вид
У коллинеарных векторов отношение их координат равно отношению их модулей, поэтому можно записать, что:
Таким образом, если известны элементы внутреннего и внешнего ориентирования стереопары снимков и измерены на этих снимках координаты сооветственныхточек x1,y1 и x2,y2, то сначала надо определить по одной из формул (1.7.12)-(1.7.14) значение скаляра N, а затем по формуле (1.7.4) вычислить координаты точки местности X,Y,Z. 51)
52) Определение элементов внешнего ориентирования снимка по опорным точкам (обратная фотограмметрическая засечка).
Опорной точкой будем называть точку, опознанную на местности и на снимке, геодезические координаты которой на местности известны. Для определения элементов внешнего ориентирования снимка воспользуемся уравнениями коллинеарности (1.3.12), которые представим в виде
где
или
Если на снимке измерены координаты изображений опорных точек, то каждая опорная точка позволяет составить 2 уравнения (1.5.2),в которых известны значения координат х,у изображения опорной точки в системе координат снимка Sxyz, геодезические координаты опорной точки в системе координат объекта OXYZ и элементы внутреннего ориентирования снимка f,x0,y0. Неизвестными величинами в уравнениях (1.5.2) являются 6 элементов внешнего ориентирования снимка Xs,Ys,Zs,w,a,À. Следовательно, для определения 6 неизвестных элементов внешнего ориентирования снимка достаточно иметь не менее 3 опорных точек. При этом опорные точки на местности не должны располагаться на одной прямой. Если имеются 3 опорные точки, координаты изображений которых на снимке измерены, можно составить систему из 6 уравнений (1.5.2) с 6 неизвестными. В результате решения этой системы уравнений можно найти значения элементов внешнего ориентирования снимка. В связи с тем, что уравнения (1.5.2) не линейны, решение системы уравнений непосредственно достаточно сложно, поэтому систему уравнений (1.5.2) решают методом приближений. Для этого уравнения (1.5.2) приводят к линейному виду, раскладывая их в ряд Тейлора с сохранением членов только первого порядка малости, и переходят к уравнениям поправок.
В уравнениях (1.5.3): dXs, …,dÀ - поправки к приближенным значениям неизвестных элементов внешнего ориентирования снимка Xs0,…,À0; ai,bi – частные производные от уравнений (1.5.2) по соответствующим аргументам (например, коэффициент а4 является частной производной от первого уравнения (1.5.2) по аргументу w,то есть ℓх, ℓу – свободные члены. Значения коэффициентов уравнений (1.5.3) ai,bi вычисляются по известным значениям координат точек снимка и местности х,у и X,Y,Z, известным значениям элементов внутреннего ориентирования снимка f,x0,y0 и приближенным значениям неизвестных Xs0,…,À0. Свободные члены ℓх, ℓу вычисляются по формулам (1.5.2) таким же образом. В результате решения системы уравнений поправок (1.5.3) находят поправки к приближенным значениям неизвестных и вычисляют уточненные значения неизвестных.
По уточненным значениям неизвестных повторно составляют уравнения поправок (1.5.3) и решают полученную систему уравнений. Решения повторяют до тех пор, пока величины поправок, найденные в результате решения, не станут пренебрежительно малыми. В случае если на снимке измерено более трех изображений опорных точек, то для каждой точки составляют уравнения поправок вида:
Решение полученной системы уравнений (1.5.4) производят методом приближений, по методу наименьших квадратов (под условием VTPV=min).
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1597; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.126.51 (0.009 с.) |


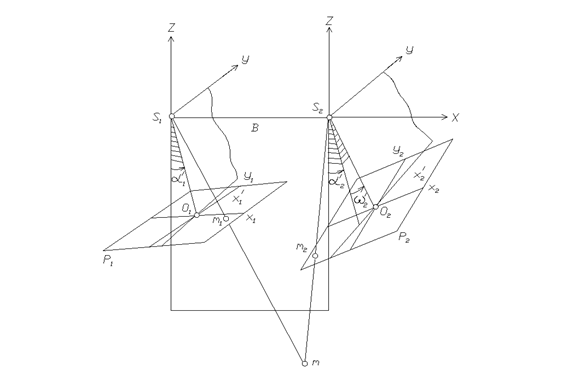
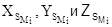 определяют по формулам:
определяют по формулам: ; (1.15.1)
; (1.15.1) ; (1.15.2)
; (1.15.2)
 -- угол в главной базисной плоскости
-- угол в главной базисной плоскости  левого снимка между главным лучом (оптической осью) левой связки
левого снимка между главным лучом (оптической осью) левой связки  и перпендикуляром к базису:
и перпендикуляром к базису: -- угол на левом снимке между осью
-- угол на левом снимке между осью 
 и следом плоскости
и следом плоскости  ;
; -- угол в главной базисной плоскости левого снимка между перпендикуляром к базису и проекцией главного луча (оптической оси) правой связки
-- угол в главной базисной плоскости левого снимка между перпендикуляром к базису и проекцией главного луча (оптической оси) правой связки 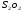 ;
; -- угол между проекцией главного луча (оптической оси) правой связки на базисную плоскость левого снимка и главным лучом
-- угол между проекцией главного луча (оптической оси) правой связки на базисную плоскость левого снимка и главным лучом  -- угол на правом снимке между осью
-- угол на правом снимке между осью  и следом плоскости
и следом плоскости  .
.
 совмещена с базисом, а ось
совмещена с базисом, а ось  находится в главной базисной плоскости левого снимка. Система координат
находится в главной базисной плоскости левого снимка. Система координат  параллельна системе координат
параллельна системе координат 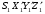 .
. -- угол на левом снимке между осью
-- угол на левом снимке между осью  и следом главной базисной плоскости левого снимка;
и следом главной базисной плоскости левого снимка; -- угол наклона базиса относительно левого снимка;
-- угол наклона базиса относительно левого снимка; -- взаимный продольный угол наклона снимков, составлен осью
-- взаимный продольный угол наклона снимков, составлен осью 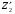 с проекцией главного луча (оптической оси) правой связки на плоскость
с проекцией главного луча (оптической оси) правой связки на плоскость  ;
; -- взаимный поперечный угол наклона снимков, заключенный между плоскостью
-- взаимный поперечный угол наклона снимков, заключенный между плоскостью  -- взаимный угол поворота снимков, угол на правом снимке между осью
-- взаимный угол поворота снимков, угол на правом снимке между осью 
 направлены параллельно соответствующим осям
направлены параллельно соответствующим осям 
 (базисной плоскости).
(базисной плоскости). , лежащие в базисной плоскости, компланарны.
, лежащие в базисной плоскости, компланарны. . (1.10.1)
. (1.10.1) . (1.10.2)
. (1.10.2)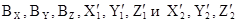 координаты векторов
координаты векторов  можно выбрать произвольно. Направление вектора
можно выбрать произвольно. Направление вектора  , коллинеарного вектору
, коллинеарного вектору 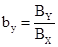 и
и 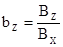 .
. (1.10.3)
(1.10.3) ,
, . (1.10.4)
. (1.10.4) ; (1.10.5)
; (1.10.5) .
.

 определяют соответственно положение точки местности М и центра проекции S1 снимка Р1 относительно начала системы координат объекта OXYZ. Вектор
определяют соответственно положение точки местности М и центра проекции S1 снимка Р1 относительно начала системы координат объекта OXYZ. Вектор  определяет положение центра проекции S2 снимка Р2 относительно центра проекции S1.
определяет положение центра проекции S2 снимка Р2 относительно центра проекции S1.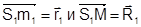 определяют положение точек m1 и М относительно центра проекции S1. Векторы
определяют положение точек m1 и М относительно центра проекции S1. Векторы 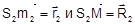 определяют положение точек m2 и М относительно центра проекции S2.
определяют положение точек m2 и М относительно центра проекции S2. (1.7.1)
(1.7.1) коллинеарные, то
коллинеарные, то ; (1.7.2)
; (1.7.2) . (1.7.3)
. (1.7.3)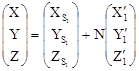 ; (1.7.4)
; (1.7.4) в системе координат объекта OXYZ.
в системе координат объекта OXYZ. .
. ;
; . (1.7.5)
. (1.7.5) . (1.7.6)
. (1.7.6) ;
; . (1.7.7)
. (1.7.7) ;
; ; (1.7.8),
; (1.7.8), - орты, совпадающие с осями координат X,Y,Z системы координат объекта OXYZ;
- орты, совпадающие с осями координат X,Y,Z системы координат объекта OXYZ; ;
;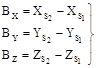 . (1.7.9)
. (1.7.9) коллинеарные (потому что векторы
коллинеарные (потому что векторы  компланарны), значение N можно найти как отношение их модулей, то есть
компланарны), значение N можно найти как отношение их модулей, то есть ; (1.7.10)
; (1.7.10) ; (1.7.11)
; (1.7.11)
 ; (1.5.1)
; (1.5.1)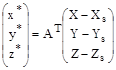 ;
; . (1.5.2)
. (1.5.2) . (1.5.3)
. (1.5.3) );
);
 ; (1.5.4)
; (1.5.4)


