
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условные математические обозначенияСодержание книги
Поиск на нашем сайте
УДК 621.59:53:519.8 ББК 22.311в6
© Январев И.А., 2006 © Омский государственный технический университет, 2006
ВВЕДЕНИЕ
Невозможно избавиться от ощущения, что математические формулы существуют независимо от нас и обладают собственным разумом, что они мудрее нас, мудрее даже тех, кто их открыл, и что мы извлекаем из них больше, чем первоначально было заложено. Г. Герц
Практически во всех отраслях промышленности – в криогенной технике, химическом и нефтехимическом производстве, при добыче, хранении и транспортировке нефти и газа, в энергетике и на транспорте, легкой и пищевой промышленности, на предприятиях машиностроительного комплекса, металлургии и других эксплуатируются установки различного назначения, энергоемкость и безопасность функционирования которых во многом зависят от эффективности реализуемых физических процессов. В свою очередь применение высококачественных математических моделей позволяет проводить исследование этих процессов при неизмеримо меньших затратах, чем натурные исследования на реальных агрегатах, стендах или физических моделях. С помощью математических моделей можно еще на стадии проектирования найти оптимальное конструктивное оформление агрегата, технологических аппаратов и выбрать оптимальные режимные параметры их работы. Математическое моделирование физических процессов криогенных, компрессорных, холодильных, энергетических и технологических установок предполагает использование комплексного подхода при рассмотрении таких процессов как движение жидкостей и газов, процессы внешнего и внутреннего теплообмена, различные виды массообмена. Для описания физических процессов используется формально-логический аппарат математики. Обычно это системы дифференциальных, интегральных либо интегрально-дифференциальных уравнений. В математическую формулировку задачи входят также начальные и граничные условия, геометрические и физические параметры. Математическое моделирование как метод исследования в настоящее время получил самое широкое распространение. Сочетая достоинства теоретических и экспериментальных подходов, математическое моделирование позволяет исследовать явления, не доступные физическому моделированию, обобщать результаты на основе многократного использования модели, а также делать прогнозы о возможном поведении процесса при изменении определяющих параметров (проведение численного эксперимента). Поэтому при подготовке инженеров по специальностям 140401 «Техника и физика низких температур», 150801 «Вакуумная и компрессорная техника физических установок», 140104 «Промышленная теплоэнергетика», 240801 «Машины и аппараты химических производств» для различных отраслей промышленности важное значение имеет изучение физических процессов криогенных, компрессорных, холодильных, энергетических и технологических установок и подходов при создании их качественных математических моделей. Ядром математического моделирования является понятие математической модели(ММ), которая дает исследователю возможность сконцентрировать внимание на доминирующих факторах объекта (явления, процесса), исключая несущественные путем принятия соответствующих допущений. Описание объекта с необходимой точностью при сохранении качественного соответствия обеспечивает применение численного моделирования на различных по степени детализации уровнях. Основу математической модели, в свою очередь, составляет ее математическое описание, которое, являясь отражением физической сущности объекта (процесса), выражается в функциональном соотношении между входными Х, выходными Y и управляющими U параметрами. При составлении математического описания наиболее распространенными являются детерминированный и стохастический подходы. Детерминированное описание строится на основе анализа физической и химической сущности моделируемого объекта и состоит из фундаментальных закономерностей гидродинамики потоков, термодинамики, химической кинетики, законов сохранения массы и энергии. Общая стратегия построения математических моделей отдельных объектов (процессов) в этом случае предполагает получение зависимостей для потоков количества движения, энергии и массы между отдельными элементами системы и окружающей средой. Аналитическое решение получаемых уравнений, однако, для большинства реальных объектов в силу их сложности весьма затруднено, а зачастую и невозможно. Поэтому на практике прибегают либо к упрощению исходной системы путем исключения членов малой значимости с последующим получением грубых моделей ручного счета, либо, особенно при использовании ЭВМ, к методам численного моделирования. Кроме того, если описываемые объекты сложны и не поддаются декомпозиции, а также в случаях недостаточной информации о протекающих в них процессах, возможно, имеющих случайный характер, может быть использован стохастический подход. Стохастическое описание основано на статистическо-вероятных соотношениях между входными и выходными параметрами объекта. Эти соотношения отражают также нестационарность процесса. Поскольку для большинства рассматриваемых объектов свойственна детерминированно-стохастическая природа, более обоснованным будет описание, включающее обе эти составляющие.
Понятие ММ Математическое моделирование – процесс создания модели и оперирование ею с целью получения сведений о реальном объекте [6]. Альтернативой математического моделирования является физическое макетирование, но у математического моделирования есть ряд преимуществ: меньшие сроки на подготовку анализа; значительно меньшая материалоемкость, особенно при проектировании крупногабаритных объектов; возможность выполнения экспериментов на критических режимах, которые привели бы к разрушению физического макета, и др. Математическая модель (ММ) – совокупность математических объектов (чисел, символов, множеств и т. д.) и связей между ними, отражающих важнейшие для проектировщика свойства проектируемого технического объекта. Математический метод – совокупность правил и допущений, отраженная в последовательности действий над математическими объектами и направленная на получение некоторого решения.
Требования к ММ Универсальность – степень применимости ММ к анализу более или менее многочисленной группы объектов определенного типа. Точность – степень совпадения значений параметров реального объекта Погрешность может быть абсолютной Адекватность – способность отражать заданные свойства объекта с погрешностью не выше заданной Экономичность – характеризуется затратами вычислительных ресурсов (время расчета, память), необходимых для реализации модели.
Классификация ММ По характеру отражаемых свойств: – функциональные ММ – для отображения физических или информационных процессов; – структурные ММ – для отображения структурных свойств объекта (топологические – состав и взаимосвязи элементов, геометрические – расположение и форма). По принадлежности к уровню иерархии: – микро-ММ – для отображения физических процессов, протекающих в непрерывном пространстве и времени; – макро-ММ – для отображения физических процессов протекающих в непрерывном времени или вдоль одной из координат, а также структурных свойств объекта (для объектов сложной структуры). – мета-ММ - описывают достаточно сложные совокупности (системы) объектов. По степени детализации описания: – полные ММ включают фазовые переменные, характеризующие состояние всех межэлементных связей; – грубые ММ отображаются основные межэлементные связи. По способу представления свойств объекта: – аналитические ММ – явные выражения выходных параметров Y как функции f от входных Х и внутренних Q – Y=f(X,Q); – алгоритмические ММ – выражают связи выходных параметров с внутренними и входными в форме алгоритма L – Y=L(X,Q). По способу получения ММ: – теоретические ММ – как результат исследований внутренних процессов и закономерностей объекта. – эмпирические ММ – в результате изучения внешних проявлений свойств объекта.
Библиографический список
1. Андерсон Д. Вычислительная гидромеханика и теплообмен: В 2 т.: Пер. с англ. /Д. Андерсон, Дж. Таннехилл, Р. Плетчер. М.: Мир, 1990. 728 с. 2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: Учеб. пособие / Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. М.: Наука, 1987. 600с. 3. Белова Д.А., Кузин Р.Е. Применение ЭВМ для анализа и синтеза автоматических систем управления / Д.А. Белова, Р.Е. Кузин М.: Энергия, 1979. 264 с. 4. Драйнер Н., Смит Г. Прикладной регрессионный анализ / Н. Драйнер, Г.Смит. М., 1973. 336 с. 5. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача: Учебник для вузов. 3-е изд., перераб. и доп. М.: Энергия, 1975. 488 с. 6. Норенков И.П. Основы автоматизированного проектирования: Учеб. для вузов. М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. 360 с. 7. Каплун А.Б., Морозов Е.М., Олферьева М.А. ANSYS в руках инженера: Практ. руководство. 2-е изд., испр. М.: Едиториал УРСС, 2004. 272 с. 8. Кафаров В.В. Методы кибернетики в химии и химической технологии. 4-е изд., перераб. и доп. М.: Химия, 1985. 448 с. 9. Каханер Д., Моулер К., Нэш С. Численные методы и математическое обеспечение: Пер. с англ. / Д. Каханер, К. Моулер, С. Нэш М.: Мир, 1998. 575 с. 10. Математическое моделирование теплообменных процессов компрессорных, холодильных, энергетических и технологических установок: Метод. указания по проведению лабораторных работ / Сост. И.А. Январев Омск: Изд-во ОмГТУ, 2006. 64 с. 11. Реклейтис Г. Оптимизация в технике: Пер. с англ. / Г. Реклейтис, А.Рейнвиндран, К. Рэгсдел. М.: Мир, 1986. 443 с. 12. Патанкар С.В. Численное решение задач теплопроводности и конвективного теплообмена при течениях в каналах / Пер. с англ. Е.В. Калабина; под ред. Г.Г. Янькова. М.: МЭИ, 2003. 312 с. 13. Самарский А.А., Вабищевич П.Н. Вычислительная теплопередача. М.: Едиториал УРСС, 2003. 784 c. 14. Статюха Г.А. Автоматизированное проектирование химико-технологических систем. К.: Выща шк. Головное изд-во, 1989. 400 с. 15. Турчак Л.И. Основы численных методов. М.: Наука, 1987. 320 с. 16. Шимкович Д.Г. Расчет конструкций в MSC/NASTRAN for Windows. – М.:ДМК Пресс, 2001. 448 с. 17. Январев И.А. Теплообменное оборудование и системы охлаждения компрессорных, холодильных и технологических установок. Учеб. пособие. / И.А. Январев. В.Л. Юша, В.П. Парфенов, В.А. Максименко, А.Д. Ваняшов. Омск: Изд-во ОмГТУ, 2005. 450 с. 18. Янишевская А.Г., Пергун И.Н. Использование программного комплекса ANSYS при расчетах тепловых процессов в машиностроении: Учеб. пособие. Омск: Изд-во ОмГТУ, 2001. 96 с.
СОДЕРЖАНИЕ
Редактор Т.А. Жирнова ИД № 06039 от 12.10.01 Сводный темплан 2006 г. Подписано в печать 25.07.06. Формат 60х84 1/16. Бумага офсетная. Отпечатано на дупликаторе. Усл. печ. л. 4,5. Уч.- изд. л. 4,5. Тираж Заказ.
Издательство ОмГТУ. 644050, Омск, пр. Мира, 11. Типография ОмГТУ.
УДК 621.59:53:519.8 ББК 22.311в6
© Январев И.А., 2006 © Омский государственный технический университет, 2006
ВВЕДЕНИЕ
Невозможно избавиться от ощущения, что математические формулы существуют независимо от нас и обладают собственным разумом, что они мудрее нас, мудрее даже тех, кто их открыл, и что мы извлекаем из них больше, чем первоначально было заложено. Г. Герц
Практически во всех отраслях промышленности – в криогенной технике, химическом и нефтехимическом производстве, при добыче, хранении и транспортировке нефти и газа, в энергетике и на транспорте, легкой и пищевой промышленности, на предприятиях машиностроительного комплекса, металлургии и других эксплуатируются установки различного назначения, энергоемкость и безопасность функционирования которых во многом зависят от эффективности реализуемых физических процессов. В свою очередь применение высококачественных математических моделей позволяет проводить исследование этих процессов при неизмеримо меньших затратах, чем натурные исследования на реальных агрегатах, стендах или физических моделях. С помощью математических моделей можно еще на стадии проектирования найти оптимальное конструктивное оформление агрегата, технологических аппаратов и выбрать оптимальные режимные параметры их работы. Математическое моделирование физических процессов криогенных, компрессорных, холодильных, энергетических и технологических установок предполагает использование комплексного подхода при рассмотрении таких процессов как движение жидкостей и газов, процессы внешнего и внутреннего теплообмена, различные виды массообмена. Для описания физических процессов используется формально-логический аппарат математики. Обычно это системы дифференциальных, интегральных либо интегрально-дифференциальных уравнений. В математическую формулировку задачи входят также начальные и граничные условия, геометрические и физические параметры. Математическое моделирование как метод исследования в настоящее время получил самое широкое распространение. Сочетая достоинства теоретических и экспериментальных подходов, математическое моделирование позволяет исследовать явления, не доступные физическому моделированию, обобщать результаты на основе многократного использования модели, а также делать прогнозы о возможном поведении процесса при изменении определяющих параметров (проведение численного эксперимента). Поэтому при подготовке инженеров по специальностям 140401 «Техника и физика низких температур», 150801 «Вакуумная и компрессорная техника физических установок», 140104 «Промышленная теплоэнергетика», 240801 «Машины и аппараты химических производств» для различных отраслей промышленности важное значение имеет изучение физических процессов криогенных, компрессорных, холодильных, энергетических и технологических установок и подходов при создании их качественных математических моделей. Ядром математического моделирования является понятие математической модели(ММ), которая дает исследователю возможность сконцентрировать внимание на доминирующих факторах объекта (явления, процесса), исключая несущественные путем принятия соответствующих допущений. Описание объекта с необходимой точностью при сохранении качественного соответствия обеспечивает применение численного моделирования на различных по степени детализации уровнях. Основу математической модели, в свою очередь, составляет ее математическое описание, которое, являясь отражением физической сущности объекта (процесса), выражается в функциональном соотношении между входными Х, выходными Y и управляющими U параметрами. При составлении математического описания наиболее распространенными являются детерминированный и стохастический подходы. Детерминированное описание строится на основе анализа физической и химической сущности моделируемого объекта и состоит из фундаментальных закономерностей гидродинамики потоков, термодинамики, химической кинетики, законов сохранения массы и энергии. Общая стратегия построения математических моделей отдельных объектов (процессов) в этом случае предполагает получение зависимостей для потоков количества движения, энергии и массы между отдельными элементами системы и окружающей средой. Аналитическое решение получаемых уравнений, однако, для большинства реальных объектов в силу их сложности весьма затруднено, а зачастую и невозможно. Поэтому на практике прибегают либо к упрощению исходной системы путем исключения членов малой значимости с последующим получением грубых моделей ручного счета, либо, особенно при использовании ЭВМ, к методам численного моделирования. Кроме того, если описываемые объекты сложны и не поддаются декомпозиции, а также в случаях недостаточной информации о протекающих в них процессах, возможно, имеющих случайный характер, может быть использован стохастический подход. Стохастическое описание основано на статистическо-вероятных соотношениях между входными и выходными параметрами объекта. Эти соотношения отражают также нестационарность процесса. Поскольку для большинства рассматриваемых объектов свойственна детерминированно-стохастическая природа, более обоснованным будет описание, включающее обе эти составляющие.
Условные математические обозначения
1. СКАЛЯР (от лат. scalaris - ступенчатый) (скалярная величина), величина, каждое значение которой (в отличие от вектора) может быть выражено одним (действительным) числом (тензор нулевого порядка), вследствие чего совокупность значений скаляра можно изобразить на линейной шкале (scale – отсюда название). Длина, площадь, время, температура и т. д. - скалярные величины. 2. Скалярная функция Ф (x,y,z) – ставит в соответствие каждому набору значений скалярных аргументов x,y,z единственное действительное значение Ф (скаляр). 3. Векторная функция 4. Оператор
4.1. Градиент скалярной функции Ф – это векторная функция (тензор первого порядка - вектор), составляющие элементы значения которой есть частные производные
4.2. Градиент векторной функции
4.3. Дивергенция векторной функции
4.4. Ротор векторной функции
5. Оператор
Этот оператор может быть применен к скалярным Ф и векторным
5.1. Оператор Лапласа скалярной функции Ф это скалярная величина
5.2. Оператор Лапласа векторной функции
6. Полная производная скалярной функции Ф(x,y,z) по времени t – это скорость ее изменения по отношению к параметру t, если координаты есть функции от времени x=x(t), y=y(t), z=z(t), а
7. Полная (субстанциональная) производная скалярной функции Ф(x,y,z,t) когда Ф явно зависит от t:
8. Полная (субстанциональная) производная векторной функции
9. Прочие обозначения:
Е – энергия, Дж; F – площадь, м2; G – массовый расход, кг/с; H – энтальпия, Дж; k – коэффициент теплопередачи, Вт/(м2 К); L – работа, Дж; N – мощность, Вт; Р – давление, Па; Q – количество теплоты, Дж; q – удельный тепловой поток, Вт/ м2; R – удельная газовая постоянная, Дж/(кг К); Re – число Рейнольдса, St – число Стантона; Т – температура, К; t – время, с; U – внутренняя энергия, Дж; V – объём, м3; x, y, z – декартовы координаты;
α – коэффициент теплоотдачи, Вт/(м2 К); η – коэффициент полезного действия (КПД); λ – теплопроводность, Вт/(м К); μ – динамическая вязкость, Па с; ν – кинематическая вязкость, м2/с; ξ – коэффициент потерь на трение; π – степень повышения (понижения) давления; ρ – плотность, кг/м3;
1. Метод математического моделирования. Понятие математической модели
Понятие ММ Математическое моделирование – процесс создания модели и оперирование ею с целью получения сведений о реальном объекте [6]. Альтернативой математического моделирования является физическое макетирование, но у математического моделирования есть ряд преимуществ: меньшие сроки на подготовку анализа; значительно меньшая материалоемкость, особенно при проектировании крупногабаритных объектов; возможность выполнения экспериментов на критических режимах, которые привели бы к разрушению физического макета, и др. Математическая модель (ММ) – совокупность математических объектов (чисел, символов, множеств и т. д.) и связей между ними, отражающих важнейшие для проектировщика свойства проектируемого технического объекта. Математический метод – совокупность правил и допущений, отраженная в последовательности действий над математическими объектами и направленная на получение некоторого решения.
Требования к ММ Универсальность – степень применимости ММ к анализу более или менее многочисленной группы объектов определенного типа. Точность – степень совпадения значений параметров реального объекта Погрешность может быть абсолютной Адекватность – способность отражать заданные свойства объекта с погрешностью не выше заданной Экономичность – характеризуется затратами вычислительных ресурсов (время расчета, память), необходимых для реализации модели.
Классификация ММ По характеру отражаемых свойств: – функциональные ММ – для отображения физических или информационных процессов; – структурные ММ – для отображения структурных свойств объекта (топологические – состав и взаимосвязи элементов, геометрические – расположение и форма). По принадлежности к уровню иерархии: – микро-ММ – для отображения физических процессов, протекающих в непрерывном пространстве и времени; – макро-ММ – для отображения физических процессов протекающих в непрерывном времени или вдоль одной из координат, а также структурных свойств объекта (для объектов сложной структуры). – мета-ММ - описывают достаточно сложные совокупности (системы) объектов. По степени детализации описания: – полные ММ включают фазовые переменные, характеризующие состояние всех межэлементных связей; – грубые ММ отображаются основные межэлементные связи. По способу представления свойств объекта: – аналитические ММ – явные выражения выходных параметров Y как функции f от входных Х и внутренних Q – Y=f(X,Q); – алгоритмические ММ – выражают связи выходных параметров с внутренними и входными в форме алгоритма L – Y=L(X,Q). По способу получения ММ: – теоретические ММ – как результат исследований внутренних процессов и закономерностей объекта. – эмпирические ММ – в результате изучения внешних проявлений свойств объекта.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.58.68 (0.009 с.) |

 и значений тех же параметров, рассчитанных с помощью ММ
и значений тех же параметров, рассчитанных с помощью ММ  . Точность ММ характеризуется количественной (погрешность) и качественной (адекватность) оценкой.
. Точность ММ характеризуется количественной (погрешность) и качественной (адекватность) оценкой. или относительной
или относительной  .
. .
. (x,y,z) – ставит в соответствие каждому набору значений скалярных аргументов x,y,z вектор
(x,y,z) – ставит в соответствие каждому набору значений скалярных аргументов x,y,z вектор  , называемый градиент Набла, или оператор Набла, представляет собой частную производную для некоторого параметра относительно всех направлений в выбранной системе координат. В декартовых координатах
, называемый градиент Набла, или оператор Набла, представляет собой частную производную для некоторого параметра относительно всех направлений в выбранной системе координат. В декартовых координатах 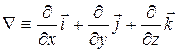 , где
, где  .
.
 .
. .
. (или
(или  , иногда обозначается ∆), называемый оператором Лапласа (лапласиан), и выражается в декартовых прямоугольных координатах формулой:
, иногда обозначается ∆), называемый оператором Лапласа (лапласиан), и выражается в декартовых прямоугольных координатах формулой: .
. ,
, отличается от
отличается от 
 .
. .
.

 скорости их изменения во времени:
скорости их изменения во времени: .
. .
. .
. – удельная массовая теплоемкость при постоянном давлении, Дж/(кг К);
– удельная массовая теплоемкость при постоянном давлении, Дж/(кг К);


