
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения с частными производными и краевыми условиями (краевые задачи)
Для уравнений эллиптического типа Исследования стационарных процессов различной физической природы (теплопроводность и др.) часто приводят к уравнениям эллиптического типа
где 1. Первая краевая задача. На контуре Г, ограничивающем область G (рис. 4), задана непрерывная функция
Рис. 4. Область исследования
2. Вторая краевая задача. На контуре Г, ограничивающем область G (рис. 4), задана непрерывная функция 3. Третья краевая задача. На контуре Г, ограничивающем область G (рис. 4), задана непрерывная функция Третья краевая задача может быть рассмотрена как общая. Действительно, при
Уравнения Лапласа в конечных разностях
Для получения конечно-разностного уравнения, соответствующего уравнению Лапласа (частный случай уравнения эллиптического типа)
достаточно, выбрав шаг h>0, заменить производные отношениями конечных разностей по формулам:
Тогда после преобразования будем иметь
Применение метода сеток для решения задачи Дирихле
Идея метода сеток (метода конечных разностей) для численного решения краевых задач для двумерных дифференциальных уравнений заключается: 1) в плоскости G, в которой разыскивается решение, строится сеточная область
2) заданное дифференциальное уравнение заменяется в узлах построенной сетки соответствующим конечно-разностным уравнением; 3) на основании граничных условий устанавливаются значения искомого решения в граничных узлах области Решив полученную систему конечно-разностных уравнений (т.е. систему алгебраических уравнений с большим числом неизвестных), мы найдем значения искомой функции в узлах сетки. Сеточная область может состоять из квадратных, прямоугольных, треугольных и других клеток. От выбора основного размера клетки h зависит величина погрешности. Обычно задача решается сначала при большом значении h (малом числе клеток), а затем после грубого решения переходят к более мелкой сетке или во всей рассматриваемой области, или в какой-нибудь ее перспективной части. Покажем применение метода сеток для построения решения задачи Дирихле
где Для простоты рассмотрим лишь случай квадратной сетки. Будем предполагать также, что область G ограничена простым замкнутым кусочно-гладким контуром Г. Выбрав шаг h, построим квадратную сетку Узлы сетки
Рис. 5. Узлы сетки Граничный узел сетки
Относительно сетки Значение искомой функции и=и(х,у) в точках
где В граничных узлах первого рода где B – ближайшая к Система (46) является неоднородной системой, причем число неизвестных (т.е. число внутренних узлов сетки) равно числу уравнений. Решив систему (46), получим приближенные значения искомой функции и=и(х,у) в узлах сеточной области Если число узлов сетки
Для уравнений параболического типа
В качестве примера уравнения параболического типа рассмотрим уравнение теплопроводности для однородного стержня 0 ≤ x ≤ l
где u=u(х,t) – температура и t – время. В дальнейшем для простоты будем полагать а= 1 (к такому случаю всегда можно прийти путем введения нового времени τ=a2t). Итак, рассмотрим уравнение
Пусть в начальный момент времени t=0 задано распределение температуры u(x,0)=f(x) и законы изменения температуры в зависимости от времени (тепловые режимы) на концах стержня х=0 и x=l: u(0,t)=φ(t), u(l,t)=ψ(t). Требуется найти распределение температуры u=u(х,t) вдоль стержня в любой момент времени t. Решим эту смешанную задачу методом сеток. Для этого рассмотрим пространственно-временную систему координат (х,t) (рис. 6).
Рис. 6. Прямоугольная сетка
В полуполосе t ≥0, 0 ≤ x ≤ l построим прямоугольную сетку x=ih (i=0, 1,…, n), t=jk (j=0, 1, 2,…), где h=l/n (n – целое) – шаг вдоль оси Ох и k2=σh2 – шаг вдоль оси Ot (σ – постоянная), вообще говоря, различны. Величина σ будет выбрана ниже. Введя обозначения xi =ih, tj =jk, uij=u(xi, tj) и заменяя уравнение (49) конечно-разностным уравнением, получим:
Отсюда
ui,j+1= σ ui-1,j+(1-2σ)uij+ σ ui+1,j. (51)
Из рассмотрения формулы (51) ясно, что зная значения функции u(х,t) в точках j -го слоя t=jk, с помощью этой формулы можно вычислить значения u(х,t) в точках следующего (j+1) -го слоя t=(j+1)k (риc. 7). При вычислении пользуются четырьмя соседними узлами – явная схема вида (рис. 7).
Рис. 7. Явная схема с использованием одного предыдущего слоя j
Таким образом, исходя из начального слоя t=0, значения u(х,t) для которого определяются из начального условия u(xi,0)=f(xi), (i=0, 1,…, n), и используя значения функции u(х,t) в крайних узлах (0, tj), (1, tj) (j=0, 1, 2,…), определяемые граничными условиями u(0,tj)= φ(tj), u(l,tj)= ψ(tj), по формуле (51) последовательно вычисляем: u(xi,t1), u(xi,t2), u(xi,t3),… (i=0, 1,…, n), т. е. находим значения искомой функции u(х,t) во всех узлах полуполосы.
Остается разумно выбрать величину σ. При этом будем исходить из требования, чтобы ошибка при замене дифференциального уравнения (49) конечно-разностным уравнением (50) была наименьшей. Введем обозначения:
где Lh[u] – конечно-разностный оператор, соответствующий дифференциальному оператору L[u]. Разность Rh[u]=Lh[u]-L[и], называемая ошибкой аппроксимации, есть погрешность, которая получается при замене оператора L[и] оператором Lh[u]. Для Lh[u] можно записать
Тогда выберем число σ так, чтобы первая скобка формулы (52) обратилась в нуль, т. е. положим σ/2=1/12 и, следовательно, σ=1/6. При этом значении σ будем иметь
При выполнении равенства Rh[u]=Lh[u] при таком выборе σ для погрешности Rh[u] получаем оценку Rh[u]=О(h4), тогда как при другом выборе числа σ имеем Rh[u]=О(h2). В этом смысле значение σ =1/6 является для расчетной схемы 1 наилучшим. Соответствующая расчетная формула (51) при таком выборе σ окончательно принимает вид
ui,j+1=1/6(ui-1,j+4uij+ui+1,j). (54)
Отметим, что оценка ошибки аппроксимации Rh[u] в общем случае для граничных узлов (xi, tj) не годится.
Для уравнений гиперболического типа
Рассмотрим простейшее уравнение гиперболического типа:
Будем искать решение уравнения (55) при заданных начальных и краевых условиях:
u(х,0)=f(х), ut(х,0)=F(х) (0 ≤ х ≤ l) (56)
u(0,t)= φ(t), u(l,t)= ψ(t) (0 ≤ t < ∞). (57)
Как и в случае параболического уравнения, решая задачу методом сеток, покроем полуполосу (0 ≤ х ≤ l), (0 ≤ t <∞) прямоугольной сеткой xi=ih (i=0, 1,…, n), tj=jk (j=0, 1, 2,…), где ∆xi=xi+1-xi=h=l/n (n – целое) и ∆tj=tj+1-tj=k. На сетке xi, tj приближенно заменим дифференциальное уравнение (55) соответствующим конечно-разностным уравнением. Пользуясь симметричными формулами для производных, будем иметь
При k=h/а уравнение (58) упрощается и принимает вид
ui,j+1=ui+1,j+ui-1,j-ui,j-1 . (59)
Из уравнения (59) видно, что для получения значений u(х,t) в (j+1) -м слое используются значения u(х,t) в двух предыдущих слоях: j -м и (j-1)- м (рис. 8).
Рис. 8. Схема с использованием двух предыдущих слоев j-1 и j
Для начала вычисления по формуле (59) также необходимо знать значения u(х,t) на двух слоях, в то время как начальные условия (56) задают нам значения u(х,t) лишь на нулевом слое j=0. Однако, используя начальные условия, можно определить значения u(х,t) на фиктивном слое с номером j=-1. Для этого заменим производную во втором начальном условии конечно-разностным отношением.
где Fi=F(Xi). Отсюда ui,-1=uio –kFi. Теперь, зная значения u(х,t) на слое j=-1, определяемые с помощью формулы (60), можно начать вычисления. Краевые условия (57) используются для получения значений uoj и unj. Вместо определения значений u(х,t) на слое j=-1 можно вычислить значения u(х,t) на слое j=1. Это достигается, например, с помощью формулы Тейлора:
Учитывая вид уравнения (55), а также из начальных условий (56) предполагая, что
Очевидно формулу (62) целесообразно применять в том случае, когда функция f(х) задана аналитическим выражением.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.17.46 (0.083 с.) |
 , (42)
, (42) – непрерывные функции. Для этих уравнений обычно ставятся лишь краевые задачи, так как задачи Коши для эллиптического уравнения может быть некорректной. Наиболее часто встречаются следующие краевые задачи:
– непрерывные функции. Для этих уравнений обычно ставятся лишь краевые задачи, так как задачи Коши для эллиптического уравнения может быть некорректной. Наиболее часто встречаются следующие краевые задачи: . Требуется найти функцию
. Требуется найти функцию 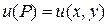 , удовлетворяющую внутри G уравнению (42) и принимающую на границе заданные значения
, удовлетворяющую внутри G уравнению (42) и принимающую на границе заданные значения  , т.е. должны быть выполнены условия
, т.е. должны быть выполнены условия  при
при  ;
; 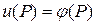 при
при 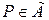 .
.
 . Требуется найти функцию
. Требуется найти функцию  при
при  . Требуется найти функцию
. Требуется найти функцию  при
при 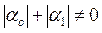 .
. и
и  получаем первую краевую задачу, а при
получаем первую краевую задачу, а при  и
и  получаем вторую краевую задача. Если область G ограничена, то соответствующая краевая задача называется внутренней, а в противном случае – внешней. Для уравнения Лапласа
получаем вторую краевую задача. Если область G ограничена, то соответствующая краевая задача называется внутренней, а в противном случае – внешней. Для уравнения Лапласа  первая краевая задача называется задачей Дирихле, вторая – задачей Неймана и третья – смешанной краевой задачей.
первая краевая задача называется задачей Дирихле, вторая – задачей Неймана и третья – смешанной краевой задачей. , (43)
, (43)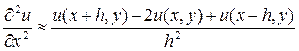 и
и  .
. . (44)
. (44)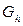 , состоящее из одинаковых ячеек и приближающая данную область G;
, состоящее из одинаковых ячеек и приближающая данную область G;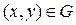 и
и 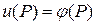 при
при  – заданная непрерывная функция.
– заданная непрерывная функция. ,
,  с таким расчетом, чтобы узлы (
с таким расчетом, чтобы узлы ( ,
,  ) сетки
) сетки  или принадлежали области G, или отстояли от ее границы Г на расстояние меньше, чем h.
или принадлежали области G, или отстояли от ее границы Г на расстояние меньше, чем h.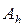 называется внутренним, если он принадлежит области G, а все четыре соседних с ним узла – множеству
называется внутренним, если он принадлежит области G, а все четыре соседних с ним узла – множеству  и
и  сетки
сетки 
 выбранной так, чтобы ее геометрическая граница
выбранной так, чтобы ее геометрическая граница  , возможно ближе примыкала к границе Г области G. Заметим, что узловые точки контура
, возможно ближе примыкала к границе Г области G. Заметим, что узловые точки контура  обозначим через
обозначим через  . Следуя общей схеме, для каждой внутренней точки
. Следуя общей схеме, для каждой внутренней точки 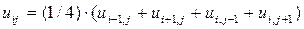 , (46)
, (46) – расчетные точки.
– расчетные точки. ,
, , последовательные приближения
, последовательные приближения  для внутренних узлов
для внутренних узлов  (k=1,2,…). (47)
(k=1,2,…). (47) , (48)
, (48)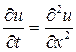 . (49)
. (49)
 . (50)
. (50)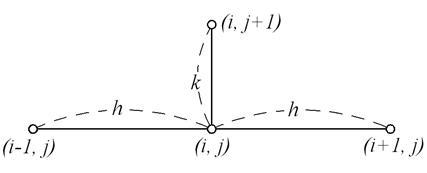
 , Lh[u]=1/h2[(ui+1,j –2uij+ui-1,j)-1/ σ(ui,j+1 –uij)],
, Lh[u]=1/h2[(ui+1,j –2uij+ui-1,j)-1/ σ(ui,j+1 –uij)], . (52)
. (52)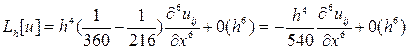 . (53)
. (53) . (55)
. (55) , (58)
, (58)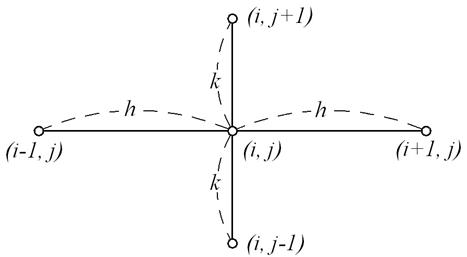
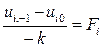 , или ui,-1=uio –kFi, (60)
, или ui,-1=uio –kFi, (60)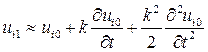 . (61)
. (61) , получив
, получив 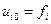 ,
,  ,
, 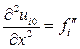 , перепишем формулу (61) в другом виде, а именно:
, перепишем формулу (61) в другом виде, а именно: . (62)
. (62)


