
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая характеристика микромоделей
Математической моделью технического объекта на микроуровне является система дифференциальных уравнений в частных производных, описывающая процессы в непрерывной среде и времени с заданными краевыми условиями. Независимые переменные: x, y, z, t. Зависимые (фазовые) переменные, характеризующие физическое состояние объекта (их изменения во времени – переходные процессы): для механической системы – скорость, сила, для гидравлической системы – давление, расход, для тепловой системы – температура, тепловой поток. Уравнения: интегральные, интегро-дифференциальные, дифференциальные в частных производных (ДУЧП) (уравнения Ламе для механики упругих сред; уравнения Навье–Стокса для гидравлики; уравнения теплопроводности для термодинамики и т. д.). Результат: поля фазовых переменных. В частности, при моделировании процессов, протекающих в различных технических объектах, среди основных можно выделить процессы движения и теплообмена. Наиболее общими уравнениями, описывающими процессы движения, являются уравнения Навье-Стокса, которые при определении полной производной
где Процессы теплообмена (переноса теплоты) связаны с обменом внутренней энергией между элементами исследуемого объекта. Поэтому они описываются в общем случае уравнением переноса внутренней энергии (т.е. без учета изменения кинетической и потенциальной ее составляющих). В самом общем виде уравнение энергии для изобарического (при постоянном давлении) процесса переноса теплоты можно записать [5] как
где i=i(Т,p) – энтальпия единицы объема; Т – температура;
Теплообмен может осуществляться тремя способами: теплопроводностью, конвекцией и тепловым излучением: 1) теплопроводность –перенос, определяемый взаимодействием микрочастиц соприкасающихся тел; 2) конвекция –перенос, обусловленный пространственным перемещением вещества. Наблюдается в движущихся средах (жидкости, газы); 3) излучение – перенос энергии в виде электромагнитных волн. Во многих прикладных задачах процесс переноса тепла осуществляется различными способами (сложный теплообмен). При описании конвективных переносов необходимо учитывать процессы теплопроводности между отдельными частями сплошной среды (тепло- и массоперенос). Радиационный теплообмен (излучение) может осложняться теплопроводностью, конвекцией и т. д. Примером такого сложного теплообмена могут служить процессы при фазовых превращениях, химических реакциях. При рассмотрении процессов теплопередачи в твердых телах большое значение могут приобретать эффекты, связанные с расширением тел при повышении температуры. Если при переносе теплоты для локального (местного) значения плотности теплового потока учитывать только теплопроводность и конвекцию
где Если
Уравнения (1–3) имеют множество решений. Для получения единственного решения необходимо задавать краевые условия (сведения об искомых непрерывных функциях на границах рассматриваемых областей – граничные условия, а вслучае нестационарных задач – значения этих же функций в начальный момент времени – начальные условия). Исходное дифференциальное уравнение в частных производных вместе с краевыми условиями носит название дифференциальной краевой задачи (с начальными условиями – задачей Коши) и представляет собой ММ исследуемого объекта.
Граничные условия в краевых задачах могут задаваться различными способами. На границе рассматриваемой области можно задать: а) значение искомой функции; б) значения производных по пространственным координатам от искомой функции; в) уравнение баланса потоков. В этих случаях говорят о граничных условиях первого, второго и третьего рода соответственно.
В частности при моделировании процессов теплообмена распределение температуры в точках среды в различные моменты времени определяется из уравнения в частных производных (уравнения теплопроводности). Для однозначного определения температурного поля T(x, у, z, t) помимо уравнения теплопроводности необходимо сформулировать дополнительные (замыкающие) соотношения, так как решения уравнений в частных производных определяются с точностью до некоторых произвольных функций. Чтобы конкретизировать решение формулируются некоторые дополнительные соотношения (в некоторых точках известно само решение, или производные от решения в некоторых направлениях и т. д.) Например, пусть расчет температурного поля для уравнения теплопроводности осуществляется в некоторой выбранной области пространства. Для упрощения рассмотрим случай с постоянной расчетной областью Будем считать для определенности, что исследуется процесс теплопередачи, начиная с момента времени t = 0 до некоторого момента времени t = t max > 0. Поэтому решение уравнения теплопроводности (3) определяется в цилиндре Q={(x,y,z,t)|(x,y,z)
Это уравнение содержит частные производные, как по пространству, так и по времени. Поэтому дополнительные соотношения должны задаваться на множествах точек пространственной области Для уравнения теплопроводности обычно ставятся краевые задачи. В этом случае дополнительные соотношения задаются на границе Q и называются краевыми условиями. Условия на боковой поверхности цилиндра Q соответствуют условиям по пространственным переменным (на границе пространственной области Имеется возможность задания и более сложных условий. Например, вместо начальных условий при t = 0 могут быть заданы дополнительные условия на другом сечении цилиндра Q, например, при некотором t = t*. Другими словами, множество точек, где заданы дополнительные соотношения, может лежать и внутри Q. Обычно считается, что температурное поле задано на начальный момент времени, т.е.
При рассмотрении высокоинтенсивных температурных процессов, например на основе гиперболического уравнения теплопроводности, необходимо задавать два условия по времени:
где Например, в начальный момент времени известна температура и скорость ее изменения во времени. Это позволяет задать помимо (4) и условие (5):
Задание условий типа (4) требует при прикладном моделировании проведения прямых измерений температуры в некоторый фиксированный момент времени. Такие измерения не всегда возможны. Поэтому могут использоваться и другие подходы. Например, для уравнения (3) могут быть приемлемыми условия в конечный момент времени, т.е. вместо условия (4) задано условие (6):
В этом случае по условиям (6) необходимо на основе уравнения теплопроводности восстановить температурное поле в предыдущий момент времени t < t max. Таким образом, мы формулируем ретроспективную задачудля уравнения теплопроводности.
Среди граничных условий для уравнения теплопроводности (условия первого, второго и третьего рода) наиболее простая ситуация характеризуется заданием температурного поля на границе
где Г – боковая поверхность Граничные условия второго рода (условия Неймана) соответствуют заданию на границе теплового потока. Для уравнения теплопроводности (3) в изотропной среде (независимость свойств физических объектов от направления) оно записывается в виде
где через д/дп обозначена внешняя по отношению к области Более сложная ситуация возникает с постановкой граничных условий второго рода для уравнения теплопроводности в анизотропных средах [13]. Граничное условие третьего рода моделирует конвективный теплообмен между поверхностью твердого тела с окружающей средой, которая имеет температуру Т с. Обычно считается, что тепловой поток пропорционален разности температур между поверхностью и окружающей средой и поэтому для изотропной среды имеем
где Граничные условия третьего рода могут рассматриваться как наиболее общие из приведенных выше. Эти условия можно записать в форме
Тогда при
Таким образом, в общем виде ММ на микроуровне можно представить в следующем виде
(11)
где
|
||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.191.22 (0.023 с.) |
 векторной функции скорости
векторной функции скорости 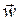 (x,y,z,t) элементарного объема учитывают 1) массовые (объемные) силы (силы тяжести
(x,y,z,t) элементарного объема учитывают 1) массовые (объемные) силы (силы тяжести 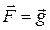 ), 2) поверхностные силы, к которым относятся силы давление P, а также силы трения за счет вязкости
), 2) поверхностные силы, к которым относятся силы давление P, а также силы трения за счет вязкости  и в декартовой системе координат имеют вид [5]:
и в декартовой системе координат имеют вид [5]: (1)
(1) ,
,  ,
,  – характеризуют изменение скорости во времени в какой-либо точке жидкости (локальное изменение скорости),
– характеризуют изменение скорости во времени в какой-либо точке жидкости (локальное изменение скорости), 

 скорости изменения координат во времени (проекции вектора скорости
скорости изменения координат во времени (проекции вектора скорости  – характеризуют изменения скорости при переходе от точки к точке; F x, F y, F z– проекции вектора силы
– характеризуют изменения скорости при переходе от точки к точке; F x, F y, F z– проекции вектора силы  на оси координат;
на оси координат;  – плотность; P – давление;
– плотность; P – давление; 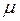 – коэффициент вязкости.
– коэффициент вязкости.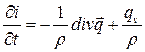 ,
, ;
;  – количество теплоты, выделяемое внутренними источниками в элементарном объеме в единицу времени (мощность внутренних источников).
– количество теплоты, выделяемое внутренними источниками в элементарном объеме в единицу времени (мощность внутренних источников). , а также с учетом
, а также с учетом  получим следующее выражение уравнения энергии
получим следующее выражение уравнения энергии , (2)
, (2) – коэффициент температуропроводности;
– коэффициент температуропроводности;  – характеризует изменение температуры во времени в какой-либо точке жидкости (локальное изменение температуры);
– характеризует изменение температуры во времени в какой-либо точке жидкости (локальное изменение температуры);  – характеризует изме-нение температуры при переходе от точки к точке (конвективное изменение температуры).
– характеризует изме-нение температуры при переходе от точки к точке (конвективное изменение температуры). , (конвективное изменение не учитывается), то уравнение энергии переходит в уравнение теплопроводности
, (конвективное изменение не учитывается), то уравнение энергии переходит в уравнение теплопроводности . (3)
. (3) , в которой и определяется решение уравнения теплопроводности [12, 13].
, в которой и определяется решение уравнения теплопроводности [12, 13]. Ω, 0<t<tmax}, т.е.
Ω, 0<t<tmax}, т.е. , (x,y,z,t)
, (x,y,z,t) 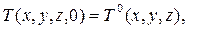 (x,y,z)
(x,y,z)  , (x,y,z,t)
, (x,y,z,t)  – определяет мощность внутренних источников теплоты.
– определяет мощность внутренних источников теплоты. (x,y,z)
(x,y,z)  ,(x,y,z)
,(x,y,z)  (граничные условия первого рода):
(граничные условия первого рода):
 , (7)
, (7)
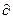 Ω, 0<t<tmax}.Условия первого рода (7) называются также условиями Дирихле.
Ω, 0<t<tmax}.Условия первого рода (7) называются также условиями Дирихле.
 ,
,  , (8)
, (8) .
.
 , (9)
, (9) – коэффициент теплоотдачи.
– коэффициент теплоотдачи. ,
,  à0 из (10) мы получим условие второго рода (8) и, напротив, при
à0 из (10) мы получим условие второго рода (8) и, напротив, при  следуют условия первого рода (7).
следуют условия первого рода (7).
 – дифференциальное уравнение
– дифференциальное уравнение – краевые условия,
– краевые условия, – коэффициенты;
– коэффициенты;  – дифференциальные операторы;
– дифференциальные операторы;  – заданная функция;
– заданная функция;  – зависимая (фазовая) переменная;
– зависимая (фазовая) переменная;  – вектор пространственных координат.
– вектор пространственных координат.


