Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод конечных элементов (МКЭ)
Основная идея МКЭ – аппроксимация самого решения дифференциального уравнения. Для одномерной стационарной задачи (пункт 2.2) получаем следующий алгоритм: 1) Замена исходной непрерывной области R дискретным аналогом – совокупностью конечных элементов (для одномерного случая отрезков) 2) Замена (аппроксимация) искомой непрерывной функции 3) Объединение конечных элементов (КЭ) в ансамбль с образованием системы алгебраических уравнений (по числу КЭ). 4) Определение узловых значений 5) Определение коэффициентов Таким образом, решение ДУ получают не в виде таблицы (МКР), а в виде набора непрерывных функций на множестве КЭ. Аппроксимирующие функции чаще всего выбирают из числа линейных, квадратичных или кубических полиномов. Для каждого элемента можно подбирать свой полином, но таким образом, чтобы сохранить непрерывность величины вдоль границ элемента. В сплошной среде число точек связи бесконечно. Понятие КЭ представляет собой попытку преодолеть эту трудность путем разбиения сплошного тела на отдельные элементы, которые взаимодействуют между собой только в узловых точках. Принципы конечно-элементного анализа нашли применение в ряде современных программ, таких как ANSYS, NASTRAN, FLUENT, STAR-CD [7, 16-18]. Исторически возникновение МКЭ связано с решением задач космических исследований [7]. Этот метод возник при решении задач строительной механики и теории упругости, а уже потом был осмыслен математиками, которые часто называют данный метод вариационно-разностным, подчеркивая тем самым его математическую природу. Проведение математического обоснования МКЭ (теоретический анализ его сходимости и точности результатов) позволило представителям инженерного направления решать сложные технические задачи не задумываясь над строгим обоснованием применяемых ими приемов, а построенные алгоритмы и программы проверять на известных точных решениях. Известны решения с помощью этого метода задач распространения тепла, задач гидромеханики и, в частности, задач о течении жидкости в пористой среде. Область применения МКЭ существенно расширилась, когда было показано, что уравнения, определяющие элементы в задачах строительной механики, распространения тепла, гидромеханики, могут быть легко получены с помощью таких вариантов метода взвешенных невязок, как метод Галёркина или способ наименьших квадратов. Установление этого факта сыграло важную роль в теоретическом обосновании МКЭ, т.к. позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, метод конечных элементов из численной процедуры решения задач строительной механики превратился в общий метод численного решения дифференциальных уравнений или систем дифференциальных уравнений. Этот прогресс был достигнут за довольно короткий срок благодаря совершенствованию ЭВМ.
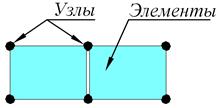
Основная идея метода конечных элементов состоит в том, что любую непрерывную величину (перемещение, температура, давление и т. п.) можно аппроксимировать моделью, состоящей из отдельных элементов (участков). На каждом из этих элементов исследуемая непрерывная величина аппроксимируется кусочно-непрерывной функцией, которая строится на значениях исследуемой непрерывной величины в конечном числе точек рассматриваемого элемента. В общем случае непрерывная величина заранее неизвестна, и нужно определить значения этой величины в некоторых внутренних точках области. Дискретную модель, однако, очень легко построить, если сначала предположить, что известны числовые значения этой величины в некоторых внутренних точках области (в дальнейшем эти точки назовем «узлами»). После этого можно перейти к общему случаю. Чаще всего при построении дискретной модели непрерывной величины поступают следующим образом: 1. Область определения непрерывной величины разбивается на конечное число подобластей, называемых элементами. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют форму области. 2. В рассматриваемой области фиксируется конечное число точек. Эти точки называются узловыми точками или просто узлами. 3. Значение непрерывной величины в каждой узловой точке первоначально считается известным, однако необходимо помнить, что эти значения в действительности еще предстоит определить путем наложения на них дополнительных ограничений в зависимости от физической сущности задачи.
4. Используя значения исследуемой непрерывной величины в узловых точках и ту или иную аппроксимирующую функцию, определяют значение исследуемой величины внутри области. Поясним сказанное выше на примере исследования распределения температуры в стержне. В общем случае распределение температуры неизвестно, и мы хотим определить значения этой величины в некоторых точках. Методика построения дискретной' модели остается точно такой же, как описано выше, но с добавлением одного дополнительного шага. Первоначально считают значения температуры в некоторых точках в пределах стержня известными. Определяют множество узлов и значения температуры в этих узлах, которые теперь являются переменными, т. к. они заранее неизвестны. Область (в нашем случае - длина стержня) разбивается на элементы, для каждого из которых определяется аппроксимирующая функция. Узловые значения температуры должны быть теперь «выбраны» таким образом, чтобы с учетом граничных условий (например, значений температуры на концах стержня) обеспечить наилучшее приближение к истинному распределению температуры вдоль стержня. Этот «выбор» осуществляется путем минимизации некоторой величины, связанной с физической сущностью задачи. Если рассматривается задача распространения тепла, то минимизируется функция, связанная с соответствующим дифференциальным уравнением. Процесс минимизации сводится к решению систем линейных алгебраических уравнений относительно узловых значений температуры (в прочностных задачах, где определяются поля перемещений, деформаций и напряжений минимизируется потенциальная энергия деформированного тела). Аппроксимирующие функции чаще всего выбирают в виде линейных, квадратичных или кубических полиномов. Для каждого элемента можно подбирать свой полином, но полиномы подбираются таким образом, чтобы сохранить непрерывность вдоль границ элемента. Этот полином, связанный «функцией элемента». С этой точки зрения конструкцию можно рассматривать как некоторую совокупность конструкционных элементов, соединенных в конечном числе узловых точек. Таким образом, при использовании МКЭ решение краевой задачи ищется в виде набора функций, определенных на некоторых подобластях (конечных элементах). Решение задачи с применением МКЭ состоит из следующих основных этапов: 1) идентификация задачи, присвоение ей имени, создание чертежа конструкции; 2) создание геометрической модели, пригодной для МКЭ; 3) разбиение модели на сетку конечных элементов; 4) приложение к модели граничных условий; 5) численное решение системы уравнений (автоматически выполняется программами, реализующими МКЭ) 6) анализ результатов. Этапы 1–4 относятся к предпроцессорной стадии, этап 5 к процессорной стадии, этап 6 к постпроцессорной стадии. Наиболее трудоемкими из шести этапов решения задачи с помощью МКЭ являются 3-й этап – создание конечно-элементной модели (так как автоматическое построение сетки элементов не гарантирует от появления ошибок) и 4-й этап – приложение нагрузок и граничных условий.
Шестой этап может быть существенно облегчен за счет использования мощных инструментов визуализации результатов. Достоверность расчетов зависит от многих факторов, в том числе и от количества КЭ и, следовательно, более детальной прорисовки объекта, более точного учета изменения свойств вдоль координат. Однако если фазовые переменные (температуры, давления) не меняются значительно в пределах модели, то количество КЭ несущественно влияет на точность вычислений. Построенная модель делится на этапе 3 при помощи КЭ (рис. 9а) на отдельные составляющие достаточно простой формы. Имеются несколько наиболее употребительных типов форм: брус (рис. 9б), стержень (рис. 9в), тонкая пластина (рис. 9г), двумерное или трехмерное поле (рис. 9д). При построении общей модели объекта могут быть использованы различные типы форм.
а) б)
в) г)
д)
Рис. 9. Характерные типы форм из КЭ
В свою очередь эти формы могут быть образованы из КЭ различного порядка: линейные КЭ (элементы первого порядка рис. 10а) или параболические (элементы второго порядка рис. 10б).
а) б)
Рис. 10. Линейные и параболические КЭ Линейные КЭ имеют прямые стороны и узлы только в углах. Поэтому минимальное число узлов для трехмерного элемента равно 4. Параболические КЭ могут иметь один или несколько промежуточных узлов вдоль каждой из сторон. Именно благодаря этому стороны элемента могут быть криволинейными (параболическими). При равном количестве КЭ параболические элементы дают большую точность вычислений, т.к. они более точно воспроизводят криволинейную геометрию модели и имеют более точные функции формы (аппроксимирующие функции). Однако расчет с применением КЭ высоких порядков требует больших компьютерных ресурсов и большего машинного времени. В программном комплексе ANSYS имеется два основных метода построения сетки: построение произвольной сетки и построение упорядоченной сетки. Произвольная сетка строится автоматически, при этом соседние элементы могут существенно отличаться по размерам (упорядоченная сетка строится путем деления геометрических элементов модели на некоторое заданное число частей). В автоматически построенных сетках с большим числом элементов число узлов преобладает над числом элементов. Отношение между узлами и элементами для плоских произвольных сеток примерно 2:1 и для произвольных трехмерных сеток с четырехгранными элементами 6:1.
Очевидно, что чем меньше линейный размер конечного элемента h, тем большее количество элементов в модели, при этом время вычислений существенно возрастает, а ошибки анализа уменьшаются. Однако ошибки уменьшаются не до нуля, т. к. с увеличением числа элементов накапливаются ошибки округления в ЭВМ. Практика расчетов позволяет дать следующие рекомендации: 1) линейные элементы требуют более частой сетки, чем квадратичные элементы (с одним промежуточным узлом) или кубичные (с двумя промежуточными узлами); 2) упорядоченная сетка (рис. 11б) является более предпочтительной, чем произвольная сетка (рис. 11а); 3) прямоугольная сетка с 4 узлами (рис. 11в)более предпочтительна, чем сетка с треугольными элементами (рис. 11б); 4) сетка треугольных элементов с промежуточными узлами (рис. 11г) имеет, по крайней мере, ту же самую точность, что и сетка прямоугольных элементов с 4-я узлами (рис. 11в);
а) б) в) г) д) е)
Рис. 11. Варианты организации сетки 5) прямоугольная сетка с 8 узлами (рис. 11д) является более предпочтительной, чем сетка треугольных элементов с промежуточными узлами (рис. 11г), несмотря на больший размер прямоугольных элементов; 6) аппроксимация внешнего воздействия кубическим полиномом (рис. 11е) не требует более мелкой сетки. Правильный выбор типов и размеров КЭ определяет точность расчетов. Например, более частая сетка требуется там, где ожидается наибольший градиент (концентратор наибольшего изменения) фазовой переменной (температура, давление) (рис. 12). В то же время более редкая сетка может применяться в зонах с более или менее постоянными фазовыми переменными, а также в областях, не представляющих для исследователя большого интереса.
Рис. 12. Применение частой и редкой сетки
Необходимо заметить, что точность результатов анализа уменьшается, если размеры соседних элементов вблизи концентратора существенно различны. Форма КЭ также влияет на точность вычислений. Следует избегать слишком узких и вытянутых элементов, т.к. элементы с примерно одинаковыми сторонами дают меньшую ошибку. Одновременно в сетке могут присутствовать треугольные и четырехугольные элементы, однако между ними не должно быть разрывов. Задание граничных условий - один из ответственных этапов конечно-элементного анализа. Граничные условия (например, перемещения или силы) прикладываются только к узлам. Максимальное число граничных условий, приложенных в узле, равно числу его степеней свободы – 3 (например, 3 силы или 3 перемещения). Необходимо обратить внимание, что число граничных условий должно быть минимально необходимым (не меньше и не больше). Так, например, не следует фиксировать все степени свободы (все перемещения) в каждом узле отдельного КЭ, не следует прикладывать силу в узле в том же самом направлении, в котором в данном узле зафиксировано смещение, полное отсутствие закрепления вдоль какой-нибудь оси может привести при анализе к кажущему сдвигу вдоль этой оси вследствие неизбежных ошибок округления при численных расчетах.
Точность результатов Численный анализ, к которому относится и МКЭ, требует некоторой идеализации реальной конструкции. Поэтому, несмотря на мощное развитие вычислительной техники, результаты вычислений по МКЭ не свободны от ошибок. Использование вычислительной техники в роли «черного ящика», без понимания основных процессов и этапов вычислений, может привести к существенным ошибкам. К сожалению, не исключены также и ошибки операторов. Приступая к конечно-элементному анализу, инженер должен понять: - к какой области анализа относится данная задача; - какая часть всей конструкции должна исследоваться подробнее; - какие упрощения можно допустить в данной задаче. Естественно, это требует определенной квалификации исследователя. Ошибки могут возникать на различных стадиях конечно-элементного анализа: при постановке задачи, дискретизации (построении модели), численном решении. Ошибки постановки задачи могут возникать, когда выбранный тип конечных элементов или их размер не соответствуют физическому поведению материала в конструкции. Несколько уменьшить эту ошибку (по крайней мере, ту ее часть, которая связана с размером конечного элемента) можно используя автоматическое построение сетки. Однако основным источником ошибок при постановке задачи является некорректное задание граничных условий. Таким образом, успех конечно-элементного анализа зависит от точности воспроизведения на модели граничных условий, геометрии и свойств материала конструкции. Ошибки дискретизации возникают при замене реальной конструкции ограниченным числом конечных элементов (с учетом их формы и размеров). Ошибки, связанные с численным решением систем уравнений, обычно менее значимы, чем перечисленные выше два типа ошибок. Существуют два метода конечно-элементного анализа: 1) h-метод (h – длина стороны конечного элемента); 2) р-метод (р – порядок полинома аппроксимирующей функции). Для повышения точности решения h-метод требует увеличения числа элементов. В соответствии с р-методом для увеличения точности необходимо повысить порядок полинома аппроксимирующей функции.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.184.237 (0.034 с.) |
 à
à 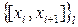 l =1,L
l =1,L кусочно-непрерывной на множестве конечных элементов, например для линейной аппроксимации
кусочно-непрерывной на множестве конечных элементов, например для линейной аппроксимации  à
à  , l =1,L.
, l =1,L. i=1,N одним из методом МКР.
i=1,N одним из методом МКР. для каждого КЭ.
для каждого КЭ.