
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем алгебраических уравнений
Решение систем линейных уравнений – одна из наиболее часто встречающихся задач в научных и инженерных расчетах. Многие приложения приводят к этой задаче непосредственно, кроме того системы линейных уравнений могут возникать как один из этапов в решении более сложных проблем. При этом обычно число уравнений равно числу неизвестных. Такую систему можно записать в матричном виде A x=b, где А – заданная квадратная матрица порядка n, b – заданный вектор-столбец с n компонентами и x – неизвестный вектор-столбец с n компонентами. В свернутом виде система может быть записана как
a21 x1+ a22 x2 +…+ a2n xn =b2, (78) …………………………………… an1 x1+ an2 x2 +…+ ann xn =bn .
Решением системы является вектор X*={x1*, x2*,…, xn*}, при подстановке которого в каждое уравнение системы получаем истинные равенства. Для решения СЛАУ применяют прямые (точные) и итерационные (приближенные) методы. Метод решения задачи относится к классу точных, если предполагается отсутствие округлений и с его помощью можно найти решение в результате конечного числа арифметических и логических операций. Среди прямых методов (используют конечное число преобразований системы) можно выделить методы Крамера, Гаусса, Гаусса–Жордана и др. В частности, метод Гаусса (гауссовых исключений) состоит в приведении исходной системы путем последовательных исключений неизвестных (при помощи элементарных операций над строками: перестановка строк; умножение строки на число отличное от нуля; сложение строк) к эквивалентной системе с треугольной (ступенчатой) матрицей (прямой ход метода Гаусса):
c22 x2 +…+ c2n xn =d2, ………………… xn =dn,
далее ее решают по рекуррентным формулам
xn =dn,
Итерационные методы реализуют стратегию постепенного приближения к решению X* путем построения соответствующей последовательности векторов X0, X1,…, Xk. Вектор X0 называется начальным приближением, а переход от текущего k -го приближения (вектор Xk) к k+1 -му приближению – итерацией. Данный переход реализуется при помощи функционального оператора Xk+1 = F(Xk), вид которого определяется заданной системой и конкретным методом. Для итерационных методов (метод простой итерации, метод Зейделя и др.) решение получают всегда приближенным, в то же время необходимо отметить ряд преимуществ, которыми обладают последние по сравнению с прямыми методами:
1) меньшие затраты времени при получении решения; 2) значительно меньшие погрешности округления; 3) самоисправление случайных ошибок на очередном шаге; 4) особенная эффективность при работе с разряженными матрицами (большое количество коэффициентов которых равно нулю), а также для систем большой размерности (103–106). Метод простой итерации реализует переход к k+1 -му приближению, используя при определении каждой координаты нового вектора координат только предыдущего k- го приближения Xk+1 = F(Xk). Пусть дана СЛАУ вида
a21 x1+ a22 x2 +…+ a2n xn + a2n+1 =0, (79) …………………………………… an1 x1+ an2 x2 +…+ ann xn + ann+1 =0.
Выразив из каждого уравнения соответствующую координату, получим
x2=с21 x1+ с22 x2 +…+ с2n xn + с2n+1, (80) …………………………………… xn=сn1 x1+ сn2 x2 +…+ сnn xn + сnn+1 . Для обеспечения условий сходимости (сходимость, или устойчивость, метода обеспечивается при любом начальном приближении X0, если норма матрицы, составленной из коэффициентов только при неизвестных в системе (2) меньше единицы, т.е., например,
где Если после данных преобразований сходимость не обеспечивается (единичные случаи), исходную систему необходимо преобразовать в эквивалентную. Это достигается путем попарного сложения или вычитания уравнений. Далее текущее приближение Xk подставляют в правую часть системы (2), тогда в левой части получают координаты нового уточненного приближения Xk+1. В качестве начального приближения X0 можно выбрать столбец свободных членов b или нулевой вектор. Окончанием итерационного процесса может служить выполнение условия
где e – заданная погрешность приближенного решения.
Метод Зейделя является модификацией метода простой итерации. В целях ускорения сходимости он реализует переход к k+1 -му приближению, используя при определении координат нового вектора не только предыдущее k- е приближение, но и вычисленные на данный момент координаты k+1- го приближения Xk+1 = F(Xk, Xk+1):
x2k+1=с21 x1k+1+ с22 x2k+…+ с2n xnk + с2n+1, (82) …………………………………… xnk+1=сn1 x1k+1+ сn2 x2k+1+…+ сnn xnk + сnn+1 .
Дальнейшее ускорение сходимости последовательности приближений достигается в методе последовательной верхней релаксации. Для специального вида матриц, например симметричных, положительно определенных, имеется также семейство методов сопряженных градиентов или сопряженных направлений [9]. В целом для обеспечения сходимости итерационного метода достаточно, чтобы выполнялось условие || A ||<1 или || С ||<1 по какой-либо норме матрицы, согласованной с нормой векторов. Если для векторов x =(x1,x2,…,xn) введена норма ||x||, то согласованной с ней нормой матриц называют величину
Таблица 2
Примечание: В общем случае система может включать m уравнений относительно n неизвестных
a21 x1+ a22 x2 +…+ a2n xn =b2, …………………………………… am1 x1+ am2 x2 +…+ am n xn =bm .
Тогда данная система совместна, если она имеет хотя бы одно решение, и несовместна, если не имеет ни одного.
Во многих случаях применение линейных моделей даже для приближенного описания реальных явлений уже недостаточно. Одной из наиболее известных классических нелинейных задач является нахождение нулей полинома. Среди источников систем нелинейных уравнений можно выделить задачи вычисления интегралов (квадратурные формулы Гаусса для вычисления площадей), задачи минимизации функции, задачи интерполяции данных в нелинейных моделях, усложненные модели популяций и т.д. [9]. При этом между линейными и нелинейными уравнениями можно выделить следующие фундаментальные отличия: 1. Любая невырожденная СЛАУ имеет единственное решение. Для нелинейных уравнений вещественных решений может не существовать вообще (как, например, для уравнения f(x)=sinx+2=0), или их может быть много, как в уравнении f(x)=sinx=0. 2. Любая СЛАУ может быть точно решена за фиксированное, конечное число арифметических операций (примерно n3/3 для метода исключений Гаусса). Только некоторые нелинейные уравнения специального вида могут быть решены точно за конечное число шагов (полиномы до 4-й степени). 3. Значительные трудности обеспечения гарантий существования решения или сходимости к нему для СНЛУ. Поэтому для большинства практических задач при решении нелинейных уравнений и их систем используют приближенные итерационные методы поиска некоторого вещественного решения. Нахождение всех решений нелинейных уравнений все еще остается предметом исследований (исключая полиномиальные уравнения).
В общем случае систему нелинейных уравнений можно представить в виде F(X)=0, или
f2 (x1, x2,…,xn)=0, (83) ……………………… fn (x1, x2,…,xn)=0.
Тогда решением системы будет вектор X*={x1*, x2*,…, xn*}, при подстановке которого в каждое уравнение системы получаем истинные равенства F(X*)=0. С учетом использования приближенных методов понятие «решение» расширяют. Говорят, что
Решение отдельного нелинейного уравнения f(x)=0 (f(x) – непрерывная функция на интервале [a,b]) с учетом возможности множества решений включает два этапа. На первом, который называется отделением корней, находятся интервалы [a,b] k, длина которых не больше единицы, а функция на концах имеет противоположные знаки. В качестве алгоритма можно использовать простой перебор значений аргумента с некоторым шагом h (xi+1=xi+h), вплоть до наступления моментов f(xi+1)×f(xi)<0. На втором для каждого выделенного k -го интервала уточняются значения корня одним из рассматриваемых далее методов. Метод половинного деления (бисекции, дихотомии, проб) на каждом шаге итерации (сужения) делит текущий интервал [a,b] пополам: с=(a+b)/2. Если выполняется условие |f(c)|<e, то c является искомым корнем. В противном случае выбирается та часть интервала ([a,c] или [c,b]), на границах которого функция имеет различные знаки. Далее процедура повторяется. Для устранения ситуаций «зацикливание», а также ускорения процесса нахождения корня желательно ограничить число приближений к корню 30 итерациями. Метод простой итерации (последовательных приближений) предполагает замену исходного уравнения вида f(x)=0 на равносильное ему уравнение x=g(x). Далее текущее k -е приближение xk подставляют в правую часть преобразованного уравнения, получая в левой части более точное k+1 -е xk+1=g(xk). Процесс начинается с произвольного выбора начального приближения x0 и заканчивается при выполнении условия | xk+1 – xk | <e или | f(xk) | <e. Контроль сходимости метода может быть осуществлен при помощи условия |g¢(xk)|=|(g(xk)–g(xk-1))/(xk – xk-1)|<1, если оно не выполняется, необходимо прекращать вычисления. Кроме того, могут быть использованы метод Ньютона (касательных), метод хорд (ложного положения, пропорциональных частей), их комбинация, а также метод секущих [9]. При решении систем нелинейных уравнений можно выделить метод простой итерации и метод Ньютона. Метод простой итерации является развитием аналогичного метода для одного уравнения (аналогичен методу простой итерации для решения СЛАУ) и основан на допущении о возможности преобразования системы (47) к виду (48)
x2=g2 (x1, x2,…,xn), (84) ……………………… xn=gn (x1, x2,…,xn).
Успех процесса приближения во многом определяется удачным выбором начального вектора Xk=1 (он должен быть достаточно близким к истинному решению). Метод гарантированно сходится, если выполняется условие || J(x1, x2,…,xn)||<1, где J(x1, x2,…,xn) – матрица Якоби для функций g1,…, gn, а || J || – ее норма. Тогда для системы из двух уравнений
а начальное приближение должно удовлетворять условиям
Метод Ньютона реализует идею предварительной линеаризации исходной СНЛУ, он обеспечивает значительно более быструю сходимость и является наиболее распространенным методом. В основе его лежит разложение функции в ряд Тейлора. Тогда для системы (47), состоящей из двух уравнений для двух неизвестных, получим
где R1 и R2 – члены ряда более высоких порядков. Если приращения Dx1 и Dx2 выбрать так, чтобы величины x1 + Dx1 и x2 + Dx2 были близки к корням, то левые части соответствующих уравнений системы (49) будут примерно равны нулю. Отбросив члены более высоких порядков, сведем задачу к решению системы линейных алгебраических уравнений
где решением является вектор DХ={Dx1, Dx2 }. Найденные значения Dx1, Dx2 используют в виде поправок к текущему приближению Xk+1 = Xk + DХk. Расчет прекращается при выполнении условия DХk<e.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 137; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.94.251 (0.037 с.) |
 , i=1,2,…,n. Тогда в развернутом виде
, i=1,2,…,n. Тогда в развернутом виде a11 x1+ a12 x2 +…+ a1n xn =b1,
a11 x1+ a12 x2 +…+ a1n xn =b1, x1+ с12 x2 +…+ с1n xn =d1,
x1+ с12 x2 +…+ с1n xn =d1, , i=n – 1,n – 2,…, 1.
, i=n – 1,n – 2,…, 1. a11 x1+ a12 x2 +…+ a1n xn + a1n+1 =0,
a11 x1+ a12 x2 +…+ a1n xn + a1n+1 =0, x1=с11 x1+ с12 x2 +…+ с1n xn + с1n+1,
x1=с11 x1+ с12 x2 +…+ с1n xn + с1n+1, при i= 1,2,…,n) при переходе от системы (1) к системе (2) можно воспользоваться следующими преобразованиями:
при i= 1,2,…,n) при переходе от системы (1) к системе (2) можно воспользоваться следующими преобразованиями: ,
,  , (81)
, (81) .
. ,
, x1k+1=с11 x1k+ с12 x2k+…+ с1n-1 xn-1k +с1n xnk+ с1n+1,
x1k+1=с11 x1k+ с12 x2k+…+ с1n-1 xn-1k +с1n xnk+ с1n+1, . Чаще всего используют нормы векторов и соответствующих согласованных норм матриц, представленные в табл. 2.
. Чаще всего используют нормы векторов и соответствующих согласованных норм матриц, представленные в табл. 2.
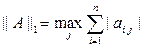



 или с учетом ||A||2£||A|| e
или с учетом ||A||2£||A|| e

 максимальное собственное значение матрицы
максимальное собственное значение матрицы 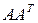 .
. a11 x1+ a12 x2 +…+ a1n xn =b1,
a11 x1+ a12 x2 +…+ a1n xn =b1, f1 (x1, x2,…,xn)=0,
f1 (x1, x2,…,xn)=0, приближенно удовлетворяет («решает») системе(у) F(X)=0, если
приближенно удовлетворяет («решает») системе(у) F(X)=0, если  , или
, или  .
.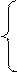 x1=g1 (x1, x2,…,xn),
x1=g1 (x1, x2,…,xn), ,
, и
и  .
.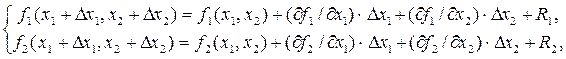 (85)
(85)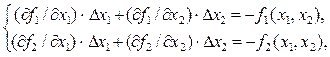 или
или 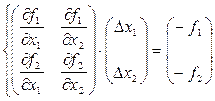 ,
,


