
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяция и аппроксимация данных⇐ ПредыдущаяСтр 12 из 12
Если информации о моделируемом объекте (процессе) недостаточно или он настолько сложен (имеет случайный характер), что невозможно составить его детерминированную модель, используют стохастические модели и соответствующие экспериментально-статистические методы. На практике весьма распространенной является задача определения функции (аналитической зависимости), которая должна соответствовать некоторым данным, полученным, например, при проведении экспериментальных исследований. При этом можно выделить два направления приближения функции – процесс интерполяции, определяющий вид функции, совпадающей с табличными данными, а также процесс аппроксимации, направленный на восстановление функциональной зависимости по данным эксперимента, возможно содержащего ошибки. Аппроксимация при этом должна обеспечивать оптимальное расположение линии (поверхности для многофакторного эксперимента) функции среди множества экспериментальных точек, не обязательно совпадающей с ними. Простейшим случаем интерполяции является определение вида функции f(x) одной переменной, проходящей через заданные точки (xi, yi), т.е. f(xi)=yi, i=1,…,N (рис.19а).
xx а) б) Рис. 19. Виды аппроксимации
Говорят, что функция f интерполирует данные, и в этом случае она называется интерполянтом, или интерполирующей функцией. Как видно из графика, в зависимости от способа интерполяции можно получить различные интерполянты. Отсюда следует: 1) данные (xi, yi) сами по себе не могут определить интерполянт, и для фиксированного набора данных существует бесконечное множество интерполянтов; 2) интерполяция может быть полезна только в том случае, если данные не содержат ошибок, если же, например, yi содержит погрешности, данные необходимо аппроксимировать как-то по-другому. Наиболее употребительным способом аппроксимации данных, содержащих ошибки, является метод наименьших квадратов. Он позволяет определить вид функции с минимальной суммой квадратов отклонений ее значений от экспериментальных. На рис. 19б отражен вариант такой функции при одномерной линейной аппроксимации. В общем случае задача аппроксимации данных решается для нелинейной функции многих переменных.
Так как в реальном процессе всегда существуют неуправляемые и неконтролируемые переменные, результат эксперимента есть случайная величина. Пусть, например, требуется исследовать зависимость y(x1, x2,…xm), причем величины y и Х={x1, x2,…xm} измеряются в одних и тех же экспериментах. Будем считать, что погрешность измерения величин xj пренебрежимо мала по сравнению с погрешностью измерения величины y, т.е. величины xj измеряются точно, в то время как измерение величины y содержит случайные погрешности. Таким образом, результаты эксперимента можно рассматривать как выборочные значения случайной величины h(X), зависящей от X, как от параметра. Регрессией называют зависимость
где b0 – свободный член уравнения регрессии; bj – линейные эффекты; bjj – квадратичные эффекты; bjk - эффекты взаимодействия. Коэффициенты уравнения (86) определяются методом наименьших квадратов из условия
где N – объем выборки. Необходимым условием минимума
Система (88) содержит столько же уравнений, сколько неизвестных коэффициентов Линейная регрессия одного параметра. Определим по методу наименьших квадратов коэффициенты линейного уравнения
Решая данную систему относительно
Коэффициент Для оценки силы линейной связи вычисляется выборочный коэффициент корреляции r*
Чем ближе r* к единице, тем выше линейность зависимости между x и y.
Параболическая регрессия одного параметра определяется коэффициентами параболического уравнения
Аналогично могут быть определены коэффициенты Трансцендентная регрессия одного параметра определяется коэффициентами уравнений показательного
Коэффициенты Для оценки силы (тесноты) нелинейной связи (проведения корреляционного анализа) вычисляется корреляционное отношение
где f1=N – 1, f2=N – l – числа степеней свободы; l – число связей, наложенных на выборку (для уравнения регрессии это число определяемых коэффициентов Чем больше q, тем сильнее связь (0£q£1). При q=0 однозначное отсутствие связи между случайными величинами возможно только для нормального распределения. В случае линейной регрессии (l=2) корреляционное отношение равно коэффициенту корреляции q=|r* |. Множественная регрессия предполагает определение коэффициентов (исследование корреляционной связи) для многофакторного уравнения. Например, для линейного случая уравнение множественной регрессии имеет вид Статистический анализ результатов (регрессионный анализ) проводится после определения уравнения регрессии и включает: оценку адекватности уравнения; проверку значимости всех коэффициентов При отсутствии параллельных опытов и, следовательно, дисперсии воспроизводимости, а также нормальном распределении случайных величин yi качество аппроксимации (адекватность) можно оценить по критерию Фишера
При одинаковом числе параллельных опытов (каждый i -й опыт с объемом выборки N ( Оценка значимости коэффициентов уравнения регрессии проводится по критерию Стьюдента
Определив для параметров
где b0, b1 – половина ширины доверительного интервала для для определения концов доверительных интервалов (доверительной полосы или коридора) выходной переменной
для определения доверительной области всей линии регрессии соответственно нижней (left) и верхней (right) границ полосы:
где Использование модели
7. Многовариантный анализ
Задачи оптимизации часто возникают в процессе поиска наилучшей конструкции какого-либо объекта. В общем случае оптимизация заключается в нахождении значения аргумента X*= { x1*,x2*,…,xn* }, при котором вещественная функция F(x1,x2,…,xn) на множестве S принимает минимальное или максимальное значение
Функция F представляет собой цель, а множество S выражает ограничения задачи. Если S есть все n -мерное пространство, говорят, что решается задача без ограничений (задача безусловной оптимизации). В противном случае рассматривается задача с ограничениями (условная оптимизация), определяющими множество S. Обычно это множество функций в виде условий равенств или неравенств. Вектор X, который удовлетворяет ограничениям, называется допустимым. Функция F(X) имеет глобальный (локальный) минимум в точке X*, если точка X* допустима и F(X*)£F(X) для всех допустимых точек X (которые «близки» к X*). Ограничимся в дальнейшем методами поиска приближенных локальных минимумов без ограничений (методы максимизации легко преобразуются в методы поиска минимума путем замены целевой функции на – F). Задачи условной оптимизации решать значительно труднее, особенно для нелинейных ограничений. Однако часто методы условной оптимизации являются развитием методов поиска экстремума без ограничений, включая их основные алгоритмы. Кроме того, возможно преобразование задач с ограничениями в задачи без ограничений, например для линейных функций. Одномерная оптимизация является в свою очередь частным случаем для выделенных задач, и заключается в поиске аргумента x* функции одной переменной F(x). При рассмотрении методов для упрощения будем считать функцию F(x) унимодальной на заданном отрезке [ a,b ], который называется интервалом неопределенности. Метод поразрядного приближения основан на замене исходного непрерывного отрезка [a,b] несколькими участками равной длины и последующего вычисления целевой функции в узлах образованной сетки. Как только очередное значение функции окажется хуже (больше) предыдущего F(xi+1)>F(xi), реализуется аналогичный поиск в обратном направлении с шагом сетки, например в 4 раза меньше прежнего. И так до тех пор, пока величина шага не станет меньше погрешности. Метод дихотомии реализует процедуру постепенного сужения исходного отрезка [ a,b ] вплоть до выполнения условия | b-a|<2e. При этом в целях экономии вычислительных ресурсов текущий интервал [a,b] делится при помощи двух дополнительных точек Метод золотого сечения обеспечивает использование на каждом шаге сужения отрезка (кроме первого) только одной дополнительной точки (необходимое для сравнения значение функции во второй точке берется из предыдущего шага). Для этого интервал неопределенности делится на две неравные части в соответствии с коэффициентом дробления k=0.618. В этом случае отношение длины большего участка к длине всего интервала равно отношению длины меньшего участка к длине большего (золотое сечение). Таким образом, на первом этапе значения функции определяются в двух дополнительных точках
Методы многомерной оптимизации используют для поиска экстремума функции многих переменных. Метод покоординатного спуска заключается в поочередном поиске минимума последовательно по координатам вектора X. Многомерная задача оптимизации сводится, таким образом, к последовательности одномерных задач на каждом шаге. После выбора исходного приближения X0ÎS вначале фиксируются значения всех координат кроме x1. Получаем функцию одной переменной f(x1), для которой одним из методов решается задача одномерной оптимизации. Затем переходим работе с координатой x2 и т.д. После исследования функции F(X) по всем координатам пространства проектирования проверяют условие | F(Xk+1) – F(Xk) |< e (где Xk – k -ое приближение вектора X), при выполнении которого расчет заканчивается. В противном случае проводят повторное исследование функции. Метод градиентного спуска использует информацию о градиенте функции F(X), который определяется выражением:
где После выбора начальной точки X0ÎS и определения в ней антиградиента делается шаг в выбранном направлении. Проверяется условие F(Xk+1)<F(Xk), при выполнении которого вычисляется антиградиент в новой точке с повторением процедуры. Если F(Xk+1)>F(Xk), то в направлении антиградиента делается шаг в два раза меньший и т.д. Перемещение в n -мерном пространстве на шаг h реализуется с помощью следующих выражений:
Процесс прекращается при выполнении условия
Метод наискорейшего спуска реализует движение в выбранном направлении не на один шаг, а на несколько – до тех пор, пока функция убывает. При этом спуск происходит более крупными шагами и, следовательно, антиградиент вычисляется в меньшем числе точек. Данный метод, таким образом, сводит многомерную задачу к последовательности одномерных задач аналогично методу покоординатного спуска. Псевдоградиентные методы обеспечивают выбор перспективного направления без вычисления градиента, использую лишь значения функции в нескольких точках. Примером может служить метод деформируемого многогранника (симплекс метод), для которого в пространстве проектирования вокруг исходного вектора X0ÎS строится многогранник с числом вершин (n+1). В качестве направления улучшения функции выбирается ось отражения наихудшей вершины относительно центра тяжести оставшихся вершин [11].
Библиографический список
1. Андерсон Д. Вычислительная гидромеханика и теплообмен: В 2 т.: Пер. с англ. /Д. Андерсон, Дж. Таннехилл, Р. Плетчер. М.: Мир, 1990. 728 с. 2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: Учеб. пособие / Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. М.: Наука, 1987. 600с. 3. Белова Д.А., Кузин Р.Е. Применение ЭВМ для анализа и синтеза автоматических систем управления / Д.А. Белова, Р.Е. Кузин М.: Энергия, 1979. 264 с. 4. Драйнер Н., Смит Г. Прикладной регрессионный анализ / Н. Драйнер, Г.Смит. М., 1973. 336 с. 5. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача: Учебник для вузов. 3-е изд., перераб. и доп. М.: Энергия, 1975. 488 с. 6. Норенков И.П. Основы автоматизированного проектирования: Учеб. для вузов. М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. 360 с. 7. Каплун А.Б., Морозов Е.М., Олферьева М.А. ANSYS в руках инженера: Практ. руководство. 2-е изд., испр. М.: Едиториал УРСС, 2004. 272 с. 8. Кафаров В.В. Методы кибернетики в химии и химической технологии. 4-е изд., перераб. и доп. М.: Химия, 1985. 448 с. 9. Каханер Д., Моулер К., Нэш С. Численные методы и математическое обеспечение: Пер. с англ. / Д. Каханер, К. Моулер, С. Нэш М.: Мир, 1998. 575 с. 10. Математическое моделирование теплообменных процессов компрессорных, холодильных, энергетических и технологических установок: Метод. указания по проведению лабораторных работ / Сост. И.А. Январев Омск: Изд-во ОмГТУ, 2006. 64 с. 11. Реклейтис Г. Оптимизация в технике: Пер. с англ. / Г. Реклейтис, А.Рейнвиндран, К. Рэгсдел. М.: Мир, 1986. 443 с. 12. Патанкар С.В. Численное решение задач теплопроводности и конвективного теплообмена при течениях в каналах / Пер. с англ. Е.В. Калабина; под ред. Г.Г. Янькова. М.: МЭИ, 2003. 312 с. 13. Самарский А.А., Вабищевич П.Н. Вычислительная теплопередача. М.: Едиториал УРСС, 2003. 784 c. 14. Статюха Г.А. Автоматизированное проектирование химико-технологических систем. К.: Выща шк. Головное изд-во, 1989. 400 с. 15. Турчак Л.И. Основы численных методов. М.: Наука, 1987. 320 с. 16. Шимкович Д.Г. Расчет конструкций в MSC/NASTRAN for Windows. – М.:ДМК Пресс, 2001. 448 с. 17. Январев И.А. Теплообменное оборудование и системы охлаждения компрессорных, холодильных и технологических установок. Учеб. пособие. / И.А. Январев. В.Л. Юша, В.П. Парфенов, В.А. Максименко, А.Д. Ваняшов. Омск: Изд-во ОмГТУ, 2005. 450 с. 18. Янишевская А.Г., Пергун И.Н. Использование программного комплекса ANSYS при расчетах тепловых процессов в машиностроении: Учеб. пособие. Омск: Изд-во ОмГТУ, 2001. 96 с.
СОДЕРЖАНИЕ
Редактор Т.А. Жирнова ИД № 06039 от 12.10.01 Сводный темплан 2006 г. Подписано в печать 25.07.06. Формат 60х84 1/16. Бумага офсетная. Отпечатано на дупликаторе. Усл. печ. л. 4,5. Уч.- изд. л. 4,5. Тираж Заказ.
Издательство ОмГТУ. 644050, Омск, пр. Мира, 11. Типография ОмГТУ.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.219.166 (0.089 с.) |

 y y
y y









 условного математического ожидания величины h(X) от переменной X, т.е.
условного математического ожидания величины h(X) от переменной X, т.е.  . Задача регрессионного анализа состоит в этом случае в восстановлении функциональной зависимости
. Задача регрессионного анализа состоит в этом случае в восстановлении функциональной зависимости  по результатам измерений (Xi, yi), i=1,2,…, N. Аппроксимируем неизвестную зависимость
по результатам измерений (Xi, yi), i=1,2,…, N. Аппроксимируем неизвестную зависимость  при помощи заданной функции уравнения регрессии
при помощи заданной функции уравнения регрессии  . Это значит, что результаты измерений можно представить в виде
. Это значит, что результаты измерений можно представить в виде  , где
, где  – неизвестные параметры регрессии, zi – случайные величины, характеризующие погрешности эксперимента. С учетом разложения исследуемой зависимости в ряд Тейлора в окрестности X0 и использования выборочных коэффициентов
– неизвестные параметры регрессии, zi – случайные величины, характеризующие погрешности эксперимента. С учетом разложения исследуемой зависимости в ряд Тейлора в окрестности X0 и использования выборочных коэффициентов  как оценок теоретических (b0=f(X0), b1=¶ f(X0)/¶ x1,…) уравнение регрессии можно записать в следующем общем виде [8]
как оценок теоретических (b0=f(X0), b1=¶ f(X0)/¶ x1,…) уравнение регрессии можно записать в следующем общем виде [8] , (86)
, (86) , (87)
, (87) является равенство нулю соответствующих частных производных
является равенство нулю соответствующих частных производных  ,
,  ,… Тогда после преобразования получим
,… Тогда после преобразования получим . (88)
. (88)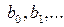 входит в уравнение регрессии и называется в математической статистике системой нормальных уравнений. Для решения системы (52) необходимо задать конкретный вид функции
входит в уравнение регрессии и называется в математической статистике системой нормальных уравнений. Для решения системы (52) необходимо задать конкретный вид функции  .
. . Тогда с учетом
. Тогда с учетом 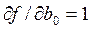 и
и  для системы (3) можно записать
для системы (3) можно записать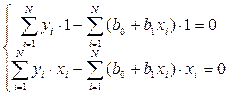 или
или  . (89)
. (89) и
и  , получим при помощи определителей следующие выражения:
, получим при помощи определителей следующие выражения: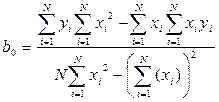 ,
,  .
. проще найти по известному
проще найти по известному 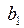 из первого уравнения системы (53)
из первого уравнения системы (53)  , где
, где  – средние значения x и y (
– средние значения x и y (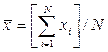 ).
). . (89)
. (89) . Тогда для параболы второго порядка
. Тогда для параболы второго порядка  система нормальных уравнений (88) имеет вид
система нормальных уравнений (88) имеет вид (90)
(90) , дробно-степенного типа
, дробно-степенного типа  и др. Обычно трансцендентную регрессию используют, чтобы уменьшить число неопределенных коэффициентов, т.к. при малых объемах выборки N увеличение порядка полинома может привести к росту остаточной дисперсии. Вычисление коэффициентов трансцендентной регрессии может оказаться весьма трудоемким вследствие необходимости решать систему нелинейных уравнений. Вычисления можно упростить, если провести замену переменных и линеаризовать приведенные выше зависимости путем логарифмирования:
и др. Обычно трансцендентную регрессию используют, чтобы уменьшить число неопределенных коэффициентов, т.к. при малых объемах выборки N увеличение порядка полинома может привести к росту остаточной дисперсии. Вычисление коэффициентов трансцендентной регрессии может оказаться весьма трудоемким вследствие необходимости решать систему нелинейных уравнений. Вычисления можно упростить, если провести замену переменных и линеаризовать приведенные выше зависимости путем логарифмирования:



 и
и 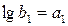
 и
и 


 или
или  определяются методом наименьших квадратов, значения которых используются для нахождения
определяются методом наименьших квадратов, значения которых используются для нахождения  .
. , (91)
, (91) );
);  – остаточная дисперсия;
– остаточная дисперсия;  - дисперсия относительно среднего.
- дисперсия относительно среднего. . Здесь, следовательно, требуется определить не линию регрессии, а поверхность (m =2) или гиперповерхность (m >2).
. Здесь, следовательно, требуется определить не линию регрессии, а поверхность (m =2) или гиперповерхность (m >2). и выходной переменной
и выходной переменной  .
. [4]. В данном случае он показывает, во сколько раз уменьшается рассеяние относительно полученного уравнения регрессии по сравнению с рассеянием относительно среднего. Чем больше значение F превышает табличное
[4]. В данном случае он показывает, во сколько раз уменьшается рассеяние относительно полученного уравнения регрессии по сравнению с рассеянием относительно среднего. Чем больше значение F превышает табличное  для выбранного уровня вероятности (значимости, надежности) p (обычно p =0.95) и чисел
для выбранного уровня вероятности (значимости, надежности) p (обычно p =0.95) и чисел  , тем эффективнее уравнение регрессии.
, тем эффективнее уравнение регрессии. ) проводится U раз
) проводится U раз  ) выборочные дисперсии
) выборочные дисперсии 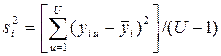 должны быть однородны. Последнее выполняется если справедливо условие Gmax<GpТАБ(N,U-1), где GpТАБ(N,U – 1) – табличное значение критерия Кохнера при уровне значимости p;
должны быть однородны. Последнее выполняется если справедливо условие Gmax<GpТАБ(N,U-1), где GpТАБ(N,U – 1) – табличное значение критерия Кохнера при уровне значимости p;  ;
;  – максимальное значение выборочной дисперсии. Для однородных выборочных дисперсий рассчитываются дисперсия воспроизводимости
– максимальное значение выборочной дисперсии. Для однородных выборочных дисперсий рассчитываются дисперсия воспроизводимости  и дисперсия адекватности
и дисперсия адекватности 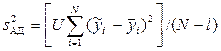 , которые необходимы для определения критерия Фишера
, которые необходимы для определения критерия Фишера  . Если расчетное значение меньше табличного
. Если расчетное значение меньше табличного 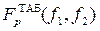 , то уравнение адекватно.
, то уравнение адекватно. , где
, где  – h -й коэффициент уравнения;
– h -й коэффициент уравнения;  – среднее квадратичное отклонение h -го коэффициента. Если
– среднее квадратичное отклонение h -го коэффициента. Если 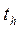 больше табличного
больше табличного  для выбранного уровня значимости p и степени свободы f=N(U –1 ), то коэффициент
для выбранного уровня значимости p и степени свободы f=N(U –1 ), то коэффициент  значимо отличается от нуля. Незначимые коэффициенты из уравнения исключаются с последующим пересчетом оставшихся. Чтобы не проводить повторных расчетов модели, при отбрасывании (включении) отдельных факторов применяют регрессионные уравнения в форме ортогональных полиномов (ортогональные многочлены Чебышева) [4, 8]. Для уравнения регрессии
значимо отличается от нуля. Незначимые коэффициенты из уравнения исключаются с последующим пересчетом оставшихся. Чтобы не проводить повторных расчетов модели, при отбрасывании (включении) отдельных факторов применяют регрессионные уравнения в форме ортогональных полиномов (ортогональные многочлены Чебышева) [4, 8]. Для уравнения регрессии 
 ,
,  .
. и табличные значения величины ta корня уравнения FN-2(
и табличные значения величины ta корня уравнения FN-2( ) =1–0.5a, функции распределения Стьюдента (t – распределение) с N-2 степенями свободы можно найти доверительные интервалы параметров модели
) =1–0.5a, функции распределения Стьюдента (t – распределение) с N-2 степенями свободы можно найти доверительные интервалы параметров модели  и доверительный коридор выходной переменной
и доверительный коридор выходной переменной  . Для уравнения регрессии
. Для уравнения регрессии  и
и  ,
, ,
, и
и  ;
; при каждом конкретном значении
при каждом конкретном значении  (доказано, что доверительный интервал накрывает истинное значение
(доказано, что доверительный интервал накрывает истинное значение  с вероятностью 1-a):
с вероятностью 1-a): ;
; ,
, – корень уравнения F2,N-2 (
– корень уравнения F2,N-2 (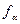 )=1–a; F2,N-2(x) – функция распределения Фишера (F – распределение) с 2 и N–2 степенями свободы.
)=1–a; F2,N-2(x) – функция распределения Фишера (F – распределение) с 2 и N–2 степенями свободы.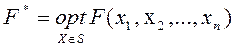 . (92)
. (92) и
и  на два участка [ a,x2 ] и [ x1,b ]. Далее в качестве нового текущего отрезка при помощи проверки условия F(x1)>F(x2) выбирается тот из них, который содержит искомый минимум (если условие выполняется, то новым текущим отрезком [ a,b ] будет участок [ x1,b ], в противном случае это [ a,x2 ]). По сравнению с методом поразрядного приближения более детальному исследованию подвергаются только перспективные участки, что существенно повышает экономичность модели.
на два участка [ a,x2 ] и [ x1,b ]. Далее в качестве нового текущего отрезка при помощи проверки условия F(x1)>F(x2) выбирается тот из них, который содержит искомый минимум (если условие выполняется, то новым текущим отрезком [ a,b ] будет участок [ x1,b ], в противном случае это [ a,x2 ]). По сравнению с методом поразрядного приближения более детальному исследованию подвергаются только перспективные участки, что существенно повышает экономичность модели.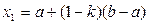 и
и  . После проверки условия F(x1)>F(x2) и выбора перспективного участка (по аналогии с методом дихотомии) на следующем шаге определяется только одна дополнительная точка. Если F(x1)>F(x2) выбираем участок [ x1,b ], т.е. a=x1. Одна дополнительная точка уже известна (x1=x2), и остается определить вторую для нового отрезка [ a,b ]
. После проверки условия F(x1)>F(x2) и выбора перспективного участка (по аналогии с методом дихотомии) на следующем шаге определяется только одна дополнительная точка. Если F(x1)>F(x2) выбираем участок [ x1,b ], т.е. a=x1. Одна дополнительная точка уже известна (x1=x2), и остается определить вторую для нового отрезка [ a,b ] 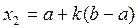 . Если F(x1)<F(x2) выбираем соответственно [ a,x2 ] т.е. b=x2, вторая дополнительная точка уже известна (x2=x1). Определяем первую
. Если F(x1)<F(x2) выбираем соответственно [ a,x2 ] т.е. b=x2, вторая дополнительная точка уже известна (x2=x1). Определяем первую  . Расчет заканчивается при выполнении условия | b-a|<e.
. Расчет заканчивается при выполнении условия | b-a|<e. , (93)
, (93)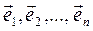 – единичные векторы (орты). Вектор-градиент перпендикулярен касательной к линии уровня функции (соответствующей текущему X) и указывает направление наискорейшего возрастания функции в этой точке. Тогда для организации градиентного спуска используют антиградиент (
– единичные векторы (орты). Вектор-градиент перпендикулярен касательной к линии уровня функции (соответствующей текущему X) и указывает направление наискорейшего возрастания функции в этой точке. Тогда для организации градиентного спуска используют антиградиент ( ).
).
 . (94)
. (94) < e. (95)
< e. (95)


