
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы теории массового обслуживания.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Предмет ТМО — системы массового обслуживания (СМО) и сети массового обслуживания. Под СМО понимают динамическую систему, предназначенную для эффективного обслуживания случайного потока заявок при ограниченных ресурсах системы. Поступающие на вход СМО однородные заявки в зависимости от порождающей причины делятся на типы, интенсивность потока заявок типа i (i=1…M) обозначено li. Совокупность заявок всех типов - входящий поток СМО. Обслуживание заявок выполняется m каналами. Различают универсальные и специализированные каналы обслуживания. Для универсального канала типа j считается известными функции распределения Fji(t) длительности обслуживания заявок произвольного типа. Для специализированных каналов функции распределения длительности обслуживания каналов заявок некоторых типов являются неопределёнными, назначение этих заявок на данный канал. В качестве процесса обслуживания могут быть представлены различные по своей физической природе процессы функционирования экономических, производственных, технических и других систем, например, потоки поставок продукции некоторому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха, заявки на обработку информации ЭВМ от удалённых терминалов и т.д. При этом характерным для работы таких объектов является случайное поведение заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени. Q - схемы можно исследовать аналитически и имитационными моделями. Последнее обеспечивает большую универсальность. Рассмотрим понятие массового обслуживания. В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание заявки. Это можно отобразить в виде некоторого i-ого прибора обслуживания Пi, состоящего из накопителя заявок Hi, в котором может находится одновременно li =0…LiH заявок, где LiH - ёмкость i-ого накопителя, и канала обслуживания заявок, Ki.
Рис. 3.2. Схема прибора СМО На каждый элемент прибора обслуживания Пi поступают потоки событий: в накопитель Hi поток заявок wi, на канал ki - поток обслуживания ui. Потоком событий (ПС) называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени. Различают потоки однородных и неоднородных событий. Однородный ПС характеризуется только моментами поступления этих событий (вызывающими моментами) и задаётся последовательностью {tn}={0£t1£t2…£tn£…}, где tn - момент поступления n- ого события - неотрицательное вещественное число. ОПС может быть также задан в виде последовательности промежутков времени между n-ым и n-1-ым событиями {tn}. Неоднородным ПС называется последовательность {tn, fn}, где tn- вызывающие моменты; fn- набор признаков события. Например, может быть задана принадлежность к тому или иному источнику заявок, наличие приоритета, возможность обслуживания тем или иным типом канала и т.п. ПС называется ординарным, если вероятность того, что на малый интервал времени Dt, примыкающий к моменту времени t попадает больше одного события Р³1(t, Dt) пренебрежительно мала. Стационарным ПС называется поток, для которого вероятность появления того или иного числа событий на интервале времени t зависит от длины этого участка и не зависит от того, где на оси времени 0 - t взят этот участок. Применительно к элементарному каналу обслуживания ki можно считать что поток заявок wiÎW, т.е. интервалы времени между моментами появления заявок на входе ki образуют подмножество неуправляемых переменных, а поток обслуживания uiÎU, т.е. интервалы времени между началом и окончанием обслуживания заявки образуют подмножество управляемых переменных. Заявки, обслуженные каналом ki и заявки, покинувшие прибор Пi по различным причинам не обслуженными, образуют выходной поток yiÎY. Процесс функционирования прибора обслуживания Пi можно представить как процесс изменения состояний его элементов во времени Zi(t). Переход в новое состояние для Пi означает изменение кол-ва заявок, которые в нём находятся (в канале ki и накопителе Hi). Т.о. вектор состояний для Пi имеет вид: Q-схемы реальных объектов образуются композицией многих элементарных приборов обслуживания Пi. Если ki различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема), а если приборы Пi и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание (многофазная Q-схема). Т.о. для задания Q-схемы необходимо оператор сопряжения R, отражающий взаимосвязь элементов структуры. Связи в Q-схеме изображают в виде стрелок (линий потока, отражающих направление движения заявок). Различают разомкнутые и замкнутые Q-схемы. В разомкнутой выходной поток не может снова поступить на какой-либо элемент, т.е. обратная связь отсутствует. Собственными (внутренними) параметрами Q-схемы будут являться кол-во фаз LФ, количество каналов в каждой фазе, Lkj, j=1… LФ, количество накопителей каждой фазы Lkj, k=1… LФ, ёмкость i-ого накопителя LiH. Следует отметить, что в теории массового обслуживания в зависимости от ёмкости накопителя применяют следующую терминологию: - системы с потерями (LiH=0, накопитель отсутствует); - системы с ожиданием (LiH®¥); - системы с ограниченной ёмкостью накопителя Нi (смешанные). Обозначим всю совокупность собственных параметров Q-схемы как подмножество Н. Для задания Q-схемы также необходимо описать алгоритмы её функционирования, которые определяют правила поведения заявок в различных неоднозначных ситуациях. В зависимости от места возникновения таких ситуаций различают алгоритмы (дисциплины) ожидания заявок в накопителе Нi и обслуживания заявок каналом ki. Неоднородность потока заявок учитывается с помощью введения класса приоритетов. В зависимости от динамики приоритетов Q-схемы различают статические и динамические приоритеты. Статические приоритеты назначаются заранее и не зависят от состояний Q-схемы, т.е. они являются фиксированными в пределах решения конкретной задачи моделирования. Динамические приоритеты возникают при моделировании. Исходя из правил выбора заявок из накопитель Нi на обслуживание каналом ki можно выделить относительные и абсолютные приоритеты. Относительный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель Н, ожидает окончания обслуживания представляющей заявки каналом ki и только после этого занимает канал. Абсолютный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель, прерывает обслуживание каналом ki заявки с более низким приоритетом и сами занимает канал (при этом вытесненная из ki заявка может либо покинуть систему, либо может быть снова записана на какое-то место в Нi). Необходимо также знать набор правил, по которым заявки покидают Нi и ki: для Нi – либо правила переполнения, либо правила ухода, связанные с истечением времени ожидания заявки в Нi; для ki – правила выбора маршрутов или направлений ухода. Кроме того, для заявок необходимо задать правила, по которым они остаются в канале ki, т.е. правила блокировок канала. При этом различают блокировки kiпо выходу и по входу. Такие блокировки отражают наличие управляющих связей в Q‑схеме, регулирующих поток заявок в зависимости от состояний Q‑схемы. Набор возможных алгоритмов поведения заявок в Q‑схеме можно представить в виде некоторого оператора алгоритмов поведения заявок А. Т.о. Q‑схема, описывающая процесс функционирования СМО любой сложности однозначно задаётся в виде набора множеств: Q = <W, U, H, Z, R, A>. W – множество входящих потоков; U – множество потоков обслуживания; Y – множество выходных потоков; Н – множество собственных параметров системы; Z – множество состояний системы; R – оператор сопряжения элементов в системе; А – оператор алгоритмов обслуживания заявок.
64. Основные понятия теории очередей. Классификация СМО. Теория массового обслуживания – область прикладной математики, занимающаяся анализом процессов в системах производства, обслуживания, управления, в которых однородные события повторяются многократно. Предметом теории массового обслуживания является установление связей между характером потока заявок, числа каналов обслуживания, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами. Системы массового обслуживания (СМО) — это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания. С позиции моделирования процесса массового обслуживания ситуации, когда образуются очереди заявок (требований) на обслуживание, возникают следующим образом. Поступив в обслуживающую систему, требование присоединяется к очереди других (ранее поступивших) требований. Канал обслуживания выбирает требование из находящихся в очереди, с тем, чтобы приступить к его обслуживанию. После завершения процедуры обслуживания очередного требования канал обслуживания приступает к обслуживанию следующего требования, если таковое имеется в блоке ожидания. Цикл функционирования системы массового обслуживания подобного рода повторяется многократно в течение всего периода работы обслуживающей системы. При этом предполагается, что переход системы на обслуживание очередного требования после завершения обслуживания предыдущего требования происходит мгновенно, в случайные моменты времени. Основными компонентами системы массового обслуживания любого вида являются: 1. входной поток поступающих требований или заявок на обслуживание; 2. дисциплина очереди; 3. механизм обслуживания. Независимо от характера процесса, протекающего в системе массового обслуживания, различают два основных вида СМО: 1. Системы с отказами. В таких системах заявка поступившая в момент, когда все каналы заняты, получает "отказ", покидает СМО и в дальнейшем процессе обслуживания не участвует. 2. Системы с ожиданием (с очередью). В таких системах заявка, поступившая в момент, когда все каналы заняты, становиться в очередь и ожидает, пока не освободиться один из каналов. Как только освободиться канал, принимается к обслуживанию одна из заявок, стоящих в очереди. Обслуживание в системе с ожиданием может быть "упорядоченным" (заявки обслуживаются в порядке поступления) и "неупорядоченным" (заявки обслуживаются в случайном порядке). Кроме того, в некоторых СМО применяется так называемое "обслуживание с приоритетом", когда некоторые заявки обслуживаются в первую очередь, предпочтительно перед другими. Системы с очередью оделяться на системы с неограниченным ожиданием и системы с ограниченным ожиданием. В системах с неограниченным ожиданием каждая заявка, поступавшая в момент, когда нет свободных каналов, становиться в очередь и "терпеливо" ждет освобождения канала, который примет ее к обслуживанию. Любая заявка, поступившая в СМО, рано или поздно будет обслужена. В системах с ограниченным ожиданием на пребывание заявки в очереди накладываются те или другие ограничения. Эти ограничения могут касаться длины очереди (числа заявок, одновременно находящихся в очереди), времени пребывания заявки в очереди(после какого-то срока пребывания в очереди заявка покидает очередь и уходит), общего времени пребывания заявки в СМО и т.д. СМО классифицируется по числу каналов обслуживания: · Одноканальные системы · Многоканальные системы СМО бывают открытые и замкнутые. В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии сама СМО(сколько каналов занято), в замкнутой - зависят. СМО различают по дисциплине очереди: с дисциплиной очереди FIFO, LIFO,случайный отбор заявок, с приоритетом. Приоритет может быть абсолютным – заявка с более высоким приоритетом вытесняет из под обслуживания заявку с более низким приоритетом. Приоритет может быть относительным - начатое обслуживание доводится до конца, а заявка с более высоким приоритетом имеет лишь право на лучшее место в очереди. В зависимости от типа СМО, при оценке ее эффективности могут применятся те или другие величины (показатели эффективности). Например, для СМО с отказами одной из важнейших характеристик ее продуктивности является так называемая абсолютная пропускная способность - среднее число заявок, которое может обслужить система за единицу времени. Наряду с абсолютной, часто рассматривается относительная пропускная способность СМО - средняя доля поступивших заявок, обслуживаемая системой (отношение среднего числа заявок, обслуживаемых системой в единицу времени, к среднему числу поступающих за это время заявок) Помимо абсолютной и относительной пропускной способностей, при анализе СМО с отказами нас могут, в зависимости от задачи исследования, интересовать и другие характеристики, например: · среднее число занятых каналов, · среднее относительное время простоя системы в целом и отдельного канала и т.д. 65. Задание процесса функционирования СМО. Основные характеристики функционирования СМО. Рассмотрим стационарный поток однородных заявок без последействия. Пусть Pk(t) вероятность появления k заявок в интервале времени t. Эта вероятность зависит только от и не зависит от начала отсчета времени, от поступления заявок в предыдущих временных интервалах. Пусть к тому же поток является ординарным, т. е. Pk(dt) при k >1 бесконечно мала в сравнении с малым интервалом dt. Если обозначить через число заявок в единицу времени (интенсивность потока), то можно показать, что для такого простейшего потока
Формула (1) определяет распределение Пуассона. Для пуассоновского потока можно обнаружить, что промежутки времени T между поступлениями заявок распределены по экспоненциальному (показательному) закону
(вероятность, что промежуток времени не превышает t). Естественно, что входной поток может описываться не только пуассоновским, но и другими распределениями (Эрланга, гиперэкспоненциальным и т.п.). Аналогичная ситуация имеет место и для выходного потока. Чаще всего используется показательный закон распределения времени обслуживания:
где m =1/tобс - интенсивность обслуживания (среднее число обслуживаний в единицу времени), tобс - среднее время обслуживания одной заявки. Пусть S - множество состояний системы и P(l, t+t / i, t) - вероятность того, что система, находившаяся в момент t в состоянии i, в момент t+t окажется в состоянии l. Для марковской системы (она привлекает нас отсутствием последействия) можно записать уравнения Чепмена-Колмогорова:
Если под состояниями понимать число заявок, то эти уравнения можно записать в виде:
Рассмотрим случай разомкнутой системы с простейшим входным потоком интенсивности l и одним каналом обслуживания с интенсивностью m. Возьмем интервал времени [t, t+dt]. В силу разомкнутости системы множество состояний системы S = { S0, S1, S2,..., Sk, Sk+1,... }, где Sk - состояние, когда в системе находится k заявок Попробуем оценить вероятности перехода между состояниями с учетом, того, что вероятность появления заявки в этом интервале времени равна l dt и вероятность завершения обслуживания предшествующей заявки равна m dt. Очевидно, что вероятность перехода S0>S1 равна l dt и вероятность перехода S1>S0 равна 1 - l dt. Если в системе присутствовали k>0 заявок (состояние Sk), то для перехода в состояние Sk-1 необходимо, чтобы заявка была обслужена и не поступило новой заявки; отсюда вероятность перехода Sk>Sk-1 равна m dt (1 - l dt) @ m dt. Для перехода из состояния Sk в состояние Sk+1 необходимо, чтобы поступила новая заявка, но ни одна из ранее поступивших не была обслужена: вероятность перехода SkЮSk+1 равна l dt(1-mdt) @ l dt. Вероятность для системы остаться в том же состоянии составит 1 - (l+m)dt. Тогда из (5) имеем
При dtЮ0 получаем дифференциальные уравнения состояний СМО:
Решение (6) при заданных начальных условиях достаточно сложно (здесь можно использовать преобразование Лапласа или численное решение задачи Коши для системы обыкновенных дифференциальных уравнений большого порядка, но едва ли это посильно непрофессионалу). Ограничимся рассмотрением установившегося режима, признаком которого является существование предела
В этом случае (6) приведется к бесконечной системе линейных алгебраических уравнений с трехдиагональной матрицей коэффициентов lP0 = mP1
Обозначив
имеем P1=rP0, P2=r2P0, P3=r3P0, P4=r4P0,..., Pk=rkP0,..., откуда с учетом P0 + P1 + P2 + P3 +... + Pk+... = 1 получаем при r < 1
Тогда
и
Обратите внимание на требование r < 1. Если это требование нарушено, то ни о каком установившемся режиме не может быть речи: очередь растет неограниченно (средняя продолжительность обслуживания больше среднего интервала времени между заявками). Теперь обратимся к аналогичной замкнутой системе с числом заявок, не превышающим n. Здесь система уравнений (6) приведется к конечной системе
которая для установившегося режима дает конечную систему линейных алгебраических уравнений
Решение этой системы
дает
и
Полученные выше решения можно обобщить на случай многоканальных систем c ограниченным ожиданием. Так, если СМО имеет N однотипных каналов обслуживания (интенсивность обслуживания равна Nm), m мест в очереди и к тому же число n возможных заявок превышает N+m (в противном случае нет проблем), то возникает система
из которой получаем для установившегося режима
Решение этой системы дает
Умение найти значения Pk дает возможность отыскать и ряд основных характеристик СМО. Основные характеристики СМО Значение P0 определяет вероятность того, что все каналы обслуживания свободны (находятся в состоянии простоя). Значение Pk определяет вероятность того, что в системе (в очереди и на обслуживании) находятся k заявок. Если k не превышает числа каналов N, то все заявки находятся на обслуживании и очередь отсутствует; в противном случае все каналы заняты и k-N заявок находится в очереди. Вероятность Pотк отказа в обслуживании определяется ситуацией занятости всех N каналов и всех m мест в очереди и равна PN+m. Среднее число занятых каналов Nзан определяется математическим ожиданием дискретной случайной величины [30]:
(мы опускаем здесь достаточно простые преобразования). Среднее число свободных каналов
Коэффициент простоя каналов
Коэффициент занятости каналов
Относительная пропускная способность (доля обслуженных заявок в общем числе поступавших в систему) определяется величиной
Абсолютная пропускная способность (среднее число заявок, обслуживаемых в единицу времени) определяется величиной
Средняя длина очереди [30]
Cреднее число заявок, находящихся в системе, складывается из средних значений занятости каналов и длины очереди
Среднее время пребывания заявки в очереди равно
Общее время пребывания заявки в очереди будет складываться из Tочер и среднего времени обслуживания
Полученные характеристики дают возможность анализа замкнутых и разомкнутых систем с отказами (m=0), с очередью или с ожиданием (m®Ґ) при простейшем входном потоке и однотипных параллельных каналах обслуживания с показательным законом длительности обслуживания (в частности, с фиксированной длительностью).
66. Стационарный режим функционирования СМО. Уравнения Колмогорова При длительном (теоретически бесконечном) функционировании системы она входит в состояние, при котором ее характеристики непосредственно от текущего времени не зависят, а изменяются исходя их внутренних взаимосвязей между ними. Такой режим функционирования называется стационарным. Он представляет наибольший интерес на практике, т. к. большинство реальных систем достаточно быстро оказываются в почти стационарном режиме. Не всякая система имеет стационарный режим. Неустановившийся (переходный) режим имеет место тогда, когда поведение системы продолжает оставаться функцией времени. Для того чтобы система имела стационарный режим, необходимо и достаточно, чтобы объем поступающей работы был меньше пропускной способности системы. Пусть l - интенсивность поступления заявок, m - интенсивность обслуживания заявок. Тогда для наличия стационарного режима необходимо и достаточно, чтобы l<m. Пусть r= Замечание: Если в системе либо обслуживание, либо поступление имеют случайный характер (не детерминированы), то при r=1 система также не имеет стационарного режима, при этом очередь и время ожидания будут бесконечно расти. Это объясняется тем, что ввиду случайности, систематически будут возникать сколь угодно большие случайные отклонения, вызывающие переполнение системы. В дальнейшем будем предполагать, что входящий поток требований является простейшим с экспоненциальным распределением интервалов времени поступления для соседних требований. Предположение о показательном распределении длительного обслуживания существенно упрощает исследование модели, поскольку процесс обслуживания обладает свойством отсутствия памяти. Процесс функционирования СМО можно представить через все ее возможные состояния, а также через интенсивность перехода из одного состояния в другое, т. е. процесс функционирования СМО – процесс с дискретными состояниями и непрерывным временем. Все возможные состояния можно заранее перенумеровать, переход системы из состояния в состояние осуществляется мгновенно, моменты перехода системы из состояния в состояние случайны. При анализе случайных процессов с дискретными состояниями удобно пользоваться графом состояний. S0, S1, … Sn – состояния. Переход из одного состояния в другое отмечается стрелкой.
Пример: S – техническое устройство, состоит из 2-х узлов, каждый из которых в случайный момент времени может выйти из строя, после чего мгновенно начинается ремонт узла, тоже продолжающийся случайное время. Возможные состояния: S0 – оба узла исправны S1 – первый ремонтируется, второй исправен S2 – второй ремонтируется, первый исправен S3 – оба ремонтируются. Т. к. поступающий поток ординарный, существуют переходы только между соседними состояниями.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 884; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.63.252 (0.01 с.) |


 , где
, где  - состояния накопителя, (
- состояния накопителя, ( - накопитель занят полностью;
- накопитель занят полностью;  - состояние канала ki (
- состояние канала ki (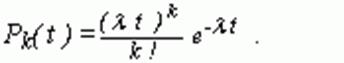 (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5)
 (6)
(6) (7)
(7) (8)
(8)
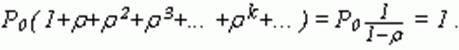





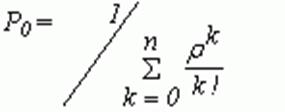








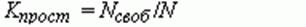
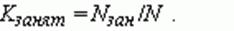





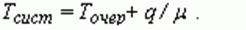
 - загрузка системы: среднее число заявок, приходящее за среднее время обслуживания одной заявки. Условие стационарности: r<1.
- загрузка системы: среднее число заявок, приходящее за среднее время обслуживания одной заявки. Условие стационарности: r<1.



