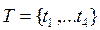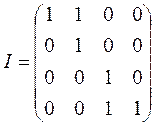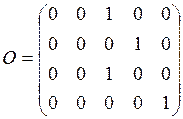Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсионный анализ результатов моделирования.Стр 1 из 5Следующая ⇒
При обработке и анализе результатов моделирования часто возникает задача сравнения средних выборок. Если в результате такой проверки окажется, что математическое ожидание совокупностей случайных переменных {у{1)}, {у{2)}, …, {у{n)} отличается незначительно, то статистический материал, полученный в результате моделирования, можно считать однородным (в случае равенства двух первых моментов). Это дает возможность объединить все совокупности в одну и позволяет существенно увеличить информацию о свойствах исследуемой модели Мм, а следовательно, и системы S. Попарное использование для этих целей критериев Смирнова и Стьюдента для проверки нулевой гипотезы затруднено в связи с наличием большого числа выборок при моделировании системы. Поэтому для этой цели используется дисперсионный анализ. дисперсионный анализ позволяет вместо проверки нулевой гипотезы о равенстве средних значений выборок проводить при обработке результатов моделирования проверку нулевой гипотезы о тождественности выборочной и генеральной дисперсий. Возможны и другие подходы к анализу и интерпретации результатов моделирования, но при этом необходимо помнить, что их эффективность существенно зависит от вида и свойств конкретной моделируемой системы S.
58. Математические схемы в моделировании систем. Формализация процесса функционирования систем.
Исходной информацией при построении математических моделей процессов функционирования систем служат данные о назначении и условиях работы исследуемой (проектируемой) системы S. Эта информация определяет основную цель моделирования системы S и позволяет сформулировать требования к разрабатываемой математической модели М. Введение понятия «математическая схема» позволяет рассматривать математику не как метод расчета, а как метод мышления, как средство формулирования понятий, что является наиболее важным при переходе от словесного описания системы к формальному представлению процесса ее функционирования в виде некоторой математической модели (аналитической или имитационной). При пользовании математической схемой исследователя системы S в первую очередь должен интересовать вопрос об адекватности отображения в виде конкретных схем реальных процессов в исследуемой системе, а не возможность получения ответа (результата решения) на конкретный вопрос исследования.
Математическую схему можно определить как звено при переходе от содержательного к формальному описанию процесса функционирования системы с учетом воздействия внешней среды, т. е. имеет место цепочка «описательная модель → математическая схема → математическая (аналитическая или (и) имитационная) модель». Общая схема процесса функционирования системы основана на следующих положениях: 1. любая система функционирует во времени, взаимодействует с внешней средой и в каждый момент времени может находиться в одном из возможных состояний. 2. на вход системы поступают входные сигналы 3. система способна выдавать выходные сигналы 4. состояние системы в момент времени определяется предыдущим состоянием и выходными сигналами. Модель объекта моделирования, т. е. системы S, можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества: · совокупность входных воздействий на систему · совокупность воздействий внешней среды · совокупность внутренних(собственных) параметров системы · совокупность выходных характеристик системы При этом в перечисленных подмножествах можно выделить управляемые и неуправляемые переменные. В общем случае Закон функционирования в общем случае может быть задан в виде функции, функционала, логических условий, словесного правила соответствия, в алгоритмической и табличной форме. Математическое описание системы моделирования во времени t называется динамическим. Для статических моделей процесс функционирования записывается уравнением
Типовые математические схемы В практике моделирования объектов в области системотехники и системного анализа на первоначальных этапах исследования системы рациональнее использовать типовые математические схемы: дифференциальные уравнения, конечные и вероятностные автоматы, системы массового обслуживания, сети Петри, агрегативные системы и т.д.
Типовые математические схемы имеют преимущества простоты и наглядности. В качестве детерминированных моделей, когда при исследовании случайные факторы не учитываются, для представления систем, функционирующих в непрерывном времени, используются дифференциальные, интегральные, интегродифференциальные и другие уравнения, а для представления систем, функционирующих в дискретном времени, конечные автоматы и конечно-разностные схемы. В качестве стохастических моделей (при учете случайных факторов) для представления систем с дискретным временем используются вероятностные автоматы, а для представления систем с непрерывным временем – системы массового обслуживания. Для анализа причинно-следственных связей в сложных системах, где одновременно параллельно протекает несколько процессов, применяют сети Петри. Для описания поведения непрерывных и дискретных, детерминированных и стохастических систем (например АСОИУ) можно применять обобщенный (универсальный) подход на основе агрегативной системы. При агрегативном описании сложный объект (система) расчленяется на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие взаимодействие частей. Таким образом, при построении математических моделей процессов функционирования систем можно выделить следующие основные подходы: · непрерывно-детерминированный (D-схемы); · дискретно-детерминированный (F-схемы); · дискретно-стохастический (Р-схемы); · непрерывно-стохастический (Q-схемы); · сетевой (N-схемы); · обобщенный или универсальный (А-схемы). 59. Математические схемы в моделировании систем. D-схемы Исходной информацией при построении математических моделей процессов функционирования систем служат данные о назначении и условиях работы исследуемой (проектируемой) системы S. Эта информация определяет основную цель моделирования системы S и позволяет сформулировать требования к разрабатываемой математической модели М. Введение понятия «математическая схема» позволяет рассматривать математику не как метод расчета, а как метод мышления, как средство формулирования понятий, что является наиболее важным при переходе от словесного описания системы к формальному представлению процесса ее функционирования в виде некоторой математической модели (аналитической или имитационной). При пользовании математической схемой исследователя системы S в первую очередь должен интересовать вопрос об адекватности отображения в виде конкретных схем реальных процессов в исследуемой системе, а не возможность получения ответа (результата решения) на конкретный вопрос исследования. Математическую схему можно определить как звено при переходе от содержательного к формальному описанию процесса функционирования системы с учетом воздействия внешней среды, т. е. имеет место цепочка «описательная модель → математическая схема → математическая (аналитическая или (и) имитационная) модель». При построении математических моделей процессов функционирования систем можно выделить следующие основные подходы:
· непрерывно-детерминированный (D-схемы); · дискретно-детерминированный (F-схемы); · дискретно-стохастический (Р-схемы); · непрерывно-стохастический (Q-схемы); · сетевой (N-схемы); · обобщенный или универсальный (А-схемы). особенностью непрерывно-детерминированного подхода является применение в качестве математических моделей дифференциальные уравнений. Дифференциальными уравнениями называются такие уравнения, в которых неизвестными являются функции одной или нескольких переменных, причем в уравнение входят не только функции, но и их производные различных порядков. Если неизвестные — функции многих переменных, то уравнения называются уравнениями в частных производных, в противном случае при рассмотрении функции только одной независимой переменной уравнения называются обыкновенными дифференциальными уравнениями. Обычно в таких математических моделях в качестве независимой переменной, от которой зависят неизвестные искомые функции, служит время t. Тогда математическое соотношение для детерминированных систем в общем виде будет
где Так как математические схемы такого вида отражают динамику изучаемой системы, т. е. ее поведение во времени, то они называются D-схемами (англ. dynamic). В простейшем случае обыкновенное дифференциальное уравнение имеет вид
Наиболее важно для системотехники приложение D-схем в качестве математического аппарата в теории автоматического управления. При решении задач системотехники важное значение имеют проблемы управления большими системами. Следует обратить внимание на системы автоматического управления — частный случай динамических систем, описываемых D-схемами и выделенных в отдельный класс моделей в силу их практической специфики. Описывая процессы автоматического управления, придерживаются обычно представления реального объекта в виде двух систем: управляющей и управляемой (объекта управления). Структура многомерной системы автоматического управления общего вида представлена на (рис. 3), где обозначены эндогенные переменные:
Современная управляющая система — это совокупность программно-технических средств, обеспечивающих достижение объектом управления определенной цели. Насколько точно объект управления достигает заданной цели, можно судить для одномерной системы по координате состояния y(t). Разность между заданным yзад(t) и действительным y(t) законами изменения управляемой величины есть ошибка управления h'(t)= yзад(t) - y(t). Системы, для которых ошибки управления h'(t) = 0 во все моменты времени, называются идеальными. На практике реализация идеальных систем невозможна. Таким образом, ошибка h'(t) — необходимый субстрат автоматического управления, основанного на принципе отрицательной обратной связи, так как для приведения в соответствие выходной переменной у(t) ее заданному значению используется информация об отклонении между ними. Задачей системы автоматического управления является изменение переменной у(t) согласно заданному закону с определенной точностью (с допустимой ошибкой). При проектировании и эксплуатации систем автоматического управления необходимо выбрать такие параметры системы S, которые обеспечили бы требуемую точность управления, а также устойчивость системы в переходном процессе. Если система устойчива, то представляют практический интерес поведение системы во времени, максимальное отклонение регулируемой переменной у(t) в переходном процессе, время переходного процесса и т. п. Выводы о свойствах систем автоматического управления различных классов можно сделать по виду дифференциальных уравнений, приближенно описывающих процессы в системах. Порядок дифференциального уравнения и значения его коэффициентов полностью определяются статическими и динамическими параметрами системы S. Таким образом, использование D-схем позволяет формализовать процесс функционирования непрерывно-детерминированных систем S и оценить их основные характеристики, применяя аналитический или имитационный подход, реализованный в виде соответствующего языка для моделирования непрерывных систем или использующий аналоговые и гибридные средства вычислительной техники.
60. Математические схемы в моделировании систем. (F-СХЕМЫ) Исходной информацией при построении математических моделей процессов функционирования систем служат данные о назначении и условиях работы исследуемой (проектируемой) системы S. Эта информация определяет основную цель моделирования системы S и позволяет сформулировать требования к разрабатываемой математической модели М. Введение понятия «математическая схема» позволяет рассматривать математику не как метод расчета, а как метод мышления, как средство формулирования понятий, что является наиболее важным при переходе от словесного описания системы к формальному представлению процесса ее функционирования в виде некоторой математической модели (аналитической или имитационной). При пользовании математической схемой исследователя системы S в первую очередь должен интересовать вопрос об адекватности отображения в виде конкретных схем реальных процессов в исследуемой системе, а не возможность получения ответа (результата решения) на конкретный вопрос исследования.
Математическую схему можно определить как звено при переходе от содержательного к формальному описанию процесса функционирования системы с учетом воздействия внешней среды, т. е. имеет место цепочка «описательная модель → математическая схема → математическая (аналитическая или (и) имитационная) модель». При построении математических моделей процессов функционирования систем можно выделить следующие основные подходы: · непрерывно-детерминированный (D-схемы); · дискретно-детерминированный (F-схемы); · дискретно-стохастический (Р-схемы); · непрерывно-стохастический (Q-схемы); · сетевой (N-схемы); · обобщенный или универсальный (А-схемы). дискретно-детерминированный подход характерен тем, что в качестве математического аппарата на этапе формализации процесса функционирования систем используется математического аппарата математический аппарат теории автоматов. Теория автоматов — это раздел теоретической кибернетики, в котором изучаются математические модели — автоматы. На основе этой теории система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени. Автомат можно представить как некоторое устройство (черный ящик), на которое подаются входные сигналы и снимаются выходные и которое может иметь некоторые внутренние состояния. Конечным автоматом называется автомат, у которого множество внутренних состояний и входных сигналов (а следовательно, и множество выходных сигналов) являются конечными множествами. Абстрактно конечный автомат (англ. finite automata) можно представить как математическую схему (F-схему), характеризующуюся шестью элементами: конечным множеством X входных сигналов (входным алфавитом); конечным множеством Y выходных сигналов (выходным алфавитом); конечным множеством Z внутренних состояний (внутренним алфавитом или алфавитом состояний); начальным состоянием z0, z0 Î Z; функцией переходов j (z, х) \ функцией выходов y (z, х). Автомат, задаваемый F-схемой: Абстрактный конечный автомат имеет один входной и один выходной каналы. В каждый момент t = 0, 1, 2,... дискретного времени F-автомат находится в определенном состоянии z(t) из множества Z состояний автомата, причем в начальный момент времени t = 0 он всегда находится в начальном состоянии z(0)=zo. В момент t, будучи в состоянии z(t), автомат способен воспринять на входном канале сигнал x(t)ÎX и выдать на выходном канале сигнал у(t) = y [z(t), x(t)], переходя в состояние z(t +1) = j [z(t), х(t)], z(t)ÎZ, y(t)ÎY. Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита X на множество слов выходного алфавита Y. Другими словами, если на вход конечного автомата, установленного в начальное состояние z0, подавать в некоторой последовательности буквы входного алфавита х(0), х(1), х(2),..., т. е. входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита у(0), у(1), у(2),..., образуя выходное слово. Таким образом, работа конечного автомата происходит по следующей схеме: в каждом i такте на вход автомата, находящегося в состоянии z(t), подается некоторый сигнал x(t), на который он реагирует переходом в (i + 1) -такте в новое состояние z(t + l) и выдачей некоторого выходного сигнала. По числу состояний различают конечные автоматы с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти (комбинационные или логические схемы) обладают лишь одним состоянием. При этом, работа комбинационной схемы заключается в том, что она ставит в соответствие каждому входному сигналу x(t) определенный выходной сигнал y(t), т. е. реализует логическую функцию вида
Эта функция называется булевой, если алфавиты X и Y, которым принадлежат значения сигналов х и у, состоят из двух букв. По характеру отсчета дискретного времени конечные автоматы делятся на синхронные и асинхронные. В синхронных F-автоматах моменты времени, в которые автомат «считывает» входные сигналы, определяются принудительно синхронизирующими сигналами. После очередного синхронизирующего сигнала с учетом «считанного» происходит переход в новое состояние и выдача сигнала на выходе, после чего автомат может воспринимать следующее значение входного сигнала. Таким образом, реакция автомата на каждое значение входного сигнала заканчивается за один такт, длительность которого определяется интервалом между соседними синхронизирующими сигналами. Асинхронный F-автомат считывает входной сигнал непрерывно, и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины х, он может несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдет в устойчивое, которое уже не может быть изменено данным входным сигналом. Чтобы задать конечный F-автомат, необходимо описать все элементы множества Существует несколько способов задания работы F-автоматов, но наиболее часто используются табличный, графический и матричный. Простейший табличный способ задания конечного автомата основан на использовании таблиц переходов и выходов, строки которых соответствуют входным сигналам автомата, а столбцы — его состояниям. При этом обычно первый слева столбец соответствует начальному состоянию z0. На пересечении i- й строки и k -го столбца таблицы переходов помещается соответствующее значение j(zk, хi,) функции переходов, а в таблице выходов — соответствующее значение y(zk, хi,) функции выходов. При другом способе задания конечного автомата используется понятие направленного графа. Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершины дуг графа, соответствующих тем или иным переходам автомата. При решении задач моделирования систем часто более удобной формой является матричное задание конечного автомата. При этом матрица соединений автомата есть квадратная матрица С=||сij||, строки которой соответствуют исходным состояниям, а столбцы — состояниям перехода. Необходимо отметить, что вообще на практике автоматы всегда являются асинхронными, а устойчивость их состояний обеспечивается тем или иным способом, например введением сигналов синхронизации. Однако на уровне абстрактной теории, когда конечный автомат выступает в виде математической схемы для формализации конкретных объектов без учета ряда второстепенных особенностей, часто удобно оказывается оперировать с синхронными конечными автоматами. Таким образом, понятие F-автомата в дискретно-детерминированном подходе к исследованию на моделях свойств объектов является математической абстракцией, удобной для описания широкого класса процессов функционирования реальных объектов в автоматизированных системах обработки информации и управления. В качестве таких объектов в первую очередь следует назвать элементы и узлы ЭВМ, устройства контроля, регулирования и управления, системы временной и пространственной коммутации в технике обмена информацией и т. д. Для всех перечисленных объектов характерно наличие дискретных состояний и дискретный характер работы во времени, т. е. их описание с помощью F-схем является эффективным. 61. Математические схемы в моделировании систем. P-схемы Исходной информацией при построении математических моделей процессов функционирования систем служат данные о назначении и условиях работы исследуемой (проектируемой) системы S. Эта информация определяет основную цель моделирования системы S и позволяет сформулировать требования к разрабатываемой математической модели М. Введение понятия «математическая схема» позволяет рассматривать математику не как метод расчета, а как метод мышления, как средство формулирования понятий, что является наиболее важным при переходе от словесного описания системы к формальному представлению процесса ее функционирования в виде некоторой математической модели (аналитической или имитационной). При пользовании математической схемой исследователя системы S в первую очередь должен интересовать вопрос об адекватности отображения в виде конкретных схем реальных процессов в исследуемой системе, а не возможность получения ответа (результата решения) на конкретный вопрос исследования. Математическую схему можно определить как звено при переходе от содержательного к формальному описанию процесса функционирования системы с учетом воздействия внешней среды, т. е. имеет место цепочка «описательная модель → математическая схема → математическая (аналитическая или (и) имитационная) модель». При построении математических моделей процессов функционирования систем можно выделить следующие основные подходы: · непрерывно-детерминированный (D-схемы); · дискретно-детерминированный (F-схемы); · дискретно-стохастический (Р-схемы); · непрерывно-стохастический (Q-схемы); · сетевой (N-схемы); · обобщенный или универсальный (А-схемы).
Определение: Вероятностный автомат [англ, probabilistic automat) (ВА) - это дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти нем и может быть описано статистически. Схемы вероятностных автоматов (Р-схем) применяются: · в проектировании дискретных систем, проявляющих статистически закономерное случайное поведение; · в определении алгоритмических возможностей систем; · в обосновании границ целесообразности их использования; · в решении задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворяющих заданным ограничениям. Математическое понятие Р-автомата формируется на понятиях, введенных для F-автомата. Пусть множество G, элементами которого являются всевозможные пары Введем более общую математическую схему. Пусть Ф — множество всевозможных пар вида (zk, yj), где yj — элемент выходного подмножества Y, т.е. Таблица 1
При этом Обозначим множество этих таблиц через В. Тогда четверка элементов Вероятностный автомат Мили Пусть элементы множества G индуцируют некоторые законы распределения на подмножествах Y и Z, которые можно представить соответственно в виде:
При этом Если для всех k и j имеет место соотношение Вероятностный автомат Мура Пусть выходной сигнал Р-автомата зависит лишь от того состояния, в котором находится автомат в данном такте работы, каждый элемент выходного подмножества Y индуцирует распределение вероятностей выходов, имеющее следующий вид: Таблица 3
Здесь Таблица 4
где pij – вероятность перехода автомата из состояния zi в состояние zj Можем записать Таблица выходов представлена следующим образом: Таблица 5
Первую из этих таблиц можно представить в виде квадратной матрицы размерности К x К, которая называется матрицей переходных вероятностей или просто матрицей переходов Р-автомата. В общем случае матрица переходов имеет вид
Для полного описания У-детерминированного Р-автомата необходимо задать начальное распределение вероятностей вида Таблица 6
где dK — вероятность того, что в начале работы автомат находится в состоянии zk При этом Будем предполагать, что до начала работы (до нулевого такта времени) Р-автомат всегда находится в состоянии z0, в нулевом такте времени меняет свое состояние в соответствии с распределением D. Дальнейшая смена состояний Р-автомата определяется матрицей переходов РР. Информацию о начальном состоянии Р-автомата удобно внести в матрицу РР/, увеличив ее размерность до
Описанный У-детерминированный Р-автомат можно задать в виде ориентированного графа, вершины которого сопоставляются состояниям автомата, а дуги — возможным переходам из одного состояния в другое. Дуги имеют веса, соответствующие вероятностям перехода рij, а около вершин графа пишутся значения выходных сигналов, индуцируемых этими состояниями. Y-детерминированные Р-автоматы могут использоваться как генераторы марковских последовательностей, которые необходимы при построении и реализации процессов функционирования систем S или воздействий внешней среды Е. Для оценки различных характеристик исследуемых систем, представляемых в виде Р-схем, кроме рассмотренного случая аналитических моделей можно применять и имитационные модели, реализуемые, например, методом статистического моделирования.
62. Математические схемы в моделировании систем. (N-схемы) Исходной информацией при построении математических моделей процессов функционирования систем служат данные о назначении и условиях работы исследуемой (проектируемой) системы S. Эта информация определяет основную цель моделирования системы S и позволяет сформулировать требования к разрабатываемой математической модели М. Введение понятия «математическая схема» позволяет рассматривать математику не как метод расчета, а как метод мышления, как средство формулирования понятий, что является наиболее важным при переходе от словесного описания системы к формальному представлению процесса ее функционирования в виде некоторой математической модели (аналитической или имитационной). При пользовании математической схемой исследователя системы S в первую очередь должен интересовать вопрос об адекватности отображения в виде конкретных схем реальных процессов в исследуемой системе, а не возможность получения ответа (результата решения) на конкретный вопрос исследования. Математическую схему можно определить как звено при переходе от содержательного к формальному описанию процесса функционирования системы с учетом воздействия внешней среды, т. е. имеет место цепочка «описательная модель → математическая схема → математическая (аналитическая или (и) имитационная) модель». При построении математических моделей процессов функционирования систем можно выделить следующие основные подходы: · непрерывно-детерминированный (D-схемы); · дискретно-детерминированный (F-схемы); · дискретно-стохастический (Р-схемы); · непрерывно-стохастический (Q-схемы); · сетевой (N-схемы); · обобщенный или универсальный (А-схемы).
Будем рассматривать N-схемы с использованием сетевой модели сети Петри. Сеть Петри представляет собой математическую модель для представления структуры и анализа динамики функциональной системы в терминах условия-события. Эта модель может служить для описания дискретно-математических систем таких как вычислительные процессы и программы, технические системы, информационные процессы. С помощью N-схемы можно моделировать параллельные конкурирующие процессы в различных системах. Моделировать порядок наступления событий в системе S произвольной длительности. Компоненты системы и их действия представлены абстрактными событиями, которые могут быть например: исполнение оператора программы, прерывания в системе, переход триггера из одного состояния в другое и т.д. Событие может быть реализовано 1 раз, повторятся многократно, порождая конкретное действия, или не произойти ни разу. Совокупность действий, возникшей как реализация событий при функции дискретной системы образуют процесс, порождаемый этой системой. Определенные сочетания условий разрешают реализовываться некоторому событию, так же как реальные события изменяют некоторые условия.
пример
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.9.7 (0.099 с.) |


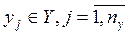
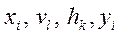 являются элементами непересекающихся подмножеств и содержат как детерминированные, так и стохастические составляющие.
являются элементами непересекающихся подмножеств и содержат как детерминированные, так и стохастические составляющие.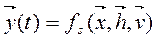 . Свойства системы в конкретный момент времени определяет состояние системы.
. Свойства системы в конкретный момент времени определяет состояние системы. (5.1)
(5.1)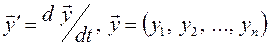 и
и  — n -мерные векторы;
— n -мерные векторы;  —вектор-функция, которая определена на некотором (n + 1) -мерном
—вектор-функция, которая определена на некотором (n + 1) -мерном 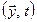 множестве и является непрерывной.
множестве и является непрерывной. . (5.2)
. (5.2) — вектор входных (задающих) воздействий;
— вектор входных (задающих) воздействий;  — вектор возмущающих воздействий;
— вектор возмущающих воздействий; 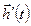 — вектор сигналов ошибки;
— вектор сигналов ошибки; 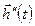 — вектор управляющих воздействий; независимые переменные:
— вектор управляющих воздействий; независимые переменные:  — вектор состояний системы S;
— вектор состояний системы S;  — вектор выходных s
— вектор выходных s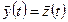 .
. ,— функционирует в дискретные моменты времени, которые называются такты, равные друг другу, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния.
,— функционирует в дискретные моменты времени, которые называются такты, равные друг другу, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния.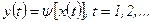
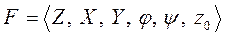 , т. е. входной, внутренний и выходной алфавиты, а также функции переходов и выходов, причем среди множества состояний необходимо выделить состояние z0, в котором автомат находился в момент времени t=0.
, т. е. входной, внутренний и выходной алфавиты, а также функции переходов и выходов, причем среди множества состояний необходимо выделить состояние z0, в котором автомат находился в момент времени t=0.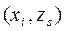 где xi и zs — элементы входного подмножества X и подмножества состояний Z соответственно
где xi и zs — элементы входного подмножества X и подмножества состояний Z соответственно 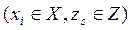 . Если существуют две такие функции
. Если существуют две такие функции 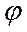 и
и 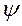 , то с их помощью осуществляются отображения
, то с их помощью осуществляются отображения  и
и  , то говорят, что
, то говорят, что  (1) определяет конечный автомат детерминированного типа.
(1) определяет конечный автомат детерминированного типа. . Пусть в любой элемент множества G индуцирует на множестве Ф некоторый закон распределения следующего вида:
. Пусть в любой элемент множества G индуцирует на множестве Ф некоторый закон распределения следующего вида: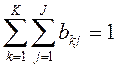 , (2) где bkj — вероятности перехода автомат в состояние zk и выдаче на выходе сигнала yj, если автомат был в состоянии z.S, и на его вход в момент времени поступил сигнал хi. Число таких распределений, представленных в виде таблиц, равно числу элементов множества G.
, (2) где bkj — вероятности перехода автомат в состояние zk и выдаче на выходе сигнала yj, если автомат был в состоянии z.S, и на его вход в момент времени поступил сигнал хi. Число таких распределений, представленных в виде таблиц, равно числу элементов множества G.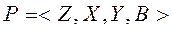 (3) называется вероятностным автоматом (Р-автоматом).
(3) называется вероятностным автоматом (Р-автоматом).
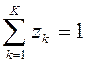 и
и 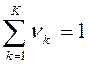 (4)— вероятности перехода Р-автомата в состояние zk и выдачи выходного сигнала yk при условии, что Р-автомат находился в состоянии zS и на его вход поступил входной сигнал xt.
(4)— вероятности перехода Р-автомата в состояние zk и выдачи выходного сигнала yk при условии, что Р-автомат находился в состоянии zS и на его вход поступил входной сигнал xt.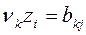 (5), то такой автомат называется вероятностным автоматом Мили. Представленное требование означает выполнение условия независимости распределений для нового состояния Р-автомата и его выходного сигнала.
(5), то такой автомат называется вероятностным автоматом Мили. Представленное требование означает выполнение условия независимости распределений для нового состояния Р-автомата и его выходного сигнала.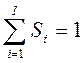 ,(6) где Si, — вероятность появления сигнала на выходе yi при условии, что Р-автомат находился в состоянии zk. Частным случаем Р-автомата являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминированно. Такой автомат называется Y-детерминированным вероятностным автоматом. Если состояние Р-автомата определяется детерминировано, то такой автомат называется Z-детерминированным вероятностным автоматом. Аналогично, Z-детерминированным вероятностным автоматом называется Р-автомат, у которого выбор нового состояния является детерминированным. Рассмотрим пример У-детерминированного Р-автомата. Пусть У-детерминированный Р-автомат, задан таблицей переходов
,(6) где Si, — вероятность появления сигнала на выходе yi при условии, что Р-автомат находился в состоянии zk. Частным случаем Р-автомата являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминированно. Такой автомат называется Y-детерминированным вероятностным автоматом. Если состояние Р-автомата определяется детерминировано, то такой автомат называется Z-детерминированным вероятностным автоматом. Аналогично, Z-детерминированным вероятностным автоматом называется Р-автомат, у которого выбор нового состояния является детерминированным. Рассмотрим пример У-детерминированного Р-автомата. Пусть У-детерминированный Р-автомат, задан таблицей переходов (7)
(7) (8)
(8) . (9)
. (9)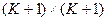 (10). При этом первая строка такой матрицы, сопоставляемая состоянию z0, будет иметь вид (0, dt, d2,......, dK), а первый столбец будет нулевым.
(10). При этом первая строка такой матрицы, сопоставляемая состоянию z0, будет иметь вид (0, dt, d2,......, dK), а первый столбец будет нулевым. - сопоставляется со состоянием z0 (11)
- сопоставляется со состоянием z0 (11)
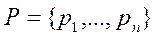 -конечное множество позиций сети Петри
-конечное множество позиций сети Петри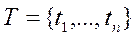 -конечное множество переходов
-конечное множество переходов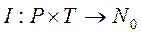 входная функция перехода
входная функция перехода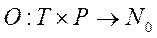 выходная функция перехода
выходная функция перехода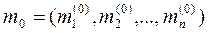 вектор, каждая маркировка которая соответствует позиции Сети Петри(СП).
вектор, каждая маркировка которая соответствует позиции Сети Петри(СП).
 ,
,