
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование операционных системСодержание книги
Поиск на нашем сайте
За организацию обработки информации в компьютерной системе отвечает ОС, которая распределяет ресурсы и руководит процессами распределения этих ресурсов между программами, выполняемыми компьютером. К этим программам принадлежат не только программы пользователей, но и системные программы ОС. Ресурсы ОС – это различные устройства (процессор, дисплей, клавиатура, накопители на магнитных дисках, модемы, принтеры и т.д.), А также память, файлы, программные модули. В случае занятости нужного ресурса, который требует программа, к нему создается очередь. Таким образом, если программы пользователей, которые выполняются компьютером, используют одинаковые ресурсы в некоторые промежутки времени, то выполнение таких программ будет существенно задерживаться. Типичные функции ОС: выбор программы, которая будет выполняться процессором, управление общей памятью, управление операциями ввода-вывода, обработка прерываний. Компьютерная система обычно работает в мультипрограммном или в многозадачном режиме. Классический мультипрограммный режим построен на принципе совместимости операций, которые выполняет процессор, и операций ввода-вывода, которые выполняет программируемый контроллер или процессор ввода-вывода. Например, если компьютер выполняет вывод на печать результатов некоторой программы, то пользователь одновременно может выполнять другую программу. Многозадачный режим построен на принципе распределения времени работы процессора между несколькими выполняемыми программами. Для каждой программы выделяется свой промежуток времени (квант времени), в течение которого она выполняется процессором. Если за это время программа не закончилась, то она прерывается, и процессор начинает выполнять другую программу. Обычно прерванная программа становится в очередь к процессору последней. Таким образом, каждая выполняемая программа несколько раз получает процессорное время для расчетов до того как покидает компьютер. Если программа во время выполнения процессором прерывается для операций ввода-вывода (например, для записывания информации на диск), то она выводится из очереди к процессору, пока не закончит операцию записывания. Остаток процессорного времени от кванта не сохраняется, и по окончании операции записывания эта программа, когда ей будет предоставлен процессор, получает новый квант времени.
При моделировании режима распределения времени процессора возникает задача о назначении промежутков времени для определенных групп программ пользователей. Использование режима распределения времени содействует тому, что более короткие задания пользователей выполняются раньше, поскольку они набирают необходимое количество квантов процессорного времени быстрее, чем длинные задания. Это вынуждает пользователей делать задания для выполнения компьютером более короткими по времени выполнения. Если взять очень маленький квант времени, то программы пользователей будут очень часто прерываться, А каждое прерывание требует определенного времени на его обработку компьютером. Если квант времени будет стремиться к бесконечности, то программы будут обрабатываться процессором по принципу «первая поступила – первая выполняется». В любом режиме работы (мультипрограммном или многозадачном) компьютер c одним процессором в каждый момент времени выполняет только одну программу (одну команду). Если используется мультипроцессорная система c несколькими одинаковыми процессорами, то становится возможным выполнения нескольких программ на разных процессорах. Большей частью такая система моделируется как многоканальная CMO в отличие от CMO c одним устройством обслуживания, которая моделирует работу однопроцессорной системы. Таким образом, работу компьютерной системы, управляемой ОС, можно представить в упрощенном виде как работу сети CMO. При моделировании обычно интересуются временем пребывания программы пользователя в компьютерной системе (от ввода программы или запроса на ее выполнение до получения результатов ее работы или ответа) или числом программ, выполненных системой за единицу времени. Типичная программа или запрос пользователя может описываться: идентификатором программы, временем поступления в систему, емкостью нужной памяти, количеством запросов к устройствам ввода-вывода и распределением их по времени, количеству данных, которые вводятся и выводятся на тех или иных устройствах, А также более детальной информацией в зависимости от цели моделирования.
74. Интерпретация результатов моделирования. Статистические оценки. Статистические гипотезы. В последние годы заметен значительный рост интенсивности исследований в области моделирования и искусственного интеллекта, что определяет основные тенденции в развитии технологии создания систем поддержки принятия решений (СППР). Сегодня моделирование - наиболее широко используемый прием решения задач планирования и управления.
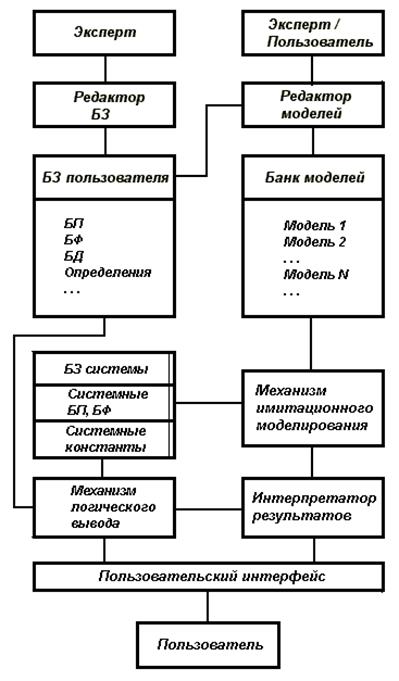
Однако, несмотря на рост популярности и перспективность использования моделирования на практике, имеются существенные трудности в его практической реализации. Проблемы разработки моделей и оценки их адекватности хорошо освещены в литературе [1]. Другой проблемой, сопровождающей любую задачу моделирования, является объяснение результатов моделирования, поскольку моделирование не дает практического решения, а лишь позволяет получить последовательность фактов во времени и выработать некоторые предложения. Интерпретация фактов и получение выводов на ее основе лежит вне сферы задач моделирования. Тем не менее интерпретация и получение выводов критически важны для пользователя комплекса моделей (КМ). Эту проблему осложняет возникающая в ряде случаев потребность привлечения экспертов для интерпретации результатов моделирования. Отсутствие экспертов требуемой квалификации или высокая стоимость экспертизы результатов моделирования могут создать серьезные препятствия и даже нивелировать преимущества моделирования как инструмента планирования и управления. Таким образом, актуальной задачей является разработка специальных программных сред, ориентированных на проведение консультаций и объяснения результатов имитационного моделирования. В статье рассматриваются принципы построения разработанной СППР и способ интерпретации фактов, используемых при имитационном моделировании, основанной на технологии ЭС. Организация знаний и алгоритм логического вывода в СППР На Рис показана обобщенная схема интегрированной СППР, совмещающей способности моделирования процессов и получения выводов по результатам моделирования с использованием технологии ЭС.
Система поддержки принятия решений оснащена двумя редакторами (см. Рис.1), основными функциями которых являются оказание сервиса пользователю в формированиях базы знаний (БЗ), состоящей из базы фактов (БФ) и базы правил (БП), или моделирующих модулей, удовлетворяющих синтаксическим требованиям СППР. Банк моделей является библиотекой созданного пользователем комплекса моделей, к которым организуется доступ при консультациях с пользователем. Моделирующий модуль формирует сценарий, позволяющий при имитации событий получить траекторию моделируемой системы в фазовом пространстве, представляемую в виде времен совершения событий или значений параметров, которые фиксируются в БЗ системы, придавая СППР прогнозирующие способности. БЗ системы, помимо этого, включает в себя данные о системных константах, не зависящих от моделируемых значений времен или параметров. Интерпретатор результатов контролирует работу механизма имитационного моделирования и механизма логического вывода (МЛВ) и взаимодействует с пользователем с целью объяснения результатов работы и контроля состояния системы.
Особенностью задачи интерпретации результатов моделирования является потребность в сохранении информации о всех изменениях состояний элементов моделируемой системы в процессе эксперимента. Классические ЭС (например, продукционного типа) ориентированы на получение одного логического вывода за один акт работы МЛВ и не могут выдать информацию о достоверности всех других менее достоверных, но возможных выводов. Поэтому их использование для анализа всех свершившихся событий в моделируемой системе проблематично.
В рассматриваемой СППР выбран альтернативный подход к построению МЛВ, использующий алгоритм решения задачи линейного программирования (ЛП). Один из возможных способов реализации такого подхода на базе алгоритма целочисленного ЛП описан в литературе [2, 3]. Отличие использованного в СППР способа построения МЛВ - сведение БП к задаче ЛП общего вида, что обеспечивает большую гибкость процессам интерпретации благодаря введению элементов "размытой" логики. Таблица 1 В Табл.1 представлены формальные правила (см. комментарий) преобразования БП в систему линейных выражений, где Рx, РА, РАi - степень уверенности в совершении событий Х, А, Aj; Ui ([0, 1] - степень уверенности в том, что i-тое логическое выражение неверно. Существуют только два случая (полное название и полная уверенность пользователя), когда UiI = 0. В первом случае логическое выражение - цель логического вывода и соответствует событию, достоверность которого пользователь не может априорно оценить. Во втором случае логическое выражение соответствует событию, определяющему условия имитационного моделирования с достоверностью свершения, равной единице.
Соответствие логических и линейных выражений Логическое выражение Линейное выражение (Х) -> (Истина) PX <= 1 ± U1 (Х) -> (Ложь) PX <= U2 (Х) -> не (А) PX + PA <= 1 ± U3 (Х) -> (А1 и А2 и…Аn) PX <= PAj ± U4j, для всех j (А1 и А2 и…Аn) -> (X) - PX + SUMj (PAj) <= n – 1 ± U5 (Х) -> (А1 или А2 или…Аn) PX - SUMj (PAj) <= ± U6 (А1 или А2 или…Аn) -> (X) - PX + PAj <= ± U7j, для всех j
Ядром рассматриваемого МЛВ является целевая функция: SUMi (Gi * Pi) > min, обеспечивающая выработку рекомендаций по коррекции оценок достоверности свершения событий. Здесь Gi - индикатор уверенности в i-ом логическом выражении (Gi = 0, если Ui = 1; Gi = 1 в других случаях), задаваемый экспертно или вычисляемый по данным, хранящимся в БП системы; Pi - уверенность в i-ом логическом выражении.
В случае использования симплекс-метода для решения задач ЛП величины dPi= 1- Pi для Pi, соответствующих фиктивным переменным, вводимым в правую часть линейных выражений для приведения их к стандартной форме, будут служить рекомендациями по корректировке исходной системы предположений о достоверности свершения событий.
Справедливость последнего утверждения подтверждают следующие рассуждения.
При вероятностной интерпретации вводимых фактов формирующаяся система знаний должна обладать свойством полной группы событий, что мало вероятно при экспертном задании оценок достоверности. Описанный МЛВ позволяет для первой задачи получить рекомендации в виде приращений?PI по корректировке допущений пользователя о достоверности событий и добиться выполнения условия нормировки. При этом значение целевой функции задачи ЛП будет являться мерой некорректности всей системы знаний, событий. Далее раскрывается содержание основных этапов решения задачи интерпретации фактов, используемых при имитационном моделировании. Сценарий интерпретации данных Интерпретация входных фактов Формирование временной БП, содержащей в себе правила типа (Х)=>(Истина) или (Х)=>(Ложь) только для событий (Х), являющихся исходными данными для имитационного моделирования. Признак такого события - неравенство нулю значения априорной степени уверенности в правиле. С использованием МЛВ для временной БП получение рекомендаций в виде значений dPi по корректировке предположений о достоверности правил во временной БП. Воспроизведение на экране объяснения логического вывода. После корректировки пользователем исходной БП может быть произведена повторная интерпретация входных фактов. При этом устраняется противоречивость исходных предположений пользователя о достоверности совершения исходных событий. Интерпретация выходных фактов Формирование временной БП, содержащей в себе правила типа (Х)=>(Истина) или (Х)=>(Ложь) только для событий, априорная достоверность свершения которых равна нулю. С использованием МЛВ для временной БП получение рекомендаций в виде значений dPi по корректировке предположений о достоверности правил по временной БП. Воспроизведение на экране объяснения логического вывода. При этом полагается, что СППР осуществляет ввод в БФ и БП фактов, аналогичных первой задаче, а события, достоверность которых пользователь желает оценить, вводятся как абсолютно недостоверные события (т.е. искусственно нарушается свойство нормировки для полной группы событий в исходной БП). Интерпретация свершившихся событий Получение рекомендаций в виде значений PI для исходной БП по корректировке значений апостериорных степеней уверенности а правилах. Воспроизведение на экране объяснения логического вывода.
Интерпретация потребностей ЛРП Корректировка ЛРП значений апостериорных степеней уверенности в БП с целью указания потребностей в изменении результатов имитационного моделирования. Этапы, аналогичные задаче 2.
Интерпретация рекомендаций Замена в БП значений априорных степеней уверенности значениями скорректированных в задаче 4 апостериорных степеней уверенности.
Этапы, аналогичные задаче 3.
Отличием результата, получаемого в данном случае, от результата, получаемого в задаче 2, является то, что рекомендации?Pi будут иметь отношение к входным данным. Стат. Оценки Статистические оценки, функции от результатов наблюдений, употребляемые для статистического оценивания неизвестных параметров распределения вероятностей изучаемых случайных величин. Например, если X1,..., Xn - независимые случайные величины, имеющие одно и то же нормальное распределение с неизвестным средним значением а, то функции - среднее арифметическое результатов наблюдений
и выборочная медиана m = m(X1,..., Xn) являются возможными точечными Статистические оценки неизвестного параметра а. В качестве Статистические оценки какого-либо параметра q естественно выбрать функцию q*(X1,..., Xn) от результатов наблюдений X1,..., Xn, в некотором смысле близкую к истинному значению параметра. Принимая какую-либо меру «близости» Статистические оценки к значению оцениваемого параметра, можно сравнивать различные оценки по качеству. Обычно мерой близости оценки к истинному значению параметра служит величина среднего значения квадрата ошибки
(выражающаяся через математическое ожидание оценки E0q* и её дисперсию D0q*). В классе всех несмещённых оценок (для которых E0q* = 0) наилучшими с этой точки зрения будут оценки, имеющие при заданном n минимальную возможную дисперсию при всех q. Указанная выше оценка Х для параметра а нормального распределения является наилучшей несмещенной оценкой, поскольку дисперсия любой другой несмещенной оценки а* параметра а удовлетворяет неравенству, где s2 - дисперсия нормального распределения. Если существует несмещенная оценка с минимальной дисперсией, то можно найти и несмещенную наилучшую оценку в классе функций, зависящих только от достаточной статистики. Имея в виду построение Статистические оценки для больших значений n, естественно предполагать, что вероятность отклонений q* от истинного значения параметра q, превосходящих какое-либо заданное число, будет близка к нулю при n ®¥. Статистические оценки с таким свойством называются состоятельными оценками. Несмещенные оценки, дисперсия которых стремится к нулю при n ®¥, являются состоятельными. Поскольку скорость стремления к пределу играет при этом важную роль, то асимптотическое сравнение Статистические оценки производят по отношению их асимптотической дисперсии. Так, среднее арифметическое Х в приведённом выше примере - наилучшая и, следовательно, асимптотически наилучщая оценка для параметра а, тогда как выборочная медиана m, представляющая собой также несмещенную оценку, не является асимптотически наилучшей, т.к.
(тем не менее использование m имеет также положительные стороны: например, если истинное распределение не является в точности нормальным, а несколько отличается от него, дисперсия Х может резко возрасти, а дисперсия m остаётся почти той же, т. е. m обладает свойством, называется «прочностью»). Одним из распространённых общих методов получения Статистические оценки является метод моментов, который заключается в приравнивании определённого числа выборочных моментов к соответствующим моментам теоретического распределения, которые суть функции от неизвестных параметров, и решении полученных уравнений относительно этих параметров. Хотя метод моментов удобен в практическом отношении, однако Статистические оценки, найденные при его использовании, вообще говоря, не являются асимптотически наилучшими, Более важным с теоретической точки зрения представляется максимального правдоподобия метод, который приводит к оценкам, при некоторых общих условиях асимптотически наилучшим. Частным случаем последнего является наименьших квадратов метод. Метод Статистические оценки существенно дополняется оцениванием с помощью доверительных границ. Стат. Гипотезы Пусть в (статистическом) эксперименте доступна наблюдению случайная величина X, распределение которой Статистическая гипотеза, однозначно определяющая распределение Статистическая гипотеза, утверждающая принадлежность распределения
На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу H0. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза H1, называемая конкурирующей или альтернативной.
Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу.
В большинстве случаев статистические критерии основаны на случайной выборке фиксированного объема из распределения. В последовательном анализе выборка формируется в ходе самого эксперимента и потому ее объем является случайной величиной (см. Последовательный статистический критерий). Пример Пусть дана независимая выборка Этапы проверки статистических гипотез Формулировка основной гипотезы H0 и конкурирующей гипотезы H1. Гипотезы должны быть чётко формализованы в математических терминах. Задание вероятности α, называемой уровнем значимости и отвечающей ошибкам первого рода, на котором в дальнейшем и будет сделан вывод о правдивости гипотезы. Расчёт статистики φ критерия такой, что: её величина зависит от исходной выборки
по её значению можно делать выводы об истинности гипотезы H0; сама статистика φ должна подчиняться какому-то известному закону распределения, т.к. сама φ является случайной в силу случайности Построение критической области. Из области значений φ выделяется подмножество Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику φ и по попаданию (или непопаданию) в критическую область Виды критической области
Выделяют три вида критических областей: Двусторонняя критическая область определяется двумя интервалами Левосторонняя критическая область определяется интервалом Правосторонняя критическая область определяется интервалом
75. Планирование экспериментов с моделью. Проведение экспериментов с моделью в GPSS. Стратегическое планирование Цели моделирования достигаются путем исследования разработанной модели. Исследования заключаются в проведении экспериментов по определению выходных характеристик системы при разных значениях управляемых переменных параметров модели. Эксперименты следует проводить по определенному плану. Особо важным является планирование экспериментов при численном и статистическом моделировании. Это обусловлено большим числом возможных сочетаний значений управляемых параметров, а каждый эксперимент проводится при определенном сочетании значений параметров. Например, при пяти управляемых параметрах, имеющих по три значения, количество сочетаний параметров равно 243, при десяти параметрах по пять значений, число сочетаний приближается к 10 млн. Поэтому возникает необходимость в выборе определенных сочетаний параметров и последовательности проведения экспериментов. Это называется стратегическим планированием. Разработка плана начинается на ранних этапах создания модели, когда выявляются характеристики качества и параметры, с помощью которых предполагается управлять качеством функционирования системы. Эти параметры называют факторами. Затем выделяются возможные значения количественных параметров и варианты качественных (функциональных) параметров. Их называют уровнями. При этом число сочетаний, где - число факторов. Если число факторов велико, то для проведения исследований системы используется один из методов составления плана по неполному факторному анализу. Эти методы хорошо разработаны в теории планирования экспериментов.
Тактическое планирование Совокупность методов уменьшения длительности машинного эксперимента при обеспечении статистической достоверности результатов имитационного моделирования получила название тактического планирования. На длительность одного эксперимента (периода моделирования) влияет степень стационарности системы, взаимозависимости характеристик и значения начальных условий моделирования. Данные, собранные в эксперименте, можно рассматривать как временные ряды, состоящие из замеров определенных характеристик. Ряд замеров характеристики может рассматриваться как выборка из стохастической последовательности. Если эта последовательность стационарна, ее среднее не зависит от времени. Оценкой является среднее по временному ряду. Для эргодической последовательности точность этой оценки возрастает с ростом.
Если заданы максимальная допустимая ошибка оценки (доверительный интервал) и минимальная вероятность того, что истинное среднее лежит внутри этого интервала, то существует минимальный размер исследуемой выборки. Этот размер соответствует минимальной длительности эксперимента. Для оценки нескольких характеристик период моделирования определяется по максимальному значению. Система GPSS World – это мощная среда компьютерного моделирования общего назначения, разработанная для профессионалов в области моделирования. Это комплексный моделирующий инструмент, охватывающий области как дискретного, так и непрерывного компьютерного моделирования, обладающий высочайшим уровнем интерактивности и визуального представления информации. GPSS World является наиболее современной реализацией языка GPSS, дополненной вспомогательным языком PLUS. GPSS World включает в себя 53 типа блоков и 25 команд, большое количество системных числовых атрибутов. Кроме того, 12 типов операторов составляют язык PLUS – Programming Language Under Simulation. Эффективность PLUS во многом обеспечивается большой библиотекой процедур. GPSS World является объектно-ориентированным языком. В совокупность его объектов входят объекты «Модель», «Процесс моделирования», «Отчет» и текстовые объекты. • Объект «Модель» - главным образом содержит операторы модели, а также набор встроенных настроек. Кроме того, включает в себя закладки и циркулярный список синтаксических ошибок. • Объект «Процесс моделирования» создаются при трансляции операторов объекта «Модель». После этого для изменения его состояния применяются команды. Эти команды могут входить в объект «Модель» или передаваться объекту «Процесс моделирования» в интерактивном режиме. • Объект «Отчет». Одной из самых сильных сторон GPSS всегда были стандартные отчеты. По существу без усилий со стороны разработчика модели по завершению моделирования автоматически создается отчет обо всех объектах GPSS, содержащихся в модели. • Текстовый объект – это способ представления обычного текстового файла в GPSS World. В основном они используются совместно с командами INCLUDE для подключения некоторого набора операторов, используемого в различных моделях. Кроме того, закрепив команду INCLUDE за горячей клавишей, можно интерактивно передавать объекту «Процесс моделирования» целые списки управляющих команд. В языке GPSS было сделано большое количество изменений. А именно: • Новые команды, блоки и СЧА; • Полиморфные типы данных; • Отсутствие нумерации строк; • Многомерные матрицы (до 6 измерений); • Отсутствие автоматического округления промежуточных результатов; • Вспомогательный язык PLUS; • Процедура дисперсионного анализа ANOVA. 1) Полиморфные типы данных Переменные могут принимать значения одного из четырех типов. Ячейки, элементы матриц, параметры транзактов и переменные пользователя могут принимать целочисленное, вещественное, строковое и неопределенное значение. Значения времени могут быть целыми и вещественными. Преобразование типов происходит автоматически. Для работы со строковыми значениями в библиотеке процедур присутствует ряд специальных функций. Неопределенные значения используются при проведении дисперсионного анализа. 2) Новые команды • CONDUCT – Выполнение экспериментов; • EXIT – Выход из GPSS World с возможностью сохранения; • INTEGRATE – Автоматическое вычисление интеграла для переменной пользователя; • INCLUDE – Подключение к модели дополнительных файлов. 3) Новые блоки • ADOPT – Изменение номера семейства; • DISPLACE – Перемещение транзакта; • INTEGRATION – Включение/выключение интегрирования переменной; • PLUS – Вычисление PLUS-выражения; • OPEN, CLOSE, READ, WRITE, SEEK – Блоки управления потоками данных. 4) PLUS Язык PLUS является встроенным в GPSS World языком программирования и предназначен для удовлетворения потребностей пользователей в управлении данными, особых вычислительных алгоритмах и других операциях, которые не могут быть обеспечены средствами операторов и команд GPSS. Новый блок PLUS позволяет вызывать PLUS-процедуру, которая выполняется как любой другой блок GPSS. Это позволяет создавать собственные блоки с очень сложной структурой. Кроме того, выражения, записанные с помощью синтаксиса языка PLUS (так называемые PLUS-выражения) могут использоваться в качестве операндов блоков и команд. И выражения могут содержать вызовы встроенных процедур или процедур пользователя. Язык PLUS включает в себя следующие операторы: • Оператор присваивания; • Вызов процедуры; • BEGIN; • DO…WHILE; • END; • EXPERIMENT; • GOTO; • IF…THEN…ELSE; • PROCEDURE; • RETURN; • TEMPORARY. EXPERIMENT – Этот оператор предназначен для определения специальной процедуры пользователя, которая управляет несколькими повторяющимися процессами моделирования. Другими словами, оператор EXPERIMENT применяется для проведения экспериментов. Экспериментам посвящен отдельный раздел моего доклада. PROCEDURE – Оператор PROCEDURE используется для определения процедур пользователя. Процедуры обладают глобальной областью действия, т.е. могут вызываться в любом месте модели. TEMPORARY – Это оператор, предназначенный для создания временных переменных пользователя и матриц, существующих только во время выполнения процедуры. По завершении работы процедуры все временные переменные и матрицы уничтожаются.
5) Встроенная библиотека процедур GPSS World содержит большую встроенную библиотеку PLUS-процедур, которые обеспечивают работу с потоками данных, различные манипуляции со строками, математические операции и позволяют задавать вероятностные распределения. В библиотеку процедур GPSS World входят: • служебные процедуры (DoCommand, ANOVA, Exit); • математические процедуры; • процедуры запроса состояния транзактов; • процедуры обработки строк; • процедуры управления потоками данных; • процедуры динамического вызова; • вероятностные распределения.
6) Проведение экспериментов и дисперсионный анализ Концептуально GPSS World обеспечивает проведение экспериментов 3 типов: • отсеивающие эксперименты – используются для определения наиболее важных факторов, влияющих на моделируемую систему; • оптимизирующие эксперименты – позволяют определить оптимальные уровни факторов; • эксперименты пользователя – эксперименты над моделью, программируемые пользователем.
Для быстрого задания и проведения отсеивающих и оптимизирующих экспериментов GPSS World предоставляет автоматические генераторы этих экспериментов. Они позволяют быстро определить условия проведения эксперимента с помощью диалоговых окон. Завершающий шаг любого эксперимента – это, как правило, анализ результатов. При использовании процедуры дисперсионного анализа ANOVA большая часть работы выполняется без участия пользователя. Она позволяет осуществлять многофакторный дисперсионный анализ, рассматривающий до 6 факторов и трехфакторные произведения всех основных факторов. 76. Моделирование при исследовании и проектировании автоматизированных систем обработки информации и управления При построении моделей процессов, происходящих в сложных производственных системах, при описании их структуры, оценке эффективности и оптимизации этих систем используются различные аналитические и имитационные схемы математического моделирования. Известно, что построение аналитической модели функционирования производства является очень трудоемким и часто не реализуемым процессом (Вавилов, 1983). Единственным выходом в такой ситуации становится метод имитационного моделирования, основанный на моделирующих алгоритмах, которые строятся с использованием различных стандартов, зачастую включая в себя обобщенные методы исследования систем. Одним из таких методов является моделирование систем массового обслуживания. Современные производственные системы отличаются сложной структурой потоков (например, с множеством последовательно-параллельных технологических этапов, наличием разнообразного оборудования, многообразием видов продукции и т.д.) (Кузнецов, Бурцев, 1998). Каждому этапу потока соответствует определенный объект производства. Совокупность взаимодействий между ними отражается отношениями, которые могут иметь различный характер. Типичным примером такого производства является технологический процесс металлургического предприятия. Действительно, процесс металлургического производства представляет собой многофазную систему массового обслуживания, в которой поток требований на обработку соответствует некоторой партии единиц продукции, дисциплина ожидания - механизмы функционирования складов продукции, а дисциплина обслуживания характеризуется технологией обработки продукции в агрегатах. В общем случае любой производственный процесс характеризуется отсутствием полной закономерности в функционировании с наличием множества случайных составляющих: время обработки единицы продукции, длительность безотказной работы агрегатов и механизмов, время простоев и восстановительных работ и т. д. Поэтому, при моделировании сложных производств возникает необходимость рассматривать статистические модели систем массового обслуживания разных классов. Сущность метода имитационного моделирования применительно к задачам массового обслуживания состоит в следующем. Строятся алгоритмы, при помощи которых можно вырабатывать потоки требований заданной интенсивности, а также моделировать процессы функционирования обслуживающих систем. Эти алгоритмы используются для многократного воспроизведения при фиксированных условиях задачи, а получаемая при этом информация подвергается статистической обработке для оценки величин, являющихся показателями качества обслуживания. Современное развитие вычислительных средств практически не накладывает ограничений на сложность реализуемых моделирующих алгоритмов. Проблемы, с которыми приходится иметь дело, связаны с увеличением трудоемкости построения моделей (от формального описания объектов системы и взаимодействия между ними, программирования моделирующих алгоритмов до выдачи результатов, проверки адекватности и документирования модели). Это обстоятельство не способствует оперативному использованию результатов имитационных экспериментов, снижает рентабельность самого процесса моделирования, сужает сферу практического применения имитационных моделей. Радикальным способом решения этих проблем является автоматизация процедур, охватывающих проектирование, построение и реализацию моделей. В настоящее время реальным средством достижения желаемого результата является применение многофункциональных объектно-ориентированных систем автоматизированного моделирования и проектирования. Поэтому является целесообразным разработать общие принципы и универсальную программную среду для моделирования производственных процессов. Используя основные положения теории массового обслуживания, методов объектно-ориентированного проектирования и программирования на кафедре АСУ Липецкого государственного технического университета была разработана система автоматизированного моделирования сложных производственных процессов, которая повышает оперативность принятия решения, снижает требования к подготовке пользователя по программированию, теории систем, сокращает трудоемкость и п
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 344; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.26 (0.013 с.) |

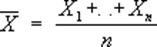
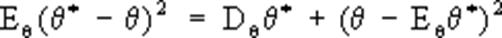
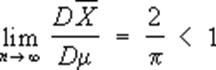
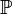 неизвестно полностью или частично. Тогда любое утверждение, касающееся
неизвестно полностью или частично. Тогда любое утверждение, касающееся 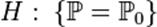 , где
, где 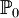 какой-то конкретный закон, называется простой.
какой-то конкретный закон, называется простой.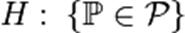 , где
, где 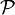 - семейство распределений, называется сложной.
- семейство распределений, называется сложной.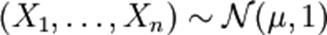 из нормального распределения, где μ — неизвестный параметр. Тогда
из нормального распределения, где μ — неизвестный параметр. Тогда 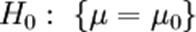 , где μ0 — фиксированная константа, является простой гипотезой, а конкурирующая с ней
, где μ0 — фиксированная константа, является простой гипотезой, а конкурирующая с ней 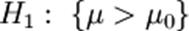 — сложной.
— сложной.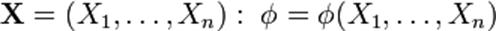 ;
;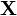 .
.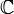 таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство
таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство 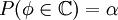 . Это множество и называется критической областью.
. Это множество и называется критической областью.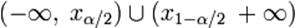 , где
, где 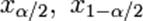 находят из условий
находят из условий 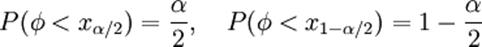 .
.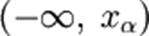 , где xα находят из условия P(φ < xα) = α.
, где xα находят из условия P(φ < xα) = α.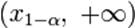 , где x1 − α находят из условия P(φ < x1 − α) = 1 − α.
, где x1 − α находят из условия P(φ < x1 − α) = 1 − α.


