Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмы вычисления сумм бесконечных рядовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В этих алгоритмах производится суммирование последовательно вычисляемых членов ряда. Сходство таких алгоритмов с предыдущим заключается в том, что вычисление каждого следующего члена ряда производится по значению предыдущего. Вычисление суммы имеет смысл только в том случае, если ряд сходится, то есть значения членов ряда постепенно уменьшаются. Накопление суммы производят до тех пор, пока очередной член ряда не станет меньше некоторого, наперед заданного, достаточно малого числа. В качестве примера рассмотрим алгоритм вычисления синуса некоторого числа. Синус можно представить как сумму бесконечного ряда 5.2.
Особенность данного ряда состоит в том, что каждый член ряда, начиная со второго, может быть найден их предыдущего по формуле 5.3.
Алгоритм вычисления синуса по формуле 5.2 с использованием соотношения 5.3 представлен на рисунке 5.6. В рассмотренном алгоритме, помимо основного цикла для накопления суммы ряда, есть еще дополнительный цикл. В этом цикле переменная х уменьшается каждый раз на величину периода синуса, который равен 2π. Цикл работает до тех пор, пока х не станет меньше, чем 2π. Это сделано для того, чтобы избежать переполнения или потери значащих цифр при больших значениях х. Ряд 5.2 при больших значениях х сходится медленно, а факториал и «х в степени» растут очень быстро. Это приводит к тому, что все значащие цифры этих чисел перестают помещаться в разрядной сетке и, следовательно, обрезаются, вследствие чего результат искажается. 5.1.6.1 Задание для самостоятельной работы В рамках выполнения лабораторной работы студент должен самостоятельно разработать алгоритм вычисления суммы сходящегося бесконечного ряда в соответствии со своим вариантом задания. Варианты задания приведены в таблице 5.2. Номер варианта выбирается в соответствии с последней цифрой зачетной книжки.
Рисунок 5.6 – Алгоритм вычисления синуса
5.2 Создание проекта WhileRepeat В этом проекте студент должен реализовать разработанные выше алгоритмы решения уравнения методом итераций и вычисления суммы бесконечного ряда, требующие использования инструкций while…do или repeat…until. В качестве образца мы будем рассматривать создание проекта для вычисления кубического корня методом итерации и вычисления значения функции синус путем нахождения суммы бесконечного ряда. Алгоритмы этих вычислений рассматривались выше. Задача студента – реализовать подобным образом алгоритмы, соответствующие его варианту.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 661; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.131.115 (0.006 с.) |

 (5.2)
(5.2) (5.3)
(5.3)

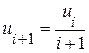


 , для х<1
, для х<1


 , для х<1
, для х<1

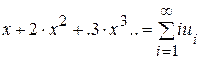
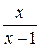

 , для х>1
, для х>1