Анализ передачи параметров по наименованию

Настройте режим пошагового выполнения процедуры для вычисления корней уравнения и проанализируйте значения коэффициентов уравнения до и после вызова процедуры getKoef.

Уберите префикс var в списке параметров процедуры getKoef и снова проанализируйте значения коэффициентов уравнения до и после вызова процедуры getKoef.

Восстановите заголовок процедуры.

Сделайте вывод и зафиксируйте в отчете.

Анализ передачи параметров по значению

Измените функцию расчета по формуле таким образом, чтобы после вычисления результата значения формальных параметров изменялись, например, становились нулями.

Проверьте в пошаговом режиме, будут ли меняться значения фактических параметров после обращения к измененной функции.

Восстановите текст функции.

Сделайте вывод и зафиксируйте в отчете.

3.4 Содержание отчета

– Наименование работы.

– Цель работы.

– Краткое описание понятий процедура и функция.

– Перечень возможных вариантов расположения подпрограмм и влияние расположения на видимость подпрограмм.

– Способы передачи параметров в подпрограммы.

– Тексты своих процедур setKoef и getKoef.

– Текст дополнительного модуля для своей формулы.

– Расчетная формула и контрольные примеры.

– Результаты тестирования проекта на контрольных примерах в виде копии экрана с протоколом выполненных расчетов.

– Результаты исследования способов передачи параметров в подпрограммы.

– Выводы.

3.5 Контрольные вопросы

– Что такое процедура. Описание процедуры.

– Что такое функция. Описание функции.

– Варианты расположения подпрограмм и их особенности.

– Что такое область видимости имен и от чего зависит видимость имени.

– Способы передачи параметров в подпрограммы.

– Как создать и использовать дополнительный модуль.

– Написать подпрограмму по заданию преподавателя и рационально расположить ее в приложении.

Рекомендованая литература

1. Культин Н. Delphi 6. Программирование на Object Pascal. – СПб.:БХВ-Петербург,2002.

2. Ставровский А.Б. Турбо Pascal 7.0/ Учебник. – К.: BHV, 2000.

 

4 Лабораторная работа № 4.
Логический тип данных и разветвления в программах

Цели работы:

– Познакомиться с логическим типом данных.

– Познакомиться с логическими операциями.

– Научиться записывать и вычислять логические выражения.

– Познакомиться с инструкциями if … then … else и case … of.

– Ознакомиться с компонентами, которые обеспечивают возможность выбора вариантов.

– Создать приложение, реализующее разветвляющееся алгоритмы.

4.1 Краткие теоретические сведения

Логический тип данных

Тип Boolean используется для данных, которые могут принимать только два значения – истина и ложь. В языке Object Pascal этим значениям соответствуют константы True и False.

Данные такого типа обычно появляются как результат операций сравнения, и в некоторых других случаях. Например, результатом вычисления выражения 2<3 будет True, а результат вычисления выражения sin(x)>0 может быть и True и False, в зависимости от значения переменной х.

В таблице 4.1 приведены операции сравнения, определенные в языке Object Pascal.

Таблица 4.1 - Операции сравнения
Название операции сравнения	Запись на языке Object Pascal
Меньше	<
Меньше или равно	<=
Больше	>
Больше или равно	>=
Равно	=
Не равно	<>

4.1.1.1 Операции над логическими данными

Для данных типа Boolean определены три бинарных операции – «и», «или», «несовпадение». Последняя операция имеет и другие названий – «исключительно или», «сложение по модулю два». Результаты применения этих операций к возможным комбинациям логических операндов приведены в таблице 4.2. Эту таблицу следует знать, так же как и таблицу умножения.

Помимо бинарных, для данных типа Boolean определена одна унарная операция – «нет». В языке Object Pascal имя этой операции - not. Эта операция меняет значение логической переменной на противоположное. Например, результатом вычисления выражения not(2>3) будет True, а результат вычисления выражения not(sin(pi/2)<>0) будет False.

	Таблица 4.2 – Результаты выполнения логических операций
Первый операнд	Второй операнд	Логические операции
and (и)	or (или)	xor (несовпадение)
True	True	True	True	False
True	False	False	True	True
False	True	False	True	True
False	False	False	False	False

4.1.1.2 Логические выражения

Выражения, в которых используются операнды логического типа и операции над ними, называются логическими. Результатом вычисления такого выражения может быть только True или False. Частями логического выражения могут быть арифметические выражения, участвующие в операциях сравнения.

При записи логических выражений следует учитывать старшинство операций. Приоритеты операций, которые могут участвовать в логических выражениях, приведены в таблице 4.3.

Таблица 4.3 – Старшинство операций
Операции	Приоритет
@, not	Первый (самый высокий)
*, /, div, mod, and, shl, shr, as	Второй
+, –, or, xor	Третий
=, <>, <, >, <=, >=, in, is	Четвертый (самый низкий)

 

Так как операции сравнения имеют самый низкий приоритет, а вычислять их часто приходится в первую очередь, то, как правило, при записи логических выражений операции сравнения берутся в скобки.

Разветвляющиеся алгоритмы

В повседневной жизни мы часто сталкиваемся с такими видами алгоритмов. Например, если идет дождь, мы берем зонтик, а если мороз, надеваем теплую куртку. Разветвляющийся алгоритм предполагает, что некоторые действия могут выполняться только при определенных условиях.

При разработке разветвляющихся алгоритмов полезно изображать схемы алгоритмов, используя специальные обозначения. Схема алгоритма представляет собой как бы план написания программы. Составление таких схем не требует много времени, но существенно повышает производительность труда программиста. Некоторые условные обозначения, используемые при составлении схем алгоритмов, приведены в таблице 4.4.

При изображении алгоритма отдельные блоки нумеруются и соединяются линиями. Стрелки используются только для обратных направлений (снизу вверх и справа налево).

Таблица 4.4 - Условные обозначения для схем алгоритмов

	Начало и конец алгоритма
	Обработка информации, например, расчет по формуле
	Проверка условия и принятие решения. После этого блока возможны различные пути продолжения выполнения алгоритма
	Предопределенный процесс, например, обращение к процедуре.
	Вывод или ввод информации

 

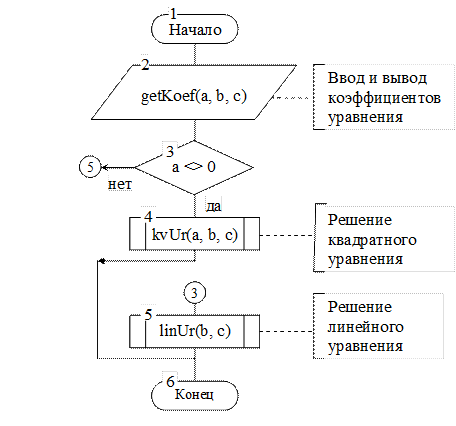
Рисунок 4.1- Схема алгоритма анализа коэффициентов квадратного уравнения

В качестве примера рассмотрим схемы алгоритма решения квадратного уравнения ax² + bx + c = 0. На рисунке 4.1 изображена укрупненная схема, в которой анализируется первый коэффициент уравнения и принимается решение, является ли уравнение квадратным, или оно линейное. В первом случае будет вызвана процедура решения квадратного уравнения, во втором – процедура решения линейного уравнения.

На рисунке 4.2 изображена схема алгоритма решения линейного уравнения. В этом алгоритме анализируются значения оставшихся коэффициентов. Если оба они равны нулю, то уравнению 0х + 0 = 0 удовлетворяет любое значение х. Если же b равно 0, а c не равно 0, то уравнение с = 0 решения не имеет. В остальных случаях корень уравнения определяется по формуле r = -c / b.

Рисунок 4.2 – Схема алгоритма решения линейного уравнения

Схему алгоритма решения квадратного уравнения, который должен выполняться, если коэффициент «а» не равен 0, следует составить самостоятельно и привести в отчете. Алгоритм должен предусматривать анализ дискриминанта и вывод значений действительных или комплексных корней.