Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные логические функции. Реализация основных логических функций на релейно-контактных схемах.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Далее приводятся основные положения двоичной алгебры. Отношения между двумя элементами здесь определяются отношением эквивалентности, обозначаемым знаком равенства, и тремя операциями: сложения (дизъюнкции), обозначаемой знаками <<+>> или <<V>>,умножения (конъюнкции) — <<•>> или<<^>> и отрицания (инверсии) — При выполнении всех трех операций отношения эквивалентности определяются следующими выражениями:
Эти постулаты позволяют обосновать законы двоичной алгебры. Законы одинарных элементов: универсального множества: х+ 1 = 1; х* 1 = х; нулевого множества: х= 0 = х; х • 0 = 0. Законы отрицания (теорема Моргана): двойного отрицания:
дополнительности: x + х • х = 0: двойственности:
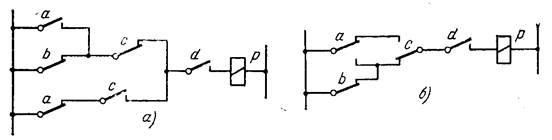
Законы поглощения (абсорбции): х1+х1х2=х1; х1(х1+х2)=х1; Законы склеивания: х1х2+х1 (х1+х2)(Х1+ Реализация основных логических функций на релейно-контактных схемах: Каждое устройство, состоящее из соединенных между собой катушек реле и контактов(контактов реле, кнопок, датчиков), можно описать с помощью булевых функций и, наоборот, любую логическую функцию можно реализовать с помощью схемы, состоящей из соединенных между собой катушек и контактов реле. Обычно при записи функций катушки реле обозначаются большими буквами, а контакты — маленькими. Включенное состояние реле (контакта реле) записывается как Р=1 (р=1), отключенное состояние реле (контакта реле)—Р=0 (р=0). Для простейшей схемы, изображенной на рис. 1,(а), можно записать: Р=1, если а1, и Р=0, если а=0, или Р—а. В схеме рис. 1,(б) реле Р включено, когда отключено реле А, или Р=а. На схеме рис. 1,(в) реле Р включено, если включены оба реле А и В: P=ab,(схема «и»)
Рис. 1. Реализация основных логических функций.
а на схеме 2-3,г реле Р включено, если включено хотя бы одно реле А или В: Р = а\/b,(схема «или») Отсюда вытекают общие правила: последовательному соединению контактов соответствует конъюнкция, параллельному — дизъюнкция, а нормально замкнутый контакт в схеме соответствует отрицанию. Следуя этим правилам, легко выразить функцию, реализованную схемой на рис. 2,(а):
Рис. 2. Схемы, реализующие функцию
77. Основные логические элементы и их функции. Функционально полный набор логических элементов.
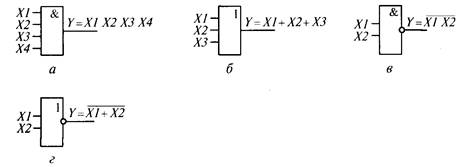
Логическими элементами называются микросхемы малой степени интеграции, реализующие простейшие логические функции двух — четырех аргументов. Наиболее распространены логические элементы, реализующие логические функции «И» (рис. 1, а), « ИЛИ» (рис. 1, б), « И-НЕ» (рис. 1, в) и «ИЛИ-НЕ» (рис. 1, г). К логическим элементам относятся также микросхемы, реализующие простейшие последовательностные алгоритмы (например, триггеры). Логические элементы «И» реализуют функцию логического умножения (конъюнкцию). Это означает, что выходной сигнал схемы «И» равен единице только в том случае, когда все ее входные сигналы равны единице. Логический элемент «И» называется также схемой совпадения. Логические элементы «ИЛИ» реализуют функцию логического сложения (дизъюнкцию), т.е. сигнал на выходе схемы «ИЛИ» равен нулю только тогда, когда все входные сигналы равны нулю. Логические элементы «И —НЕ» реализуют функцию инверсии логического произведения (функцию Шеффера), а элементы «ИЛИ —НЕ» — функцию инверсии логической суммы (функцию Пирса).
Рис. 1. Схемные обозначения логических элементов «И» (а), «ИЛИ» (б), «И-НЕ» (в), «ИЛИ-НЕ» (г). Таким образом, если логическое произведение равно единице, то элемент «И —НЕ» выдает нулевой сигнал на своем выходе; если логическая сумма равна единице, то элемент «ИЛИ —НЕ» также выдает нулевой сигнал. В противном случае на выходах элементов данного типа формируется единичный сигнал. В одном корпусе микросхемы обычно имеется четыре логических схемы — на два входа каждая, либо три схемы — на три входа каждая, либо две схемы — на четыре входа. С помощью элементов «И —НЕ» можно реализовать все базовые функции булевой алгебры, а следовательно, любые логические функции. Так же универсальны и элементы «ИЛИ —НЕ». Набор «И», «ИЛИ», «НЕ»- называют основным функционально полным. Эти наборы составляют основу микроэлектроники. Элементы других типов, которые при наличии элементов «И —НЕ» или «ИЛИ —НЕ» не являются обязательными для реализации алгоритмов управления, имеют, как правило, специальное назначение. Так, элементы «И» обычно являются усилительными элементами. Их допустимый выходной ток достигает 100 мА, в то время как обычные логические элементы имеют допустимый выходной ток до 5 мА.
Рис. 2. Реализация базовых логических функций на элементах И —НЕ: а — инверсия; б — логическое произведение; в — логическая сумма.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 939; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.72.210 (0.009 с.) |

 = х;
= х; = 1
= 1 =
= 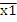 *
*  ;
; =
=  ;
;