
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общий вид экспериментальных переходных кривых теплоэнергетических процессов. Обобщенная энергетическая форма уравнений динамики регулируемых объектов.Содержание книги
Поиск на нашем сайте
Особенностью реального управления многими инерционными технологическими процессами, такими как процесс регулирования давления, расхода, уровня, температуры, является апериодичность переходных характеристик. Увеличение количества емкостей, составляющих регулируемый объект, приводит, очевидно, к соответствующему увеличению порядка дифференциального уравнения, описывающего процесс разгона для регулируемой величины в последней из емкостей при возмущении на входе в объект. Переходный процесс многоемкостного теплового регулируемого объекта за редким исключением описывается дифференциальными уравнениями, характеристические уравнения которых имеют лишь действительные корни. Поэтому процессы разгона в них протекают апериодически, а их кривые разгона являются суммами экспонент (рис. III. 8, кривые 2, 3, 4) и имеют характерную «S-образную» форму. Чем больше составляющих емкостей имеет регулируемый объект при прочих равных условиях, тем более полого идет кривая разгона в начале процесса и тем длительнее его течение (кривые 3 и 4 рис. III. 8). При отсутствии самовыравнивания в регулируемом объекте форма кривых разгона будет несколько иной (рис./III. 9). В этом случае любая из кривых будет уходить в бесконечность, становясь, при достаточном удалении от начала процесса, прямолинейной.
Рис. III. 8. Характеристики разгона многоемкостных объектов при наличии самовыравнивания. Цифры на рисунке соответствуют числу емкостей объекта
Общий вид экспериментальных переходных кривых таких процессов характеризуется тремя основамипараметрами: Т, г, V — постоянной времени, временем отставания и скоростью нарастания соответственно, а простейшей обобщенной моделью является модель -
Если к кривой разгона многоемкостного объекта (рис. III. 12) провести касательную в точке ее перегиба (или в бесконечности в случае отсутствия самовыравнивания рис. III. 13), то эта касательная отсечет на оси времени некоторый отрезок, обозначаемый те и называемый емкостным запаздыванием. Из кривых рис. III. 8, III. 9 легко видеть, что емкостное запаздывание при прочих равных условиях тем больше, чем большее число емкостей составляет регулируемый объект. Конечное отклонение регулируемой величины σ к определяется степенью самовыравнивания регулируемого объекта и равна ее обратной величине при единичном ступенчатом возмущении. Таким образом, течение процесса разгона многоемкостного регулируемого объекта, а, следовательно, и его кривая разгона приближенно характеризуются тремя величинами — скоростью разгона е, степенью самовыравнивания q и величиной времени емкостного запаздывания т е.
В очень большом числе случаев в тепловых регулируемых объектах имеет место так называемое чистое или транспортное запаздывание т0. Оно обусловливается тем, что с момента нанесения возмущения и до того момента, когда регулируемая величина начнет изменяться, должно пройти некоторое время, затрачиваемое на перемещение регулируемой среды от места нанесения возмущения до места измерения регулируемой величины. Таким образом, типовая характеристика разгона сложного (многоемкостного) теплового регулируемого объекта имеет характерный вид, изображенный на рис. III. 12 и III. 13. Сумма транспортного и емкостного запаздываний, т0 + те = т, называется полным или условным запаздыванием.
Рис. III. 12.. Кривая разгона сложного объекта с самовыравниванием и аппроксимация ее апериодическим звеном с транспортным запаздыванием т, равным сумме емкостного те и действительного транспортного т0 запаздываний.
(Обобщенная энергетическая форма уравнений динамики регулируемых объектов написана в вопросе 63, в конце)
При построении систем комплексной автоматизации, особенно систем, включающих цифровые управляющие машины, все больше выявляется недостаточность дифференциальных, разностных и интегральных уравнений как математического аппарата описания процессов управления. Обусловлено это большим количеством логических условий, встречающихся в подобных процессах управления, а также дискретностью многих действий. Необходим более общий способ описания процессов управления. Таким способом может служить алгоритм.
Термин алгоритм происходит от имени средневекового узбекского математика Аль-Хорезми, который еще в IX в. (825 г.) дал правила выполнения четырех арифметических действий в десятичной системе счисления. Процесс выполнения арифметических действий был назван алгоризмом. Алгоритм есть совокупность четко определенных правил, процедур или команд, обеспечивающих решение поставленной задачи за конечное число шагов. Под алгоритмом управления понимают совокупность правил приложения управляющих воздействий к исполнительным элементам объекта управления, обеспечивающих его функционирование с целью решения поставленной перед объектом задачи. Вырабатывает указанные воздействия управляющее устройство на основе уставок и ограничений, введенных оператором (априорная информация), и сигналов датчиков, вводимых обратными связями (текущая информация). Алгоритм — понятие весьма широкое; оно охватывает любую совокупность преобразований и логических условий, действующих в определенном порядке. Например, алгоритмом можно назвать любую инструкцию или предписание, определяющие порядок действия лица в конкретных условиях. Любая передаточная функция системы управления есть частный вид алгоритма. Способы записи алгоритмов Используются следующие способы записи алгоритмов:
|
||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.227.187 (0.01 с.) |

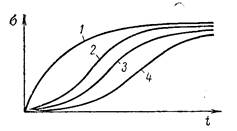
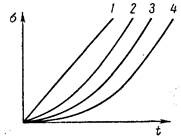 Рис. III. 9. Характеристики разгона многоемкостных объектов в отсутствии самовыравнивания. Цифры на рисунке соответствуют числу емкостей объекта
Рис. III. 9. Характеристики разгона многоемкостных объектов в отсутствии самовыравнивания. Цифры на рисунке соответствуют числу емкостей объекта





