
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Колебания и волны в упругих средахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МЕХАНИКА Поступательное движение Кинематика 1. Две материальные точки движутся по окружности радиусами R1 и R2, причем R2=2R1. При условии равенства линейных скоростей точек их центростремительные ускорения связаны соотношением
2. На рисунке представлен график зависимости пути S велосипедиста от времени t. Определите интервал времени после начала движения, когда велосипедист двигается со скоростью 2,5 м/с. 1) от 0 до 1 с 2) от 1 с до 3 с 3) от 3 с до 5 с 4) от 5 с до 7 с
1) 1. 2) 2. 3) 3. 4) во всех точках одинаково. 4. Камень, брошенный из окна второго этажа с высоты 4м, падает на землю на расстоянии 3м от стены дома. Модуль перемещения камня равен: 1)3м 2)4м 3)5м 4)7м
5. На рисунках изображены графики зависимости модуля ускорения от времени движения. Равномерному прямолинейному движению соответствует график 1) 1 2) 2 3) 3 4)4
1) А 2) Б 3) В 4) Г
7. Автомобиль движется по прямой улице. На графике представлена зависимость скорости автомобиля от времени. Модуль ускорения максимален в интервале времени 1) от 0 с до 10 с 2) от 10 с до 20 с 3) от 20 с до 30 с 4) от 30 с до 40 с 8. Мгновенную скорость тела при любом его движении определяет выражение а) 9. Уравнение зависимости скорости прямолинейно движущегося тела от времени имеет вид а) s = 2 t + 3 t 2 (м) б) s = 1,5 t 2 (м) в) s = 2 t + 1,5 t 2 (м) г) s = 3 t + t 2 (м) 10. Из перечисленных ниже величин векторными являются: а) путь б)только перемещение в) только скорость г) скорость и перемещение Динамика 1. Тело массой m=2 кг движется по плоскости таким образом, что зависимость его координат от времени имеет вид 1) 10 Н 2) 18 Н 3) 20 Н 4)24 Н
1) в точке 2 2) в точке 6 3) в точке 4 4) в точке 5 3. Тело массой 2 кг движется вдоль оси ОХ. Его координата меняется в соответствии с уравнением х=А+Вt+Ct2, где А=2м, В=3м/с, С=5м/с2. Импульс тела в момент времени t=2 c равен 1) 86 кг м/с 2) 48 кг м/с 3) 46 кг м/с 4) 26 кг м/с 4. Под действием равнодействующей силы, равной 5 Н, тело массой 10 кг движется 1) равномерно со скоростью 2 м/с 2) равномерно со скоростью 0,5 м/с 3) равноускоренно с ускорением 2 м/с2 4) равноускоренно с ускорением 0,5 м/с2 5. Парашютист спускается вертикально с постоянной скоростью 2 м/с. Систему отсчета, связанную с Землёй, считать инерциальной. В этом случае 1) вес парашютиста равен нулю 2) сила тяжести, действующая на парашютиста, равна 0 3) сумма всех сил, приложенных к парашютисту, равна 0 сумма всех сил, действующих на парашютиста, постоянна и не равна 0
7. При увеличении в три раза расстояния между центрами шарообразных тел сила гравитационного притяжения 1) увеличивается в 3 раза 2) уменьшается в 3 раза 3) увеличивается в 9 раз 4) уменьшается в 9 раз. 8. Закону сохранения импульса для случая взаимодействия двух тел соответствует выражение
1) 1 кг∙м/с 2) 4 кг∙м/с 3) 8 кг∙м/с 4) 16 кг∙м/с
10. Импульс силы в Международной системе единиц измеряется в 1) Н 2) кг 3) Н∙с 4) Дж Работа 1. Работа силы тяжести, совершаемая над искусственным спутником массой m, движущимся по круговой орбите радиусом R вокруг Земли со скоростью а) 2. Работа силы трения (коэффициент трения 0,3) при перемещении тела массой 2 кг на расстояние 10 м по горизонтальной поверхности под действием силы, параллельной этой поверхности равна а) 60 Дж б) 120 Дж в) -60 Дж г) -120 Дж 3. Груз поднимают вертикально на 3 м за 5с, прикладывая вертикальную силу 10 H. При этом совершают работу а) 6 Дж б) 30 Дж в) 50 Дж г) 150 Дж 4. Двигатель мощностью 3000 Вт работает в течение 5 мин. При этом он совершает работу а) 10 Дж б) 15 000 Дж в) 900 000 Дж г) 600 Дж 5. Работа диссипативных сил при перемещении тела из одной точки в другую: а) не зависит от траектории. б) зависит от траектории. в) равна 0. г) зависит от начального и конечного положения тела. 6. Работа консервативных сил зависит: а) от траектории движения б) от начального и конечного положения тела в) от формы тела г) от скорости движения тела 7. Сила тяжести, действующая на дождевую каплю массой 20 мг при ее падении с высоты 2 км, совершает работу а) 0,2 Дж б) 0 в) 0,4 Дж г) 0,04 Дж 8. Работа переменной силы на конечном перемещении равна а) 9. Единицы измерения работы в системе СИ а) Вт б) Дж в) Па г) Н
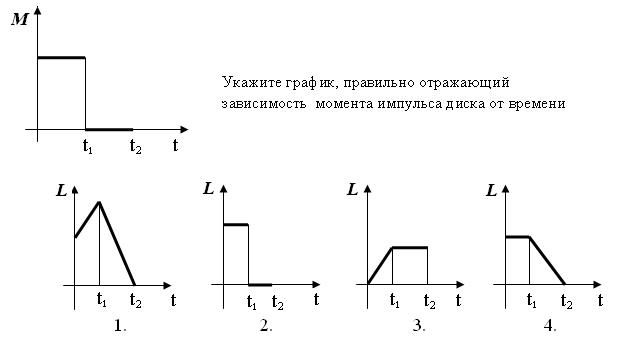
Вращательные движения Кинематика 1. При равномерном вращении угол поворота определяется формулой: a) 2. Модуль вектора угловой скорости определяется формулой а) 3. Единицы измерения угловой скорости в системе СИ а) 4. Частота вращения барабана 100 а)100 сек б)0,1 сек в)0.01 сек г)10 сек 5. Период обращения маховика 0,02 сек. Частота вращения его составляет а) 2 6. Связь между угловой и линейной скоростью определяется формулой а) 7. Модуль углового перемещения задан уравнением 1) 8 Вектор угловой скорости направлен: а) вдоль оси вращения б) перпендикулярно оси вращения в) вдоль вектора линейной скорости г) перпендикулярно вектору линейной скорости. 9. Векторными величинами являются 1) только угловая скорость 2) только угловое ускорение 3) только угловое перемещение 4) угловая скорость, угловое ускорение и угловое перемещение 10. Угол поворота при равнопеременном движении 1) Динамика 1. Момент инерции тела является: а) мерой инерции в поступательном движении б) мерой инерции во вращательном движении в) силовой характеристикой гравитационного поля г) количественной мерой взаимодействия тел 2. Момент инерции диска при увеличении его массы в 2 раза и при неизменных размерах 1) уменьшится в 2 раза 2) увеличится в 4 раза 3) уменьшится в 4 раза 4) увеличится в 2 раза 3. Момент инерции диска при неизменной массе и увеличении его диаметра в 3 раза 1) увеличится в 3 раза 2) уменьшится в 3 раза 3) увеличится в 9 раз 4) увеличится в 9 раз 4. Момент инерции тела при уменьшении его скорости вращения в 4 раза 1) уменьшится в 4 раза 2) увеличится в 4 раза 3) не изменится 4) уменьшится в 2 раза 5. Момент инерции стержня массой 400 г и длиной 60 см относительно оси, перпендикулярной стержню и проходящей через конец стержня, составляет а) г) 6. При перемещении оси вращения, перпендикулярной стержню, с конца стержня в его середину момент инерции стержня 1) увеличится в 4 раза 2) уменьшится в 4 раза * 3) не изменится 4) уменьшится в 2 раз 7. Кратчайшее расстояние от оси вращения до линии действия силы увеличивают в 2 раза, при этом момент силы 1) увеличится в 4 раза 2) уменьшится в 2 раза 3) увеличится в 2 раза 4) не изменится 8. Диск вращается равномерно с некоторой угловой скоростью W. Начиная с момента времени t = 0 на него действует момент сил, график временной зависимости которого представлен на рисунке.
9. Диск начинает вращаться под действием момента сил, график временной зависимости которого представлен на рисунке.
10. Момент импульса тела относительно неподвижной оси изменяется по закону L = a ∙ t. Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело:
Работа, энергия 1. Формула работы при вращении тела 1) 2. Вентилятор под действием сил торможения остановился, сделав 50 оборотов. Работа сил торможения 31,4 Дж. Момент сил торможения при этом 1) 10 Н∙м 2) 1 Н∙м 3) 0,1 Н∙м 4) 0 3. Момент сил торможения уменьшился в 3 раза, работа сил торможения при этом а) увеличилась в 3 раза б) уменьшилась в 3 раза в) не изменилась г) уменьшилась в 9 раз 4 При вращении тела угол поворота увеличили в 4 раза, при этом совершенная работа: а) уменьшилась в 2 раза б) увеличилась в 4 раза в) уменьшилась в 4 раза г) не изменилась 5. Кинетическая энергия вращения тела определяется формулой а) 6. При увеличении угловой скорости в 2 раза энергия вращения диска а) увеличится в 2 раза б) уменьшится в 2 раза в) увеличится в 4 раза г) не изменится 7. Диск и кольцо имеют одинаковую массу, радиус и угловую скорость. Соотношение между их кинетическими энергиями имеет вид а) 8. Обруч массой 2 кг катится со скоростью 6 а) 9. Обруч и диск имеют одинаковую массу и катятся с одинаковой скоростью. Их полные кинетические энергии соотносятся как а) Законы сохранения 1. Два шара, двигаясь навстречу друг другу по гладкой горизонтальной поверхности со скоростью 6 м/с каждый (относительно этой поверхности), после соударения стали двигаться вместе со скоростью 3 м/с. Отношение масс шаров равно 1) 1 2) 2 3) 3 4) 4 2. Для системы тел как при упругом, так и при неупругом ударах сохраняются неизменными следующие величины: 1) суммарная механическая энергия и импульс тел. 2) только суммарная механическая энергия тел. 3) только суммарный импульс тел. 4) только суммарная скорость шаров. 3. Два шара массами m и 2m движутся со скоростями, равными соответственно 2υ и υ. Первый шар движется за вторым и, догнав, прилипает к нему. Суммарный импульс шаров после удара равен 1) mυ 2) 2mυ 3) 3 mυ 4) 4 mυ 4. Шар и полая сфера, имеющие одинаковые массы и радиусы, скатываются без проскальзывания с горки высотой h. У основания горки: 1)скорости обоих тел будут одинаковы 2) больше будет скорость шара 3) больше будет скорость сферы 5. Потенциальная энергия взаимодействия с Землей гири массой 5кг увеличилась на 75 Дж. Это произошло в результате того, что гирю 1) подняли на 1,5м 2) опустили на 1,5м 3) подняли на 7м 4) опустили на 7м 6. Груз массой 1кг под действием силы 50 Н, направленной вертикально вверх, поднимается на высоту 3м. Изменение кинетической энергии груза при этом равно 1) 30 Дж 2) 120 Дж 3) 150 Дж 4) 180 Дж 7. Спортсмен-фигурист сообщает себе медленное вращение вокруг вертикальной оси. Резко сгруппировавшись, он уменьшает момент инерции своего тела в 1,2 раза. При этом момент импульса L и кинетическая энергия E к спортсмена: а) L и E к – не изменяются. б) L – не изменяется, E к – увеличилась в 1,2 раза. в) L – не изменяется, E к – увеличилась в 1,44 раза. г) E к – не изменяется, L – увеличилась в 1,2 раза. 8. Шар и полая сфера, имеющие одинаковые массы и радиусы, скатываются без проскальзывания с горки высотой h. К основанию горки: А) быстрее скатится шар; Б) быстрее скатится полая сфера; В) оба тела скатятся одновременно. 9 Шар и полая сфера, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания на горку. Если начальные скорости этих тел одинаковы, то: А) оба тела поднимутся на одну и ту же высоту; Б) выше поднимется полая сфера; В) выше поднимется шар.
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ 1. Материальная точка на пружине массой 1. 100 2. Материальная точка массой 1. 25 с-1. 2. 15 с-1 . 3. 5 с-1. 3. Материальная точка массой 1. 12,56 с, 2. 6,28 с, 3. 3,14 с. 4. Полная энергия материальной точки массой m, колеблющейся по закону 1. 5. Дифференциальное уравнение гармонических колебаний пружинного маятника 1. 2. 3. 6. Какое из приведенных уравнений описывает гармонические колебания с частотой 0,5 Гц и амплитудой 0,6 м? Начальная фаза колебаний равна нулю. 1. x = 0,6 cos π t.2. x = 0,6 cos 0,5 t. 3. x = 1,2 sin π t. 7. Как изменится период колебаний груза на пружине, если массу груза увеличить в 4 раза? 1. Увеличится в 4 раза. 2. Увеличится в 2 раза. 3. Уменьшится в 2 раза. 8. Циклическая частота гармонических колебаний, показанных на рисунке, равна:
1. 9. Материальная точка совершает колебания по закону: 1. 10. На рисунке показанграфик гармонического колебания.
Этому графику соответствует уравнение: 1.
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ 1. Дифференциальное уравнение вынужденных колебаний имеет вид:
1. 3. 2. Какое дифференциальное уравнение соответствуетвынужденным колебаниям: 1. 3. 3. Циклическая частота в установившихся вынужденных колебаниях определяется: 1. собственной циклической частотой колебательной системы ωо (β=0). 2. циклической частотой вынуждающей силы ωв. 3. условной циклической частотой затухающих колебаний ω (β≠0). 5.
1. 2. 3. 5. Резонансная циклическая частота определяется по формуле: 1. 6. Амплитуда вынужденных колебаний в колебательной системе, в которой коэффициент затухания не равен нулю (β≠0), принимает максимальное значение при условии: 1. 7. Амплитуда вынужденных колебаний в колебательной системе, в которой коэффициент затухания равен нулю (β=0), принимает максимальное значение при условии: 1. 8. В колебательной системе, совершающей вынужденные колебания, коэффициент затухания равен нулю (β=0). Когда циклическая частота вынуждающей силы 1. 9. В колебательной системе, совершающей вынужденные колебания, коэффициент затухания не равен нулю (β≠0). Когда циклическая частота вынуждающей силы 1. 10. В реальной колебательной системе резонанснаступает в том случае, если циклическая частота вынуждающей силы ωв.: 1. ВОЛНЫ В УПРУГИХ СРЕДАХ 1. Механические волны не могут распространяться: 1. в твердых телах. 2. в жидкостях. 3. в вакууме. 2. Поперечные механические волны могут распространяться:
3. Уравнение плоской синусоидальной волны имеет вид: 1. 2. 3. 4. Если числовое значение волнового вектора k = 2,512·10-4 м-1, то длина волны, распространяемой в упругой средеравна: 1. 5,5 м. 2. 2,5 м. 3. 1,5 м. 5. Две синусоидальные волны когерентны, если: 1. они распространяются в упругой среде в одном направлении. 2. их частоты одинаковы и разность фаз не зависит от времени. 3. их частоты одинаковы и разность фаз зависит от времени. 6. Интерференция двух когерентных волн – это явление, состоящее в устойчивом во времени их взаимном усилении в одних точках пространства и ослаблении в других точках пространства, в зависимости: 1. от соотношения между фазами этих волн, 2. от соотношения между амплитудами этих волн, 3. от направления распространения этих волн. 7. Интерференционные максимумы будут получаться в точках пространства, в которых геометрическая разность хода волн 1. четному числу полуволн 2. нечетному числу полуволн 3. 0. 8. Интерференционные минимумы будут получаться в точках пространства, в которых геометрическая разность хода волн 1. четному числу полуволн 2. нечетному числу полуволн 3. 0.
9. Уравнение стоячей волны имеет вид: 1. 2. 3. 10. Длина волны 1. одному периоду Т. 2. одному полупериоду 3. одной четвертой части периода
Первый закон термодинамики
1.
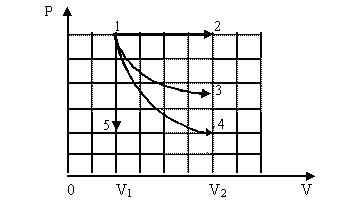
На р-V диаграмме показаны 5 процессов, происходящих с газом, при этом исходное состояние газа для всех процессов было одинаковое. Укажите, при каких процессах внутренняя энергия газа убывала. 1. 1→2, 1→3; 2. 1→2, 1→4; 3. 1→3, 1→4; 4. 1→5. 2. На р-V диаграмме показаны 5 процессов, происходящих с газом, при этом исходное состояние газа для всех процессов было одинаковое. Укажите в каком из процессов совершенная газом работа максимальна.
1. 1→2. 2. 1→3. 3. 1→4. 4. 1→5. 3. Одноатомный идеальный газ занимал объем V0. После подвода к нему при изобарном процессе количества теплоты Q объем газа увеличился в 2 раза. Подведенное к газу количество теплоты равно: 1. 4. В ходе некоторого процесса давление и объем идеального одноатомного газа изменялись так, что Р V 4 = const. При неизменной массе газа и увеличении его объема в 2 раза внутренняя энергия газа уменьшится в: 1. 5. Одноатомный идеальный газ изохорно нагревается. Укажите неверное утверждение: 1. 6. Идеальный газ переходит из состояния 1 через состояние 2 в состояние 3, как показано на р-V диаграмме. Совершенная газом работа равна:
1. 4 P0V0. 2. 2 P0V0. 3. 2,5 P0V0. 4. 3 P0V0. 7. В ходе некоторого процесса давление и объем газа изменяются таким образом, чтo PV3=const. Во сколько раз увеличится внутренняя энергия идеального одноатомного газа при уменьшении его объема в 2 раза? 1. не изменится. 2. в 1,41 раза. 3. в 2 раза. 4. в 4 раза. 8. На диаграмме Т→V показан процесс изменения состояния идеального газа. Газ совершает работу 3 кДж. Начальное давление 106Па. Количество теплоты, полученное газом равно:
1. 1кДж. 2. 3кДж. 3. 4 кДж. 4. 7 кДж. 9. На рисунке представлен график зависимости давления одноатомного идеального газа от его объема. Газ получил количество теплоты 500 кДж. Внутренняя энергия газа при этом:
1. не изменилась. 2. увеличилась на 100 кДж. 3. уменьшилась на 100 кДж. 4. увеличилась на 300 кДж.
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ Электростатика 1. В углах квадрата находятся заряды (+ q), (+ q), (– q), (– q), как показано на рисунке. На положительный точечный заряд, помещенный в центр этого квадрата, будет действовать кулоновская сила, направленная:
1. вниз 2. вверх 3. влево 4. вправо 2. Электрическое поле создается двумя точечными зарядами +q и -q, как показано на рисунке. Вектор напряженности электрического поля, создаваемого этими зарядами, в точке А имеет направление:
1. 2. 3. 4. 5. напряженность поля в точке А равна нулю. 3. Работа сил поля при перемещении электрического заряда 1 мКл между точками А и В в однородном электрическом поле с напряженностью 100 В/м равна: 1. 4. Конденсатор емкостью 1. увеличится в 2 раза. 2. уменьшится в 2 раза. 3. не изменится. 4. увеличится в 5. Величины двух точечных зарядов, взаимодействующих друг с другом, увеличили в два раза, а расстояние между ними уменьшили в два раза. Модуль силы взаимодействия между этими зарядами: 1. увеличился в два раза. 2. уменьшился в два раза. 3. не изменился. 4. увеличился в 1,4 раза. 5. уменьшился в 8 раз. 6. Модуль силы взаимодействия между двумя точечными заряженными телами равен F. Если заряд одного тела увеличить в 4 раза, а второго уменьшить в 2 раза, то модуль силы взаимодействия между этими телами станет равным: 1. F 2. 2F 3. F/2 4. 8F 7. Напряженность электростатического поля, созданного точечным зарядом, при увеличении расстояния от него в два раза: 1. уменьшится в два раза 2. увеличится в два раза 3. уменьшится в четыре раза 4. уменьшится в восемь раз 8. На рисунке показано распределение электрических зарядов в пространстве. Согласно теореме Остроградского – Гаусса поток вектора напряженности электростатического поля через замкнутую поверхность S3 (или S1, или S2) равен:
1. 0 2. 9. Электростатическое поле создается заряженной сферой, радиус которой R, а заряд +q. В точке А напряженность электрического поля и градиент потенциала имеют, соответственно, направления: 10. Электростатическое поле создается заряженной сферой, радиус которой R, а заряд -q. В точке А напряженность электрического поля и градиент потенциала имеют, соответственно, направления: Электрический ток 1. Если однородный проводник разрезать на две равные части и соединить эти части параллельно, то его сопротивление: 1) не изменится. 2) уменьшится в 2 раза. 3) уменьшится в 4 раза. 4) правильный ответ не приведен. 2. 1) 4) 3. 1) 1 2) 2 3) 3 4) 4 5) на всех одинаковое. 4. Если увеличить в 2 раза напряжение на концах проводника, а его длину уменьшить в 2 раза, то сила тока, протекающего через проводник: 1. Не изменится. 2. Увеличится в 2 раза. 3. Увеличится в 4 раза. 4. Правильный ответ не приведен. 5. В цепь источника тока с ЭДС 12 В и внутренним сопротивлением 2 Ом включили резистор с сопротивлением 4 Ом. Сила тока в цепи равна: 1. 2А 2. 3А 3. 6А 4. 24А 6.
1. 14 Ом 2. 8 Ом 3. 7 Ом 4. 10 Ом 7.
1. 5 Ом 2. 6 Ом 3. 15 Ом 4. 25 Ом 8.
9. К источнику тока с ЭДС = 6 В подключили реостат. На рисунке показан график изменения силы тока в реостате в зависимости от его сопротивления. Внутреннее сопротивление источника тока равно:
1. 0,5 Ом 2. 1 Ом 3. 2 Ом 4. 6 Ом
10. На рисунке показана зависимость силы тока в электрической цепи от времени.
Заряд, прошедший по проводнику на интервале времени от 5 до 15 с (в мКл) равен: 1. 250 2. 200 3. 300 4. 450 11. На рисунке показана зависимость силы тока в электрической цепи от времени.
Заряд, прошедший по проводнику на интервале времени от 10 до 20 с (в мКл) равен: 1. 350 2. 200 3. 100 4. 150 12. Зависимость удельного сопротивления металлического проводника от температуры соответствует графику… 13. Зависимость удельного сопротивления проводника от температуры в области сверхпроводящего перехода представлена графиком
14. Отношение удельных сопротивлений этих
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 1493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.249.84 (0.016 с.) |

 1) а1=2а2 2) а1=а2 3) а1=1/2а2 4) а1=4а2
1) а1=2а2 2) а1=а2 3) а1=1/2а2 4) а1=4а2 3. Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рисунке. Центростремительное ускорение максимально в точке
3. Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рисунке. Центростремительное ускорение максимально в точке
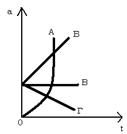 6. Равноускоренному движению соответствует график зависимости модуля ускорения от времени, обозначенный на рисунке буквой
6. Равноускоренному движению соответствует график зависимости модуля ускорения от времени, обозначенный на рисунке буквой
 б)
б)  в
в  г)
г) 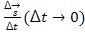
 Соответствующее уравнение для пройденного телом пути
Соответствующее уравнение для пройденного телом пути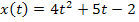 ,
,  . При этом модуль равнодействующей силы равен
. При этом модуль равнодействующей силы равен 2. На рисунке изображён тонкий невесомый стержень, к которому в точках 1 и 3 приложены силы F1=100 H и F2=300 H. Стержень будет в равновесии, если ось вращения расположить
2. На рисунке изображён тонкий невесомый стержень, к которому в точках 1 и 3 приложены силы F1=100 H и F2=300 H. Стержень будет в равновесии, если ось вращения расположить
 9. На рисунке представлен график зависимости модуля силы F, действующей на тело, от времени. Изменение импульса тела за 4 с равно
9. На рисунке представлен график зависимости модуля силы F, действующей на тело, от времени. Изменение импульса тела за 4 с равно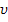 , за один полный оборот равна
, за один полный оборот равна б)
б) 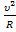 в)
в)  г) 0
г) 0 б)
б)  в)
в)  г)
г) 
 б)
б)  в)
в)  г)
г) 
 в)
в)  г)
г) 
 б)
б)  в)
в)  г)
г) 
 . Период обращения барабана:
. Период обращения барабана: б) 50
б) 50  б)
б)  * г)
* г)  Угловая скорость определяется как
Угловая скорость определяется как 2)
2)  3)
3)  4)
4) 
 3)
3) 

 б)
б)  в)
в) 



 2)
2)  3)
3)  4)
4) 
 б)
б)  в)
в)  * г)
* г) 
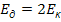 б)
б)  в)
в)  г)
г) 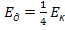
 б)
б) 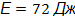 в)
в)  г)
г) 
 б)
б)  в)
в)  г)
г) 
 = 3 кг совершает гармонические колебания по закону:
= 3 кг совершает гармонические колебания по закону:  . Жесткость пружины равна:
. Жесткость пружины равна: . 2. 75
. 2. 75  совершает гармонические колебания. Циклическая частота колебаний
совершает гармонические колебания. Циклическая частота колебаний  равна:
равна: совершает гармонические колебания по закону
совершает гармонические колебания по закону  . Период колебаний
. Период колебаний  равен:
равен: , определяется по формуле:
, определяется по формуле: . 2.
. 2.  . 3.
. 3.  .
. 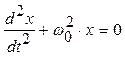 . Решение этого уравнения имеет вид:
. Решение этого уравнения имеет вид: .
. .
. .
.
 . 2.
. 2.  . 3.
. 3.  .
. . 2.
. 2.  . 3.
. 3.  .
. 2.
2. 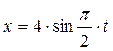 3.
3. 
 . Решением этого уравнения является:
. Решением этого уравнения является: . 2.
. 2.  .
. .
. . 2.
. 2.  .
. .
.
 . 2.
. 2.  . 3.
. 3.  .
. . 2.
. 2.  . 3.
. 3.  .
. стремится к собственной циклической частоте
стремится к собственной циклической частоте  (
( ) амплитуда вынужденных колебаний
) амплитуда вынужденных колебаний  стремится:
стремится: . 2.
. 2.  . 3.
. 3. 
 стремится к резонансной циклической частоте
стремится к резонансной циклической частоте  (
(  ) амплитуда вынужденных колебаний
) амплитуда вынужденных колебаний  стремится:
стремится: , 2.
, 2.  . 2.
. 2.  . 3.
. 3.  .
.


 равна:
равна: .
. .
. равна:
равна: - это расстояние, на которое распространяется волновой процесс за время равное:
- это расстояние, на которое распространяется волновой процесс за время равное: .
. .
.
 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  .
. . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  .
.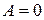 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  .
.






 ; 2)
; 2)  ; 3.
; 3. 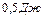 ; 4.
; 4.  ; 5)
; 5)  .
. подключен к источнику напряжения. Затем последовательно с данным конденсатором подключили другой конденсатор такой же емкости
подключен к источнику напряжения. Затем последовательно с данным конденсатором подключили другой конденсатор такой же емкости 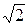 . 5. уменьшится в
. 5. уменьшится в 
 3.
3.  4.
4. 


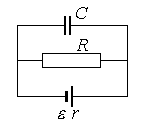 В изображенной на схеме цепи, состоящей из источника тока с ЭДС
В изображенной на схеме цепи, состоящей из источника тока с ЭДС  и внутренним сопротивлением
и внутренним сопротивлением 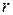 , внешнего сопротивления
, внешнего сопротивления  и конденсатора
и конденсатора  ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  .
.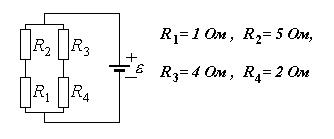 На рисунке приведена электрическая схема и указаны величины сопротивлений. За единицу времени наибольшее количество теплоты выделится на сопротивлении, номер которого:
На рисунке приведена электрическая схема и указаны величины сопротивлений. За единицу времени наибольшее количество теплоты выделится на сопротивлении, номер которого: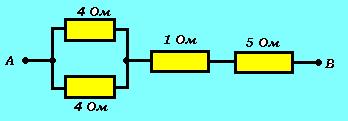 Сопротивление между точками А и В участка электрической цепи, представленной на рисунке, равно:
Сопротивление между точками А и В участка электрической цепи, представленной на рисунке, равно: Четыре резистора соединены по схеме, изображенной на рисунке. Общее сопротивление цепи между точками А и В равно:
Четыре резистора соединены по схеме, изображенной на рисунке. Общее сопротивление цепи между точками А и В равно: По участку цепи АВ, показанному на рисунке, течет постоянный ток I = 3 A. Считая, что сопротивление амперметра равно нулю, его показание будет:
По участку цепи АВ, показанному на рисунке, течет постоянный ток I = 3 A. Считая, что сопротивление амперметра равно нулю, его показание будет: 1. 1 А 2. 2 А 3. 1,5 А 4. 0,5 А 5. 1,33 А
1. 1 А 2. 2 А 3. 1,5 А 4. 0,5 А 5. 1,33 А


 На рисунке представлена зависимость плотности тока j, протекающего в проводниках 1 и 2, от напряженности электрического поля Е.
На рисунке представлена зависимость плотности тока j, протекающего в проводниках 1 и 2, от напряженности электрического поля Е.


