Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гармонические колебания. Вынужденные и затухающие колебания.Содержание книги
Поиск на нашем сайте
Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму. Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии. Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом: Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени. Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида Волны. Уравнение волны. Волна — изменение состояния среды (возмущение), распространяющееся в этой среде и переносящее с собой энергию. Другими словами: «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины, например, плотности вещества, напряжённости электрического поля, температуры». Перенос энергии — принципиальное отличие волн от колебаний, в которых происходят лишь «местные» преобразования энергии. Волны же, как правило, способны удаляться на значительные расстояния от места своего возникновения (по этой причине волны иногда называют «колебанием, оторвавшимся от излучателя»). Математическое описание волн основывается на представлении о них, как о пространственно распространяющихся колебаниях, и в общем виде записывается:
где u — отклонение от некоего среднего положения в точке r во время t. Более определённый вид уравнения зависит от типа волны. Гармоническая волна Изменение колеблющейся величины u для гармонически распространяющейся волны в начале координат описывается формулой:
где A — амплитуда, t — время, а T — период волны. В любой другой точке, расположенной на расстоянии r от начала координат в направлении распространения волны, изменение u происходит с опозданием на время t 1:
Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t. Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом. Уравнение плоской волны Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер. Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t:
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости
– это уравнение плоской волны. Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так:
Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны. Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид:
Уравнение волны можно записать и в другом виде. Введем волновое число
где Так как
Уравнение сферической волны В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической. Предположим, что фаза колебаний источника равна w t (т.е.
где А равна амплитуде на расстоянии от источника равном единице. Уравнение (5.2.7) неприменимо для малых r, т.к. при Бегущими волнами называются волны, которые переносят в пространстве энергию. Перенос энергии в волнах количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова (по имени русского ученого Н. А. Умова (1846— 1915), решившего задачу о движении энергии в среде). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны. Для вывода уравнения бегущей волны — зависимости смещения колеблющейся частицы от координат и времени — рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распространения волны (рис. 220). В данном случае волновые поверхности перпендикулярны оси х, а так как все точки волновой поверхности колеблются одинаково, то смещение x будет зависеть только от х и t, т. е. x=x (х, t). На рис. 220 рассмотрим некоторую частицу среды В, находящуюся от источника колебаний О на расстоянии х. Если колебания точек, лежащих в плоскости х= 0, описываются функцией x(0, t)=А coswt, то частица среды В колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на т, так как для прохождения волной расстояния х требуется время t= x/v, где v — скорость распространения волны. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид x(x,t)=Acosw(t-x/v), (154.1) откуда следует, что x (х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то x(х, t)=A cosw(t+x/v). В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид x(x,t)=Acos[w(t -х/v)+j0], (154.2) где А= const — амплитуда волны, w — циклическая частота волны, j0 — начальная фаза колебаний, определяемая в общем случае выбором начал отсчета х и t, [w (t-x /v)+j0]— фаза плоской волны. Для характеристики волн используется волновое число k=2p/l=2p/vT=w/v. (154.3) Учитывая (154.3), уравнению (154.2) можно придать вид x(x,t)=A cos(wt-kх+j0). (154.4) Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (154.4) только знаком члена kx. Основываясь на формуле Эйлера (140.7), уравнение плоской волны можно записать в виде x(x,t)=Aei(wt-kx+j0), где физический смысл имеет лишь действительная часть. Предположим, что при волновом процессе фаза постоянна, т. е. w(t-x/v)+j0=const. (154.5) Продифференцировав выражение (154.5) и сократив на w, получим dt -(1/v) dx=0, откуда dx/dt=v. Следовательно, скорость v распространения волны в уравнении есть не что иное, как скорость перемещения фазы волны, и ее называют фазовой скоростью. Повторяя ход рассуждений для плоской волны, можно доказать, что уравнение сферической волны — волны, волновые поверхности которой имеют вид концентрических сфер, записывается как x(r,t)=A0/rcos(wt-kr+j0), (154.7) где r — расстояние от центра волны до рассматриваемой точки среды. В случае сферической волны даже в среде, не поглощающей энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием по закону 1 /r. Уравнение (154.7) справедливо лишь для r, значительно превышающих размеры источника (тогда источник колебаний можно считать точечным). Из выражения (154.3) вытекает, что фазовая скорость v=w/k. (154.8) Если фазовая скорость волн в среде зависит от их частоты, то это явление называют дисперсией волн, а среда, в которой наблюдается дисперсия волн, называется диспергирующей средой. Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением — дифференциальным уравнением в частных производных
где v — фазовая скорость, D= д 2/ д x2 + д 2/ д y2 + д 2/ д z2 — оператор Лапласа. Решением уравнения (154.9) является уравнение любой волны. Соответствующей подстановкой можно убедиться, что уравнению (154.9) удовлетворяют, в частности, плоская волна (см. (154.2)) и сферическая волна (см. (154.7)). Для плоской волны, распространяющейся вдоль оси х, волновое уравнение имеет вид
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1842; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.63.107 (0.008 с.) |

 , где х — значение изменяющейся величины, t — время, А — амплитуда колебаний, ω — циклическая частота колебаний,
, где х — значение изменяющейся величины, t — время, А — амплитуда колебаний, ω — циклическая частота колебаний, 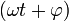 — полная фаза колебаний,
— полная фаза колебаний,  — начальная фаза колебаний.
— начальная фаза колебаний. в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний
в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний  или её квадрата.
или её квадрата.
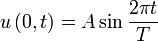 или
или 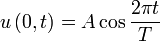
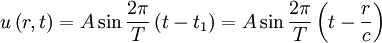 где c — скорость распространения волны в данной среде.
где c — скорость распространения волны в данной среде.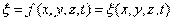
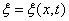 . Пусть колебание точек, лежащих в плоскости
. Пусть колебание точек, лежащих в плоскости 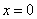 , имеет вид (при начальной фазе
, имеет вид (при начальной фазе 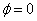 )
)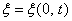
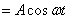
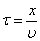 .
.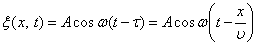 ,
,
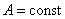 . Это будет, если энергия волны не поглощается средой.
. Это будет, если энергия волны не поглощается средой. , или
, или 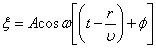 .
.
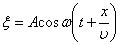 .
.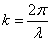 , или в векторной форме:
, или в векторной форме: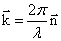 ,
,
 – волновой вектор,
– волновой вектор, 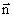 – нормаль к волновой поверхности.
– нормаль к волновой поверхности.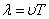 , то
, то 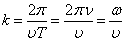 . Отсюда
. Отсюда 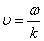 . Тогда уравнение плоской волны запишется так:
. Тогда уравнение плоской волны запишется так: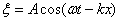 .
.
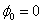 ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу
). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу 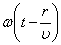 . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону
. Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону 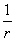 . Следовательно, уравнение сферической волны:
. Следовательно, уравнение сферической волны: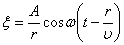 , или
, или 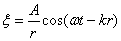 ,
,
 , амплитуда стремится к бесконечности. То, что амплитуда колебаний
, амплитуда стремится к бесконечности. То, что амплитуда колебаний 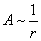 , следует из рассмотрения энергии, переносимой волной.
, следует из рассмотрения энергии, переносимой волной.