
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрическое сопротивление металлов. Сверхпроводимость.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Электрическое сопротивление металлов. Квантовая теория электропроводности металлов сводится к следующему: а. В случае идеальной кристаллической решетки электроны проводимости при своем движении не должны испытывать никакого сопротивления. Сопротивление возникает тогда, когда в решетке появляются дефекты структуры, то есть, нарушается периодичность решетки. б. В реальных кристаллах есть два механизма нарушения структуры: примесный и тепловой. Соответственно различают примесное удельное сопротивление rn и тепловое (колебательное) rТ. Согласно правилу аддитивности сопротивлений полное сопротивление металла r равно их сумме, r=rn+rТ. (13.1) в. Примесное сопротивление rn обусловлено наличием инородных атомов в решетке (атомов примеси). Если металл достаточно чистый и концентрация атомов примеси невелика, то примесное сопротивление при обычной температуре также относительно невелико. Оно практически не зависит от температуры и становиться заметным лишь вблизи абсолютного нуля. Благодаря примеси удельное сопротивление металла не должно обращаться в нуль даже при Т =0К. г. Тепловое сопротивление rТ возникает благодаря рассеянию электронов проводимости на флуктуациях плотности узлов кристаллической решетки, возникающих при тепловом колебательном движении узлов. В квантовой теории тепловое колебательное движение атомов решетки трактуется как система стоячих звуковых волн в кристалле - фононов. Поэтому говорят о рассеянии электронов проводимости на фононах. В отличие от классической теории электропроводности металлов Друде - Лоренца, прогнозирующей зависимость сопротивления от температуры вида r ~ r = r 0 aТ, что соответствует эмпирической формуле r = r 0 (1+ a t). В квантовой теории получается, что при Т ®0 полное удельное сопротивление металла r должно стремиться к примесному rn. На рис.90 показана опытная зависимость удельного сопротивления чистого натрия от температуры. При Т ®0К r ® rn =4·10-11Ом·м, что составляет примерно 0,4% от сопротивления при Т =273К. Уже при температурах Т ³ 20К зависимость r (Т) становится практически линейной. д. Электрический ток толкуется в квантовой теории как дрейф электронов в периодическом поле кристалла. Этот дрейф происходит под действием постоянной электрической силы еЕ, где Е - напряженность электрического поля, создающего ток. Оказалось, что скорость дрейфа электронов зависит от глубины их положения в зоне проводимости. Эта зависимость выражается через эффективную массу mэф электрона. В отличие от массы покоя mе свободного электрона эффективная масса электрона в зоне проводимости металла – величина переменная, зависящая от ширины зоны. Вблизи дна зоны эффективная масса электронов положительна. Направление дрейфа соответствует вектору плотности тока. По мере подъема к верхней границе зоны эффективная масса принимает бесконечно большое значение mэф =¥, а затем становится отрицательной. Соответственно и скорость дрейфа электронов, имея правильное направление у дна зоны, постепенно проходит через нуль и принимает отрицательные (“неправильное”) значения у верхней границы зоны. Соотношения, полученные в приближении свободных электронов в теории Друде – Лоренца, оказываются справедливыми для электронов, движущихся в периодическом поле решетки, если в них заменить массу покоя электрона mе на эффективную mэф. 2. Сверхпроводимость. В 1911 году Камерлинг – Оннес, измеряя сопротивление ртути в области низких температур, обнаружил, что при Т =4,2К сопротивление ртути практически падало до нуля. Это явление стали называть сверхпроводимостью. На рис. 91 показаны опытные кривые зависимости удельного сопротивления некоторых чистых металлов от температуры вблизи абсолютного нуля. Очевидно, что явление не сводится к нормальному падению удельного сопротивления бездефектного кристалла, когда rn =0, и rТ В таблице 13.1 приведены значения Ткр для некоторых чистых элементов и химических соединений, изученных раньше других. Сейчас известно около 30 сверхпроводящих химических элементов и свыше 500 сверхпроводящих материалов. Эффекты сверхпроводимости. а. Электрический ток, возбужденный в сверхпроводящем кольце, может циркулировать в нем годами. б. Эффект Мейснера. В 1933 году Вольтер Мейсснер и Р. Оксенфельд обнаружили, что вещество, помещенное в магнитное поле (рис. 92 слева), при переходе в сверхпроводящее состояние не замораживает находящееся в нем магнитное поле, как это должно было быть при простом переходе вещества в состояние с нулевым сопротивлением, а выталкивает его из своего объема. Это присуще идеальным диамагнетикам с нулевой магнитной проницаемостью m =0. Вещество в сверхпроводящем состоянии приобретает два не связанные друг с другом фундаментальные свойства: идеальную проводимость и идеальный диамагнетизм. Эффект Мейснера позволяет устойчиво подвешивать сверхпроводящие тела в магнитном поле (рис.93). Из того, что магнитное поле не проникает в сверхпроводник, следует, что электрический ток может течь лишь по поверхности сверхпроводника. Ведь если бы ток мог протекать в толще сверхпроводника, то вокруг него в толще сверхпроводника было бы магнитное поле. И действительно, опыт показывает, что электрический ток течет в сверхпроводнике в поверхностном слое толщиной l =10¸100нм. На эту глубину в сверхпроводник проникает и магнитное поле, убывая с расстоянием x от поверхности по экспоненциальному закону В=В 0 exp(- x/l), (13.2) где В 0 – индукция на поверхности. в. Эффект критического магнитного поля. Он состоит в том, что при достижении магнитным полем, в котором находится сверхпроводник, некоторого предельного значения индукции Вкр »10-2¸101Тл, сверхпроводимость исчезает. На рис.94 показана зависимость Вкр от температуры для свинца (верхняя кривая) и для олова (нижняя кривая). При критической температуре Т=Ткр критическое поле равно нулю, Вкр =0, а с понижением температуры Вкр увеличивается. Если усиливать ток, идущий по сверхпроводнику, то при некотором его критическом значении Iкр сверхпроводящее состояние разрушается. Поскольку магнитное поле В пропорционально току I, то зависимость Iкр от температуры аналогична зависимости Вкр (Т). Эффект критического магнитного поля усложняет технику получения сверхсильных магнитных полей с помощью сверхпроводящих контуров. Расчет критического тока должен учитывать, что ток течет в приповерхностном слое. Например, у проводника диаметром 1мм при l= 35нм сечение приповерхностного слоя, по которому течет ток, около 10-4мм2. Это составляет около 0,01% всего сечения проводника. г. Эффект Джозефсона. В 1962 году Брайан Джозефсон теоретически предсказал два эффекта, суть которых в следующем. Подсоединим к сверхпроводнику (на рис.95а он изображен в виде бруска) амперметр А с источником постоянного тока e и вольтметр V. При замыкании ключа Кл в цепи возникает постоянный ток, регистрируемый амперметром. Так как сопротивление сверхпроводника равно нулю, то вольтметр показывает нуль. Разрежем сверхпроводник на две части и раздвинем их так, чтобы между ними возник диэлектрический зазор толщиной d»1нм. Как предсказал Джозефсон, при включении такого сверхпроводника в цепь может наблюдаться один из следующих двух эффектов. Стационарный эффект Джозефсона. Через сверхпроводник по-прежнему протекает постоянный ток. Оказывается, ток может течь без сопротивления не только через сверхпроводник, но и через щель в нем, если она достаточно узка (рис.95б). Нестационарный эффект Джозефсона. На концах сверхпроводника со щелью может возникнуть постоянная разность потенциалов. В этом случае из щели излучается высокочастотная электромагнитная волна (рис.95в). Через сверхпроводник течет не только постоянный, но и высокочастотный переменный ток. В настоящее время эффекты Джозефсона не только подтверждены экспериментально, но и используются в микроэлектронике. 4. Теория сверхпроводимости. Ее построили в 1957 году Джон Бардин, Леон Кулер и Джон Шриффер. По первым буквам их фамилий ее назвали БКШ – теорией. В основе БКШ - теории лежит представление, что между электронами проводимости металла могут действовать силы притяжения, возникающие вследствие поляризации ими кристаллической решетки. Электрон, движущийся в решетке, притягивает к себе положительно заряженные ионы, несколько сближая их, и тем самым создает вдоль пути своего следования избыточный положительный заряд поляризованной решетки, к которому могут быть притянуты другие электроны. Это эквивалентно возникновению силы притяжения между электронами, только действующей не непосредственно, а через поляризованную решетку. Можно предположить, что сверхпроводимость следует ожидать прежде всего у тех металлов, у которых имеет место сильное взаимодействие электронного газа с решеткой, приводящее в обычных условиях к высокому удельному сопротивлению. И действительно, из чистых металлов лучшими сверхпроводниками оказались наиболее высокоомные - свинец Рb, ниобий Nb, олово Sn, ртуть Hg. В то же время у таких низкоомных металлов, как медь Cu и серебро Ag, у которых электронный газ имеет высокую подвижность, сверхпроводимости не наблюдается. Как показал Леон Купер, при Т < Ткр, самые верхние электроны, расположенные на уровне Ферми, могут спариваться. При этом их суммарная энергия оказывается меньше суммы энергий отдельных электронов. Выделяющаяся энергия должна отводиться от кристалла охлаждением. Понижение энергии куперовских пар приводит к понижению верхнего занятого электронами уровня. В результате между уровнями куперовских пар и ближайшими свободными уровнями возникает запрещенная зона шириной 2 D (рис.96 слева). Эта возникшая энергетическая щель не позволяет куперовским парам электронов принимать малую энергию. Они могут принять лишь энергию не менее 2 D, которая позволит электронам перепрыгнуть через эту щель. Поэтому при Т < Ткр куперовские пары оказываются весьма устойчивыми. При Т < Ткр спариваются не все электроны. При каждой температуре устанавливается некоторое равновесное соотношение между концентрациями нормальных и спаренных электронов. Оказывается, что ширина 2 D энергетической щели в сверхпроводнике зависит от количества неспаренных электронов. Их концентрация понижается с уменьшением температуры и соответственно растет ширина щели (рис.96 справа). Электроны, образующие куперовские пары, имеют противоположные спины. Поэтому спин пары равен нулю, и она представляет собой бозон. Бозоны могут накапливаться в основном энергетическом состоянии, из которого их трудно перевести в возбужденное состояние. Поэтому куперовские пары в состоянии согласованного движения могут оставаться неопределенно долго. Такое согласованное движение пар и есть ток сверхпроводимости. Расстояние между электронами пары велико. Оно составляет примерно 1000 нм, что около 5000 поперечников атомов. Примерно 1000 пар перекрываются, занимая общий объем. 5. Объяснение БКШ – теорией эффекта критического тока. У известных сверхпроводников величина энергетической щели составляет в среднем 2 D =3мэВ» 3·10-3·1,6·10-19Дж»5·10-22Дж. Для разрушения куперовской пары один из электронов пары должен уменьшить энергию своего движения, по крайней мере, на величину 2 D. Предположим, что электрон отдает эту энергию при лобовом столкновении с узлом решетки так, что после столкновения он отскакивает с той же скоростью дрейфа uд в обратном направлении. Энергия электрона до соударения Ек1=me (uф+ uд)2/2, энергия после соударения Ек2=me (uф - uд)2/2. Здесь uф – тепловая скорость электронов на уровне Ферми (»106м/с), uд – скорость дрейфа электронов в электрическом поле, она не превышает 1м/с. Убыль кинетической энергии электрона должна быть по крайней мере равной 2 D. Так что DЕк = Отсюда, минимальная скорость дрейфа uд, необходимая для разрушения куперовской пары, есть uд = Плотность электронного тока проводимости есть j = e·n·uд, (13.5) где n – концентрация электронов проводимости в металле. Представив критическую скорость дрейфа из (13.4), получаем критическую плотность тока jкр. jкр = enuд = e·n У типичных сверхпроводников n = 3·1028м-3, uф = 106м/с, 2 D = 3мэВ. Подставляем. jкр = 6. Объяснение БКШ - теорией критического магнитного поля. При помещении сверхпроводника в магнитное поле В в поверхностном слое сверхпроводника наводится незатухающий ток. Этот незатухающий ток имеет такие величину и направление, что его магнитное поле внутри сверхпроводника полностью компенсирует внешнее поле В. При увеличении поля В плотность компенсирующего тока в сверхпроводнике растет. Если внешнее поле В будет на столько больше, что плотность наведенного им индукционного тока достигнет критического значения, сверхпроводимость разрушается. Все выше сказанное относится к сверхпроводникам 1-го рода, в которых электрический ток существует только в приповерхностном слое. Несколько позже были открыты и изучены сверхпроводники 2-го рода. В них возникающие во внешнем магнитном поле В сверхпроводящие токи текут не только по поверхности, но и проникают в толщу проводника. У сверхпроводников 1-го рода критичное магнитное поле Вкр не превышает 0,1Тл, а у сверхпроводников 2-го рода достигает величины Вкр»20Тл. 7. Эффекты Джозефсона объясняются БКШ - теорией как результат туннелирования куперовских пар из одного сверхпроводника в другой через узкую щель, разделяющую эти куски. Как следует из теории, частота n переменного сверхпроводящего тока, определяется выражением: n = где V – напряжение на щели. При V =1мВ n =485ГГц, что соответствует длине волны ЭМ излучения l= с/n = 0,6мм. 8. Реактивное сопротивление сверхпроводника. При любой температуре Т < Ткр сверхпроводник практически всегда содержит как сверхпроводящие с концентрацией nc, так и нормальные (nн) электроны. Если поместить сверхпроводник в высокочастотное поле, то в этом переменном электрическом поле ускоряются не только куперовские пары, но и нормальные электроны. Поэтому ток имеет как сверхпроводящую, так и нормальную составляющую. Те и другие электроны обладают массой, вследствие их инерции ток отстает по фазе от напряженности ВЧ – поля. Куперовские пары движутся в проводнике как бы без трения. Согласно классической механике, скорость частиц в этом случае отстает по фазе от действующей на них периодической силы на p /2. Поэтому сверхпроводящая составляющая высокочастотного тока отстает от напряженности поля на p /2. Это значит, что куперовские пары создают чисто реактивное сопротивление. Нормальные электроны движутся как бы с трением. Поэтому они создают как реактивное, так и активное сопротивление.
|
||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 542; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.95.236 (0.011 с.) |

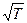 , квантовая теория дает правильный прогноз линейной зависимости r ~ Т. При температурах металла Т ³ 50К
, квантовая теория дает правильный прогноз линейной зависимости r ~ Т. При температурах металла Т ³ 50К . Переход в сверхпроводящее состояние происходит не плавно, а скачкообразно при некоторой температуре Ткр, которую называют критической температурой перехода.
. Переход в сверхпроводящее состояние происходит не плавно, а скачкообразно при некоторой температуре Ткр, которую называют критической температурой перехода.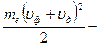
 =2 meuф·uд =2 D. (13.3)
=2 meuф·uд =2 D. (13.3)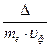 . (13.4)
. (13.4)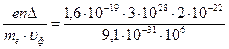 =1012
=1012 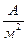 . Это соответствует току 106А через проводник сечением 1мм2. Но в реальном сверхпроводнике ток течет лишь в тонком приповерхностном слое толщиной около 35 нм, что соответствует сечению s =10-4мм2. Поэтому критический ток в сверхпроводнике толщиной около 1мм составляет всего лишь iкр= jкр·s =106А/мм2·10-4мм2=100А. Это вполне соответствует эксперименту.
. Это соответствует току 106А через проводник сечением 1мм2. Но в реальном сверхпроводнике ток течет лишь в тонком приповерхностном слое толщиной около 35 нм, что соответствует сечению s =10-4мм2. Поэтому критический ток в сверхпроводнике толщиной около 1мм составляет всего лишь iкр= jкр·s =106А/мм2·10-4мм2=100А. Это вполне соответствует эксперименту.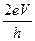 , (13.7)
, (13.7)


