
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корпускулярно-волновая природа света и частиц
1. Волны де Бройля. К двадцатым годам 20-го столетия в физике окончательно утвердилось понимание того факта, что свет имеет двойственную природу. В таких явлениях, как интерференция, дифракция, поляризация свет ведёт себя как волна. А в явлениях фотоэффекта и эффекта Комптона свет ведёт себя как поток частиц. В корпускулярном проявлении каждая световая частица – фотон – характеризуется двумя величинами: энергией hν и импульсом hν/с. Если свет ведёт себя как волна, он описывается уравнением плоской монохроматической волны В 1924 г. француз Луи де Бройль выдвинул гипотезу, что корпускулярно-волновой дуализм (двойственность) присущ не только микрообъектам полевой формы материи (фотонам), но и микрообъектам, которые традиционно понимались до этого как частицы (масса покоя не равна нулю). То есть к электронам, ядрам, атомам. Иначе, дуализм есть универсальное свойство материи. По мысли Де Бройля, каждой так называемой частице для описания её волновых свойств нужно поставить в соответствие некоторую волновую функцию ψ (как функцию Е, соответствующую фотону). Эта функция ψ (функция Де Бройля) также описывает плоскую монохроматическую волну, распространяющуюся в направлении скорости Импульс фотона
Чем больше импульс частицы, тем меньше его дебройлевская длина волны. Например, для электрона, ускоренного разностью потенциалов 100 В, λ = 0,12 нм, для протона при тех же условиях λ = 0,003 нм. Идею волновых свойств микрочастиц де Бройль использовал для объяснения правила квантования орбит в атоме Бора. Он предположил, что стационарными орбитами электронов в боровском атоме водорода являются те, которых укладывается целое число длин волн Де Бройля.
Если движение электрона по орбите рассматривать как волну материи, распространяющуюся вокруг ядра в направлении движения электрона, то на стационарной орбите волна при обходе ядра будет всякий раз возвращаться в исходную точку с той же фазой и амплитудой. В каждой точке орбиты установится постоянный колебательный режим, и потому не возникнет излучения (как в замкнутом идеальном колебательном контуре). Условие квантования принимает вид:
Здесь r – радиус круговой орбиты электрона. Так как 2. Дифракция электронных пучков в опытах Девиссона-Джермера. В 1927 г. американцы Клинтон Девисон и Лестер Джермер исследовали отражение электронов от монокристалла никеля. Установка включала в себя монокристалл никеля, сошлифованный, как показано на рис. 10, и установленный на держателе. На плоскость шлифа направлялся перпендикулярно пучок монохроматических электронов. Скорость электронов определялась напряжением U на электронной пушке: Под углом θ к падающему пучку электронов устанавливался цилиндр Фарадея, соединённый с чувствительным гальванометром. По показаниям гальванометра определялась интенсивность отражённого от кристалла электронного пучка. Вся установка находилась в вакууме. Металлический никель (Ni, z = 28, Mr = 58,7) может существовать в двух кристаллических модификациях (α и β). Обычное состояние – β -модификация, кубическая гранецентрированная решётка с постоянной а = 0,35 нм. Если у кристалла срезать угол, как показано на рис. 10, то атомы в плоскости цилиндра приобретают ось симметрии 3-го порядка. Это значит, что при повороте кристалла на держателе (менялся азимутальный угол φ) через каждые 120° атомы в плоскости цилиндра принимали тождественное положение. Расстояние между атомами в плоскости шлифа равно В опытах измерялась интенсивность рассеянного кристаллом электронного пучка в зависимости от угла рассеяния θ (0< θ <90°), от азимутального угла φ (0≤ φ ≤360°), от скорости v электронов в пучке. Электроны, падающие на кристалл, при энергиях не более 80 эВ не проникают внутрь. Они отражаются от плоскости шлифа как свет от отражательной дифракционной решётки. Штрихи решётки формируются рядами атомов А 1 А 2... Расстояние между рядами (постоянная решётки)
Опыты показали, что имеется ярко выраженная селективность рассеяния электронов. Первый максимум наблюдался при углах Рассмотрим в качестве примера следующие данные. При напряжении на электронной пушке U = 54 В первый максимум интенсивности наблюдался под углом
Длина волны де Бройля для электронов равна
Гипотеза Де Бройля нашла опытное подтверждение. 3. Дифракция электронных пучков в опытах Дж. П. Томсона. В 1928 г. Джордж Паджет Томсон (сын Дж. Дж. Томсона, открывшего в 1897 г. электрон) поставил опыт по дифракции электронных пучков при прохождении их через металлическую фольгу. Узкий моноэнергетический пучок электронов направлялся из электронной пушки на листок очень тонкой золотой фольги толщиной около 0,1 мкм. Чтобы электроны меньше поглощались и могли проходить сквозь фольгу, они разгонялись в электрическом поле с напряжением U в несколько десятков киловольт. Рассеянные на фольге электроны попадали на фотопластинку ФП (рис. 12, вверху). Опыты показали, что после проявления экспонированной в электронном пучке фотопластинки на ней появлялись концентрические тёмные кольца. Механизм их появления можно объяснить так. Полученная по обычной технологии из отливки и прокатанная золотая фольга состоит из множества мелких хаотично ориентированных кристалликов размером около 0,01 мкм. На пути электронного пучка оказывается множество граней таких кристалликов со всевозможной ориентацией. В одних случаях электрон проходит сквозь такой микрокристалл, в других – упруго отражается от него. В результате возникает хаотическое рассеяние электронов, создающее диффузное потемнение фотопластинки. Но в тех случаях, когда грань кристалла образует с осью падающего электронного пучка угол скольжения φ, соответствующий дифракционному максимуму по формуле Вульфа-Брэгга
где d – расстояние между атомными плоскостями, в направлении угла 2 φ в рассеянном пучке реализуется дифракционный максимум (рис. 12, внизу). Как и рентгеновские пучки электроны дифрагируют на атомных плоскостях, параллельных грани кристалла. В направлении угла 2 φ на фотопластинке на фоне вялого диффузного потемнения образуется от грани кристалла интенсивное чёрное пятно. Множество таких кристалликов благодаря осевой симметрии относительно пучка АО образуют в статистике концентрические кольца (рис. 13). Если радиус кольца r, а расстояние от фольги до фотопластинки L, то, учитывая малость значений углов φ, можно записать равенство.
Изменяя напряжение U в электронной пушке, можно менять скорость электронов v и, тем самым, соответствующую электронам дебройлевскую длину волны λ. Радиус r кольца будет меняться. Но согласно (3.5), при сохранении геометрии установки неизменной (L = const) отношение r/λ для одного и того же кольца будет оставаться постоянным.
Измерения показали, что отношение r/λ в опытах действительно сохраняется. В опытах Девиссона-Джермера использовались пучки относительно медленных электронов, которые разгонялись в поле напряжением U не более 100 В. Их скорость вычислялась по классической формуле eU = mv 2/2 и не превышала 2% от скорости света. В опытах Томсона использовались пучки электронов высоких энергий
Здесь β = v/с, Например, в одном из опытов было U = 54,3 кВ. Скорость электронов, вычисленная по формуле (3.6), равна Для вычисления длины волны Де Бройля в формулу Поскольку электроны в опытах Томсона имеют энергию десятки кэВ, то при их торможении на фольге могут генерироваться рентгеновские лучи. Поэтому возникает опасение, что картина на фотопластинке образуется дифракцией Х-лучей. Для устранения сомнений Томсон создавал перед фотопластинкой магнитное поле. В результате картина, создаваемая электронами, смазывалась. Таким путём можно всегда отличить электронные дифракционные кольца от колец рентгеновских лучей. Итак, опыты Томсона показали, что при рассеянии электронов на тонкой металлической фольге они (электроны) проявляют волновые свойства с длиной волны Де Бройля. 4. Дифракция отдельных электронов. Опыты Дэвиссона-Джермера и Томсона подтвердили формулу дебройлевской длины волны (3.1). Однако эти опыты были выполнены с электронными пучками больших интенсивностей, в которых концентрация электронов была настолько велика, что их нельзя было считать системой невзаимодействующих частиц. Поэтому оставалось допущение, что дифракция электронного пучка есть свойство коллектива электронов, а не отдельных электронов. Чтобы снять сомнения, Л. Биберман, Н. Сушкин и В. Фабрикант в 1949 г. поставили опыт с электронными пучками столь малых интенсивностей, что электроны проходили через мишень заведомо поодиночке. Паузы были в 30000 раз продолжительнее времени прохождения электрона. Результаты опытов вновь подтвердили формулу Де Бройля. 5. Соотношение неопределённостей Гейзенберга. Из анализа накопленного к концу двадцатых годов экспериментального материала следовало, что есть явления, в которых электроны ведут себя как частицы. Это, например, движение электронов в катодных лучах, в электронно-лучевых трубках, в камере Вильсона. Здесь их движение может быть описано в понятиях классической механики, а сами электроны могут моделироваться материальными точками.
Но есть такие явления, в которых положение электронов в пространстве определяются вероятностными законами. Это, например, рассеяние электронов на кристаллах. Здесь нельзя говорить о траекториях их движения, поскольку исчезает механическая однозначность в поведении микрообъектов. Если рассмотреть дифракционные кольца на фотопластинках в опытах Томсона под микроскопом, то все эти кольца распадаются на кольцевые системы точечных почернений. Каждая черная микроточка образуется при поглощении единичного электрона. Таким образом, отдельный электрон никаких дифракционных колец не дает, он поглощается как частица. Дифракционные кольца образуются разной густотой электронных следов. В местах дифракционных максимумов густота больше, в местах минимумов – меньше. В какую точку попадёт электрон, сказать однозначно нельзя. На вопрос: каковы критерии применимости классической или квантовой модели – ответил в 1927 г. немец Вернер Гейзенберг. Он открыл соотношение неопределённостей для координаты и импульса микрочастиц. Он рассуждал примерно так. Чтобы определить поглощение и импульс электрона, нужно осветить его и получить хотя бы один рассеянный при столкновении фотон. Вследствие дифракции погрешность определения координаты электрона не может быть меньше длины волны фотона, ∆x ≈ λ. Чем точнее нужно определить положение электрона, тем меньше должно быть λ, тем более жёстким будет фотон. При столкновении с фотоном электрон получает отдачу, которая тем больше, чем больше импульс фотона h/λ. Итак, уменьшая погрешность в координате ∆x, мы увеличиваем погрешность в импульсе ∆рx, и наоборот. Обычно соотношение неопределённостей записывают для проекций импульса и координат.
Гейзенберг, 1927г.
Здесь ∆ р и ∆ х, ∆ y, ∆ z – среднеквадратичные отклонения этих величин от их средних значений. Из соотношения неопределённостей следует, что чем точнее определена одна из входящих в неравенство величин, тем менее определённым становится значение другой. Никакой эксперимент не может дать одновременно точные значения координаты и импульса микрочастицы. Дальнейшее развитие квантовой механики показало, что суть соотношения неопределённостей не в том, что несовершенны измерительные системы. Суть в том, что неопределённость координаты и импульса есть объективное свойство материи. Соотношение неопределённостей Гейзенберга указывает границы корректности вопросов, которые можно задавать природе. Соотношение неопределённостей можно записать еще для двух величин – энергии Е и времени t.
Произведение энергии на время называют действием. Поэтому выражение ∆ E ∆ t называют неопределённостью действия. Соотношение неопределённостей (3.8) выражает принцип соответствия. Если Если система находится в стационарном состоянии, то есть в состоянии, которое при отсутствии внешних сил не меняется, то энергию системы в этом состоянии можно измерить лишь с погрешностью не менее h/ ∆ t, где ∆ t – длительность процесса измерения. Если же система нестационарна, то неопределённость значения энергии не может быть меньше h/ ∆ t, где ∆ t – характерное время, в течение которого существенно меняются средние значения физических параметров этой системы. 6. Микрочастицы и принцип наглядности. С развитием квантовой физики пришлось отказаться от наглядности физических моделей. Рассмотрим мысленный эксперимент по дифракции электронов на двух отверстиях. Мысленный потому, что диаметр отверстий должен быть одного порядка с диаметром атома водорода, что технически трудно сделать. Однако дифракция электронов на атомных плоскостях показывает, что события должны развиваться именно так. Рассмотрим дифракцию электронов по схеме Юнга. На пути электронного пучка находится экран Э1 с двумя отверстиями 1 и 2. Далее по ходу движения электронов находится экран Э2 с фотопластинкой ФП (рис. 14, вверху). Мысленно представим, что электроны поодиночке проходят через 1-е отверстие Если же открыть оба отверстия, то получится не сумма дифракционных картин отдельных отверстий, а дифракционная картина на двух отверстиях сразу (рис. 14, внизу справа). Получается, что каждый электрон проходит одновременно через оба отверстия. В то же время во всех явлениях электрон – целостный не дробящийся объект. Ситуация ненаглядна. Но это объективное свойство квантовых моделей. Уравнение Шрёдингера 1. Уравнение Шрёдингера. В 1925 г. австрийский физик Эрван Шрёдингер, основываясь на общих соображениях, сконструировал дифференциальное уравнение для волновой функции Де Бройля (подробнее см. [1], с.с. 137-178).
Здесь Для систем в стационарном состоянии, когда все наблюдаемые физические параметры не меняются с течением времени, уравнение Шрёдингера имеет вид:
Здесь E – полная энергия системы. В случае стационарного поля она остаётся постоянной. Уравнение Шрёдингера является основным уравнением нерелятивистской квантовой механики. Его справедливость доказывается тем, что все вытекающие из него следствия очень хорошо согласуются с ответом. Поэтому до настоящего времени уравнение Шрёдингера вызывает у некоторых физиков чувство полумистического восхищения. 2. Вероятностный смысл функции Ψ. В том же 1926 г. немец Макс Борн показал, что функция Ψ имеет вероятностный смысл. Квадрат модуля волновой функции
Из вероятностного смысла волновой функции Ψ следует, что квантовая механика имеет статистический характер. Она не позволяет определить положение частицы в пространстве или определить траекторию её движения. В рамках квантовой механики ставить вопрос о точном местонахождении частицы или о траектории её движения некорректно. С помощью волновой функции Ψ можно лишь предсказать, с какой вероятностью частица может быть обнаружена в разных по величине и положению объёмах пространства. 3. Частица в одномерной потенциальной яме. Математический аппарат квантовой механики очень труден. Число задач, в которых уравнение Шрёдингера решается точно, невелико. В большинстве задач решения приближённые. Они изучаются в курсах теоретической физики. Самая простая задача о движении частицы в одномерной потенциальной яме рассматривается здесь для того, чтобы познакомиться с некоторыми понятиями квантовой механики и убедиться в том, что условия квантования энергии заложены в самом уравнении Шрёдингера. Рассмотрим состояние частицы в одномерной бесконечно глубокой прямоугольной потенциальной яме. Это значит, что потенциальная энергия U частицы удовлетворяет условиям:
Здесь l – длина потенциальной ямы вдоль оси ОX. Так как в задаче нет изменяющихся во времени силовых полей, то она соответствует уравнению Шрёдингера для стационарных состояний (4.2). В декартовых координатах, в которых составлена задача, выражение ∆Ψ имеет вид:
Задача одномерная, члены, содержащие переменные y и z, выпадают. Уравнение (4.2) упрощается. (Напомним, что в яме U = 0).
Покажем, что стенки ямы непроницаемы для частицы. Выйти за пределы ямы она не может. Отсюда следуют граничные условия для волновой функции Ψ.
Обозначим коэффициент
Это уравнение напоминает уравнение движения незатухающего гармонического осциллятора. Разница в том, что в осцилляторе независимая переменная – время t. Здесь независимая переменная – координата x. Решение уравнения (4.8) имеет вид:
4. Квантование энергии. Найдём по условиям задачи постоянные интегрирования А и α. Воспользуемся вначале краевыми условиями (4.7).
Из первого условия вытекает Из второго условия также нельзя определить амплитуду А. Но из него вытекает условие квантовой энергии частицы. Действительно,
Условие n = 0 нужно исключить, так как здесь получается Итак, из условия (4.11) следует:
В уравнении Шрёдингера уже заложен дискретный спектр значений энергии частицы Е. Уравнение Шрёдингера (4.8) имеет решение не при любых значениях Е, а лишь при некоторых, определяемых формулой (4.12). Эти избранные значения Е называются собственными значениями параметра, в данном случае, собственными значениями энергии Е. 5. Нормировка волновой функции. Вторая постоянная интегрирования – амплитуда А функции Ψнаходится из условия нормировки. Суть этого условия в том, что достоверно известно, что частица находится в яме. Вероятность P пребывания частицы в яме равна 1.
Так как
Итак, Решение уравнения (4.8) имеет вид:
Значения Ψ, удовлетворяющие уравнению Шрёдингера, называются собственными функциями уравнения Шрёдингера. На рис. 16а слева показан график функции Ψ в яме при разных квантовых числах n = 1, 2, 3, … То, что значения Ψ в каждой точке пространства не меняется во времени (стационарная задача) позволяет толковать её как стоячую волну, образованную сложением бегущей волны (слева направо) с упруго отражённой от стенки x = l (справа налево). При n = 1 наиболее вероятное пребывание частицы в области середины ямы x = l/ 2. При n = 2 обнаружить частицу в центре маловероятно. Зато с одинаковой вероятностью можно найти её вблизи центров x = l/ 4 и x =3 l/ 4 «половинок» ямы. Длина волны λ, характеризующая волну Ψ, найдётся из уравнения: 6. Коплексная форма функции Ψ. Пусть вдоль оси ОХ двигается фотон с энергией
Физически здесь А – напряжённость электрического поля волны. Фазу волны
Волновая функция фотона есть
То, что величина А есть напряжённость электрического поля, для описания волновых свойств фотона не имеет принципиального значения. Выражение (4.18) можно формально применить для описания волновых свойств и других нейтральных частиц – нейтрино, нейтрона... Для описания волновых свойств электрически заряженных частиц в волновую функцию добавляется ещё мнимая часть.
Здесь то Квадрат модуля комплексной функции 7. Ротатор. Квантование момента импульса. Ротатором в квантовой механике называется неизменная вращающаяся система, состоящая из частицы массой m c угловой степенью свободы. То есть полагается, что частица может двигаться по окружности радиуса r со скоростью v. Координатой движения является угол поворота φ. Поскольку система квантовая, то по окружности движения частицы должна распространятся волна Де Бройля. Решение уравнения Шрёдингера для обоснований условий квантования момента импульса ротатора является сложной математической задачей. Поэтому сформулируем здесь основные итоги. В отличие от классической механики в квантовой механике определённые значения одновременно могут иметь только квадрат момента импульса L 2 и одна из проекций момента импульса на координатную ось, например Lz. а. Квадрат момента импульса L 2 принимает дискретный ряд значений,
так называемое азимутальное квантовое число. В зависимости от энергетического уровня число l может принимать значения от 0 до п – 1, где п – главное квантовое число. б. Проекция момента импульса на произвольную ось Z также принимает дискретный ряд значений,
так называемое магнитное квантовое число. в. Проекция момента импульса на произвольную ось Z не может превосходить его модуля Отсюда следует, что максимально возможное значение числа Заметим, что произвольная ось Z задаётся в эксперименте обычно с помощью электрического или магнитного поля. В этом случае в качестве оси Z берут направление силовых линий поля. Неопределённость ориентации момента импульса L квантовой системы не есть лишь свидетельство размытости момента импульса в пустом пространстве. Оно остаётся неопределённым и при наличии внешнего воздействия со стороны поля. Квантовое число m определяет ориентацию момента импульса L относительно Если l увеличить, например l = 2, то модуль L также увеличивается, Заметим, что углы между векторами 8. Принцип причинности в квантовой механике. Классическая механика, описывая движение макротел, создаёт детерминированную, то есть причинно собственную картину мира. Это означает следующее. Пусть имеется система конечного числа материальных точек m 1, m 2, …mi в определённом силовом поле. Известно уравнение движения каждой материальной точки этой системы.
Здесь к – число частиц в системе, Принцип причинности утверждает, что если известны начальные условия этой системы, то есть координаты и импульсы всех материальных точек в некоторый момент времени, то состояние системы определено на любой момент времени как в прошлом, так и в будущем. Положение не меняется, если в систему входят не только материальные точки, но и тела. Нужно лишь, чтобы их механические параметры были известными. Исходя из открытого им принципа неопределённостей, Гейзенберг предположил, что принцип причинности в микромире нарушается. Поскольку нельзя однозначно определить координаты и импульсы микрочастиц в системе, то по мнению Гейзенберга, нельзя и спрогнозировать состояние микросистемы на какой-то момент времени. Представляется, что этот вывод Гейзенберга неверен. Дело в том, что при переходе от макро- в микромир меняется группа понятий, описывающих состояние системы. Происходит переход от координаты и импульса к волновой функции Ψ. Причинность приобретает статистический характер. Динамический детерминизм переходит в статистический детерминизм. 9. Туннельный эффект – это чисто квантовое явление. Суть его в том, что микрочастица способна преодолевать энергетический барьер не только в тех случаях, когда её полная энергия Е больше потенциальной энергии U барьера. Это обычно в классической механике (инфинитное движение). Оказывается, существует отличная от нуля вероятность обнаружить микрочастицу с энергией E<U по другую сторону барьера, что в классической механике исключено. Рассмотрим два случая. а. Взаимодействие частицы с потенциальным барьером. Пусть частица с полной энергией Е движется вдоль оси ОХ и взаимодействует с энергетическим барьером, высота которого U>E (рис. 17, вверху). В общем случае вопрос ставится так: каков коэффициент отражения R частицы от стенки барьера и какова плотность вероятности Вначале, решая уравнение Шрёдингера, отыскиваются волновые функции Ψ1и Ψ2 в областях 1 и2. Поскольку Ψ – функция вдоль оси ОХ должна быть непрерывной, решения Ψ1иΨ2 на границе барьера в точке х = 0 «склеиваются». Оказалось, что коэффициент отражения частицы от барьера R = 1, а коэффициент пропускания T = 1 – R = 0. Это соответствует классическим представлениям. Но плотность вероятности обнаружить частицу за барьером не равна нулю. Она определяется выражением:
Здесь m – масса частицы. На рис. 17 внизу показана зависимость Итак, микрочастицы отражаются от потенциального барьера, но не как от непроницаемой стенки, а проникая на некоторую глубину. Это похоже на полное внутреннее отражение световой волны на границе с оптически менее плотной средой, когда волна «провисает» сквозь границу на некоторую глубину, соизмеримую с длиной λ. б. Взаимодействие частицы с барьерной стенкой конечной толщины. Пусть частица с энергией Е, двигаясь вдоль оси ОХ, взаимодействует со стенкой высотой U>E и толщиной d (рис. 18, вверху). Области 1 и 3 по обе стороны стенки одинаковы. Оказалось, что коэффициент пропускания Т определяется выражением:
Так как Т ≠ 0, то R ≠ 1. Не всегда микрочастица отражается от стенки. Существует отличная от нуля вероятность, что частица пройдёт сквозь стенку. Плотность вероятности Прохождение через потенциальный барьер не сопровождается изменением энергии частицы. Она выходит из пределов барьера с той энергией, с какой в него попадает. В выражении «туннельный эффект» подчёркивается тот факт, что частица не взбирается на вершину барьера. Она проходит сквозь него.
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 587; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.83.150 (0.103 с.) |
 . Физический смысл величины Е зависит от того, в какой модели рассматривается свет. В эфирной модели Е – это смещение частиц эфира относительно положения равновесия. В ЭМ модели Е – это напряжённость электрического поля в точках оси ОХ в моменты времени t.
. Физический смысл величины Е зависит от того, в какой модели рассматривается свет. В эфирной модели Е – это смещение частиц эфира относительно положения равновесия. В ЭМ модели Е – это напряжённость электрического поля в точках оси ОХ в моменты времени t. движения частицы. Хотя физический смысл функции ψ оставался ещё неясным, тем не менее к корпускулярным характеристикам частицы – энергии и импульсу – можно было добавить по аналогии некоторые волновые. Например, длину волны.
движения частицы. Хотя физический смысл функции ψ оставался ещё неясным, тем не менее к корпускулярным характеристикам частицы – энергии и импульсу – можно было добавить по аналогии некоторые волновые. Например, длину волны. . Отсюда, длина волны фотона с импульсом p есть
. Отсюда, длина волны фотона с импульсом p есть 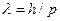 . Применительно к частице её импульс p = mv. Отсюда
. Применительно к частице её импульс p = mv. Отсюда Длина волны Де Бройля (3.1)
Длина волны Де Бройля (3.1) где n = 1, 2, 3,... (3.2)
где n = 1, 2, 3,... (3.2) то
то 
 (3.3)
(3.3) .
. (рис. 11).
(рис. 11).
 . При изменении азимутального угла φ максимумы повторялись через 120°.
. При изменении азимутального угла φ максимумы повторялись через 120°. при k = 1
при k = 1 
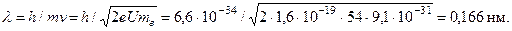
 (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6)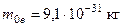 – масса покоя электрона.
– масса покоя электрона.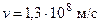 , что около половины скорости света с.
, что около половины скорости света с. нужно подставлять релятивистскую массу электрона
нужно подставлять релятивистскую массу электрона  В нашем примере длина
В нашем примере длина 
 Соотношение неопределённостей для координат – импульса. (3.7)
Соотношение неопределённостей для координат – импульса. (3.7) . Принцип соответствия (3.8)
. Принцип соответствия (3.8) , явление описывается классическими законами, при
, явление описывается классическими законами, при  – квантовыми.
– квантовыми. . Общее уравнение Шрёдингера (4.1)
. Общее уравнение Шрёдингера (4.1) – мнимая единица, ħ=h/2π, m – масса частицы, U – потенциальная энергия частицы, функция координат, t – время, ∆ – оператор Лапласа.
– мнимая единица, ħ=h/2π, m – масса частицы, U – потенциальная энергия частицы, функция координат, t – время, ∆ – оператор Лапласа. . Уравнение Шрёдингера для стационарных состояний (4.2)
. Уравнение Шрёдингера для стационарных состояний (4.2) определяет плотность вероятности p нахождения частицы в точке пространства,
определяет плотность вероятности p нахождения частицы в точке пространства,  . Вероятность P нахождения частицы в объёме пространства V находится интегрированием.
. Вероятность P нахождения частицы в объёме пространства V находится интегрированием.
 (4.3)
(4.3) (4.4)
(4.4) (4.5)
(4.5) или
или  (4.6)
(4.6)
 (4.7)
(4.7) Тогда
Тогда (4.8)
(4.8) (4.9)
(4.9)
 (4.10)
(4.10) (Случай А = 0 приводит к тому, что
(Случай А = 0 приводит к тому, что 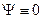 в любой точке ямы. Но это возможно лишь при отсутствии там частицы, что противоречит условию задачи).
в любой точке ямы. Но это возможно лишь при отсутствии там частицы, что противоречит условию задачи). При
При  и
и  отсюда следует:
отсюда следует:
 где n = 1, 2, 3,... (4.11)
где n = 1, 2, 3,... (4.11) А это значит Ψ = 0 при любых x.
А это значит Ψ = 0 при любых x.
 (4.12)
(4.12) (4.13)
(4.13) то
то

 (4.14)
(4.14) (4.15)
(4.15)

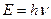 и импульсом
и импульсом 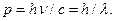 В классическом приближении фотону соответствует электромагнитная волна – бесконечная синусоида.
В классическом приближении фотону соответствует электромагнитная волна – бесконечная синусоида. (4.16)
(4.16) можно представить через энергию и импульс фотона. Так как
можно представить через энергию и импульс фотона. Так как 
 то
то (4.17)
(4.17) (4.18)
(4.18) (4.19)
(4.19) (4.20)
(4.20) (4.21)
(4.21) есть произведение этой функции Ψ на сопряжённую Ψ *.
есть произведение этой функции Ψ на сопряжённую Ψ *. где l = 0, 1, 2, … (4.22)
где l = 0, 1, 2, … (4.22) где m = 0, ±1, ±2, … (4.23)
где m = 0, ±1, ±2, … (4.23) или
или 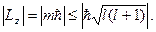 (4.24)
(4.24) как целого числа равно l. Даже при m = l
как целого числа равно l. Даже при m = l  Это обусловлено тем, что направление момента импульса в пространстве является неопределённым.
Это обусловлено тем, что направление момента импульса в пространстве является неопределённым. Это радиус сферы, в которой вписаны три конуса с вершинами в центре сферы. При m = 0 конус вырождается в диск, Lz = 0. При m=+1 получаем конус в верхней части, его высота Lz равна +ћ. При m = – 1 получаем конус в нижней части, его высота Lz = –ћ. То, что известна одна проекция на ось, можно толковать так, что вектор
Это радиус сферы, в которой вписаны три конуса с вершинами в центре сферы. При m = 0 конус вырождается в диск, Lz = 0. При m=+1 получаем конус в верхней части, его высота Lz равна +ћ. При m = – 1 получаем конус в нижней части, его высота Lz = –ћ. То, что известна одна проекция на ось, можно толковать так, что вектор  прецессирует по стенке конуса.
прецессирует по стенке конуса. Радиус сферы стал больше. Но больше стало и число возможных ориентаций вектора
Радиус сферы стал больше. Но больше стало и число возможных ориентаций вектора 
 ...
...  ...
...  (4.25)
(4.25) - суммарная сила, действующая на i -тую частицу.
- суммарная сила, действующая на i -тую частицу. (4.26)
(4.26) , в глубине 0,1 нм – около 30%, в глубине 0,5 нм – 0,5%. И уже только в глубине 1 нм (10 атомных поперечников) и далее
, в глубине 0,1 нм – около 30%, в глубине 0,5 нм – 0,5%. И уже только в глубине 1 нм (10 атомных поперечников) и далее  (4.27)
(4.27)


