
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проблема строения атома. Опыты РезерфордаСодержание книги
Поиск на нашем сайте
1. Закономерности в спектрах атомного водорода. Как известно, есть три вида спектров излучения: сплошной, испускаемый нагретыми твёрдыми и жидкими телами, полосатый, испускаемый молекулярными газами, и линейчатый, испускаемый газами в атомном состоянии. Линейчатые спектры самые простые, они были изучены раньше других. В 1885 г. швейцарец Иоганн Бальмер исследовал спектр водорода. Оказалось, что в электрическом разряде при давлении не более 10 мм Hg большинство молекул водорода диссоциируют на атомы. Спектр, испускаемый атомами водорода, становится более заметным по сравнению с молекулярным. Измерив длины волн λ спектральных линий, Бальмер нашёл, что они укладываются в формулу:
Здесь m = 3, 4, 5,... ∞ – натуральное число, R – коэффициент пропорциональности, называемый постоянной Ридберга, R = 1,097·107 м–1. Бальмеру удалось наблюдать 4 линии: Hα (m = 3), λ = 656,3 нм, красная; Hβ (m = 4), λ = 486,1 нм, сине-зелёная; Hγ (m = 5), λ = 434,0 нм, фиолетовая; Hδ (m = 6), λ = 410,2 нм, фиолетовая. Наблюдать большее число линий в спектре, получаемом с помощью разрядной трубки, трудно по той причине, что газ в трубке сильно разрежён. Из-за этого на пути луча оказывается мало излучающих атомов. Интенсивность света очень низкая, тем более, что с ростом m яркость спектральных линий уменьшается. С целью повышения интенсивности исследуемый пучок света стали формировать вдоль разрядной трубки, увеличивая её длину до 1-2 м. В 1920 г. Роберт Вуд сфотографировал 22 линии серии Бальмера. Максимальное число линий, 37, удалось сфотографировать в спектре солнечной короны. Здесь водород очень разрежён, поэтому газ находится исключительно в атомном состоянии. Но за счёт гигантской протяжённости короны интенсивность света достаточно высокая. Соответствие формулы (1.1) эксперименту поразительно. Расхождение в значениях вычисленных и измеренных λ появляются лишь в 5-6 знаке. На рис.1 показано расположение линий серии Бальмера в спектре. Примерно так выглядит атомный спектр водорода в спектрометре с дифракционной решёткой. С ростом m линии серии располагаются всё теснее. Минимальная длина волны серии λ = 364,7 нм при m = ∞ называется границей серии. Закономерности в спектре атомного водорода долго оставались необъяснимыми. В начале 20 в. Вальтер Ритц высказал предположение, что в спектре водорода могут быть и другие серии, определяемые формулой (1.1), в которой вместо двойки находятся числа n = 1, 3, 4,..., а m ³ n + 1. В 1906 г. американец Теодор Лайман нашёл подобную серию в ультрафиолетовой области спектра, удовлетворяющую формуле:
Позднее были открыты ещё 3 серии в ИК-области.
Все серии объединяются одной обобщённой формулой
где n = 1, 2, 3,..., m = n + 1, n + 2, n + 3,... ∞. В зависимости от значения n получается та или иная серия. n = 1, Серия Лаймана, λmax (m = 2) = 121,6 нм, λmin (m = ∞) = 91,2 нм. УФ обл. n = 2, Серия Бальмера (656,3 – 364,7 нм). Видимая область. n = 3, Серия Пашена (1875 – 820 нм). Ближняя ИК-область. n = 5, Серия Пфунда (7458 – 2278 нм). Дальняя ИК-область. На схеме рис. 2 показано относительное положение серий в спектре водорода. Длина волны λ отмечена в логарифмическом масштабе. Как видно из рисунка, только серии Лаймана и Бальмера не перекрываются. Начиная с серии Пашена, с ростом т серии спектральных линий накладываются друг на друга. В спектре поглощения водорода, атомы которого не возбуждены, присутствует только серия Лаймана. Это объясняется тем, что большинство атомов водорода находятся в основном состоянии, которое соответствует n = 1. (См. след. параграф).. 2. Проблема строения атома. Механическая модель атома как неизменной частицы материи в конце 19 века пришла в прямое противоречие с физическим опытом. В 1887 г. был открыт фотоэффект (выбивание светом из вещества электронов, Г. Герц), в 1895 г. Вильгельм Рентген открывает X-лучи (испускание ЭМ-волн электронами при их быстром торможении о метал), в 1896 г. Антуан Беккерель открывает естественную радиоактивность (испускание атомами проникающего излучения). Стало очевидно, что атом вещества имеет сложную структуру. Встал вопрос: что такое атом и как он устроен? 3. Модель атома Томсона. В 1897 г. Дж. Дж. Томсон, исследуя разряд в разрежённых газах, установил, что от катода к аноду движутся отрицательно заряженные частицы, масса которых примерно в 2000 раз меньше массы атома водорода. Так был открыт электрон. В 1904 г. Томсон предложил первую атомную модель, пригодную для количественных оценок. Согласно Томсону, атом представляет собой протяжённый шар радиусом R с равномерно и непрерывно распределёнными в нём положительным зарядом. Электроны, входящие в состав атома, находятся внутри этого заряженного шара. Суммарный заряд электронов равен заряду шара, поэтому атом в целом электронейтрален. Из модели Томсона вытекал простой механизм излучения атома водорода. Очевидно, заряд шара атома водорода e +, в нём должен находиться один электрон с зарядом e –. В невозбуждённом атоме электрон должен находиться в центре шара (рис. 3). Если электрон сместить из центра на расстояние r, то на него будет действовать электрическая возвращающая сила, равная
Здесь
Возвращающая сила квазиупругая, она пропорциональна смещению r электрона от центра шара. Под действием этой силы электрон способен совершать гармонические колебания x = A cos ω 0 t, где Ускорение, испытываемое электроном, равно Итак, атом водорода по Томсону способен излучать лишь одну монохроматическую ЭМ-волну с частотой ω 0. Он не может давать спектральную серию с бесконечным числом длин волн. Кроме того, модель Томсона не объясняет периодических свойств элементов в таблице Менделеева, природу химической связи, не объясняет α -распад и так далее. Казалось бы, в модели Томсона больше недостатков, чем достоинств. Однако её историческая роль состояла в том, что ею завершался этап догадок и предположений об атомах. Начинались целенаправленные экспериментальные и теоретические исследования. 4. Опыты Леонарда. В 1893 г. Филипп Леонард, изучая катодные лучи, впервые вывел отрицательно заряженные частицы (электроны), движущиеся в разрядной трубке от катода к аноду, через специальное окошко в воздух (рис. 4). Окошко Леонарда представляло собой тонкий листок алюминия толщиной 2-3 мкм. Чтобы листок не продавило атмосферным воздухом, он наклеивался на пластинку с отверстиями. Вылетавшие из разрядной трубки электроны улавливались цилиндром электрометра. Изменяя расстояние l между трубкой и электрометром, можно оценить характер поглощения электронов молекулами воздуха. Оказалось, что электронный пучок ослабляется в воздухе по закону Бугера
где S 0 – эффективное сечение молекул воздуха, рассеивающих электроны, N 0 – концентрация молекул. Скорость v электронов определяется напряжением U между катодом и анодом и находится из условия:
Изменяя напряжение на разрядной трубке, Ленард установил, что эффективное сечение молекул воздуха S 0 быстро уменьшается с ростом скорости движения электронов. После продолжения и углубления опытов в 1903 г. Ленард делает вывод: масса атома He распределена равномерно по его объёму. Она занимает малую часть его объёма. 5. Опыты Резерфорда. В 1909 г. Эрнст Резерфорд и его сотрудники Ганс Гейгер и Эрнст Марсден с целью уточнения размеров атомов провели серию опытов. В качестве частиц-снарядов они использовали не электроны, легко отклоняющиеся в электромагнитных полях, а тяжёлые α- частицы – двукратно ионизированные атомы гелия. В отличие от отрицательных ионов α -частицы несут положительный заряд, и потому должны отталкиваться от положительно заряженного ядра атома. Масса α -частицы примерно в 8000 раз больше массы электрона. Поэтому они должны проходить ближе к ядру и позволить тем самым более точно определить его размеры. Установка представляла собой гониометр, на оси которого крепился листок золотой фольги Au (рис. 5). Под прямым углом к плоскости фольги на некотором расстоянии от неё находился контейнер с препаратом α -активного радия 88 Ra 226. Вокруг фольги с препаратом почти на полный оборот могла поворачиваться труба микроскопа М. В фокусе объектива микроскопа крепилась стеклянная пластинка с напыленным порошком сульфида цинка ZnS. При попадании α- частицы в кристалл ZnS происходила сцинтилляция – люминесцентная вспышка зеленоватого света, наблюдавшаяся в микроскоп М. Во избежание рассеяния α- частиц на молекулах газа установка герметизировалась и из неё откачивался воздух до давления p <1 мм Hg. Относительное положение препарата Ra и фольги оставалось в процессе опытов неизменным. Измерения сводились к подсчёту числа сцинтилляций при определённых углах θ за одинаковые промежутки времени. Всего было зарегистрировано (визуально!) около 150000 вспышек. В таблице 1.1 приведены результаты измерений рассеяния α- частиц золотой фольгой.
Прежде всего бросается в глаза, что подавляющее большинство α- частиц, взаимодействующих с фольгой, отклоняется в пределах 15º. И лишь ничтожно малая часть (0,05%) отражается под углами 135-150º. Резерфорд предположил, что эти α- частицы отражаются в результате единичных лобовых соударений с ядром. Для обработки результатов Резерфорд построил количественную теорию рассеяния α- частиц. При этом он полагал, что весь положительный заряд атома Ze + сосредоточен в ядре, а электрическое взаимодействие внутри атома подчиняется закону Кулона. Результаты исследований были опубликованы в 1911 г. По характеру рассеяние α- частиц атомами металлов Резерфорд вычислил размер ядра. Его поперечник оказался в 10 000 раз меньше атома. Для сравнения: радиус Солнца ( Исходя из предположения о справедливости закона Кулона во внутриатомном масштабе, что позволяет заключить, что поле ядра изменяется по Закону E ~ 1/ r 2, Резерфорд предложил ядерную или т.н. планетарную модель атома. Атом состоит из ядра с зарядом Ze + и вращающихся вокруг него по круговым орбитам z электронов. Электрическое поле ядра подчиняется закону Кулона. 6. Единичность столкновений. Чтобы убедиться в справедливости гипотезы Резерфорда о единичности соударений α- частиц с ядрами атомов фольги, сравним общую площадь суммарного эффективного сечения ядер атомов фольги с площадью фольги. Фольга толщиной d и площадью S имеет массу m = ρSd, где ρ – плотность вещества фольги. В этой массе содержится
Здесь M – молярная масса вещества фольги, NA – число Авогадро. Объём одного атома
Диаметр 2 Ra одного атома есть ребро куба, в который этот атом заключён.
Для золота M = 0,197 кг/моль, Поперечник ядра по расчётам Резерфорда на четыре порядке меньше. Его радиус
Очевидно, Площадь эффективного сечения одного ядра
В объёме фольги толщиной d и площадью S суммарное эффективное сечение ядер в N раз больше,
Отношение суммарной площади сечения ядер к площади фольги составляет
Толщина фольги в опытах не превышала d = 1 мкм. Отсюда
Столь относительно малая площадь суммарного сечения ядер позволяет уверенно говорить о том, что ядра не заменяют друг друга, а повторное соударение α- частицы с ядром исключительно маловероятно. И лишь при движении вдоль фольги эта вероятность увеличивается. Поэтому угол 90º исключён из таблицы. 7. Проблема устойчивости атома Резерфорда. В отличие от статической модели атома Томсона атом Резерфорда динамический. Каждый электрон атома движется вокруг ядра по круговой орбите так, что центростремительная сила равна кулоновской силе притяжения электрона к ядру.
Здесь me – масса электрона, r – радиус его орбиты, z – зарядовое число ядра, то есть количество в нём элементарных положительных зарядов. Поскольку атом нейтрален, то зарядовое число ядра z равно числу электронов в атоме. Если принять, что радиус атома водорода близок к радиусу атома золота, то есть r» 10–10 м, то скорость движения электрона в атоме водорода составляет около В ядерной модели Резерфорда внутренняя структура атома приобретала знакомые из небесной механики очертания. Вокруг ядра как вокруг Солнца движутся электроны – планеты. С точки зрения механики система устойчива. В ней действуют только центральные кулоновские силы. Поэтому полная механическая энергия этой, казалось бы, консервативной системы должна оставаться постоянной. И для построения теории атома оставалось лишь применить аппарат классической механики. Но с учётом законов электродинамики планетарный атом неустойчив. Ведь электроны, движущиеся по окружностям, испытывают центростремительное ускорение.
Применительно к атому водорода Расчёты показывают, что вся энергия электрона перейдёт в энергию ЭМ волны за время Спектр ЭМ излучения, испускаемого электронами такого гибнущего атома, должен быть сплошным, а не линейчатым. Атом Бора 1. Постулаты Бора. Принципиальный отказ от механической трактовки атома сделал датский физик Нильс Бор в 1913 г, когда он сформулировал два постулата. Постулат 1. Правило квантования орбит. Электроны в атоме могут находиться не на любых энергетических уровнях, допускаемых классической механикой. Они могут находиться лишь на определённых стационарных уровнях, на которых орбитальный момент импульса электрона L = mvr кратен величине h/ 2 π.
Атом в стационарном состоянии не излучает и не поглощает энергии. Постулат 2. Правило частот. Переход электрона с одного уровня на другой сопровождается излучением или поглощением кванта энергии
Здесь Ek и Ei – энергия атома с электроном на k -том и i -том уровнях, νik – частота излучаемого или поглощаемого света при переходе электрона с одного уровня на другой. 2. Основания постулатов лежат в опытных фактах. Первый постулат, признающий существование в атомах стационарных энергетических уровней электронов, представляет собой опытный закон природы. Поскольку атомы длительное время существуют, то существуют и их состояния, в которых атомы не излучают и не поглощают. То, что классическая электродинамика не может объяснить этот факт, следует рассматривать как ограниченность электродинамики, не применимость её законов для описания внутриатомных процессов. Основанием второго постулата являются фотоэффект, тепловое излучение и сериальные закономерности в спектре атома водорода. При фотоэффекте свет поглощается квантами hν. Из законов теплового излучения следует, что излучается свет также квантами hν. Но это значит, что и спектральные линии в излучении атома водорода формируются квантами с энергией hν. Если умножить формулу Бальмера (1.6) на hc, где с – скорость света в вакууме, то получаем:
Слева стоит энергия hν кванта излучаемого атомом света, а справа – разность каких-то двух величин с размерностью энергии. Можно предположить, что выражение Rhc/π 2, где n = 1, 2, 3, 4, …, пропорционально энергии атома водорода в стационарных состояниях. В качестве обоснования условия квантования момента импульса электронов на стационарных уровнях в виде L = nh/ 2 π отметим лишь, что именно при таком квантовании из теории Бора вытекает формула Бальмера. 3. Опыты Франка и Герца. Основное положение Бора о дискретности значений энергии атома доказали экспериментально немцы Джеймс Франк и Густав Герц в 1913-14 и 1919-20 годах. Их установка представляла собой эвакуированную лампу с внесённой в неё каплей ртути (рис. 6). Лампа помещалась в печь. Изменяя температуру в печи, можно было менять давление ртутных паров в лампе. В большинстве опытов давление составляло от 1 до 30 мм Hg. Лампа включала в себя три электрода: катод К, сетку S и анод А. Батарея Бн обеспечивала регулируемый накал катода, батарея Б1 создавала ускоряющее напряжение U 1 между катодом и сеткой. Батарея Б2 создавала тормозящее напряжение U 2 между сеткой и анодом. Ток через пары ртути между сеткой S и анодом А измерялся гальванометром Г. Процесс измерений сводится к построению вольтамперной характеристики лампы. Постепенно увеличивалось напряжение U 1 между катодом К и сеткой S и записывался ток i по гальванометру Г между сеткой S и анодом А при постоянном задерживающем напряжении Если бы в лампе был вакуум, то вольтамперная характеристика представляла бы собой монотонную кривую, показанную на рис. 7 вверху. При больших напряжениях U 1>> U 2 ток i стремится в вакууме к току насыщения, когда все испускаемые катодом электроны приходят на анод. В парах ртути на вольтамперной кривой появляются впадины, начинающиеся при напряжениях ускоряющего поля U 1 = 4,9; 9,8; 14,7 вольт (рис. 7 внизу). Их можно объяснить так. До напряжения 4,9 В электроны испытывают лишь упругий удар с атомами ртути. Поскольку масса атомов ртути в 400 000 раз больше массы электронов, а тепловая скорость атомов ртути по сравнению со скоростью электронов пренебрежимо мала, то электроны сталкиваются с атомами как с неподвижной стенкой. Скорость электронов меняется лишь по направлению, но не по величине. При U 1 > U 2 кинетическая энергия электронов eU 1 оказывается достаточной для преодоления задерживающего поля U 2. С увеличением U 1 всё большая часть испущенных катодом электронов попадает на анод. Ток растёт. Но вот при напряжении 4,9 В энергия электронов оказывается равной тому кванту энергия атома ртути, который необходим для перехода атома из одного стационарного состояния в другое. При этом напряжении возле сетки S возникает зона неупругих столкновений электронов с атомами. Электроны гасят свою скорость у самой сетки S и потому не могут пройти на анод А из-за тормозящего поля U 2. Возникает первый спад тока i. С дальнейшим ростом U 1 зона неупругих столкновений постепенно перемещается влево. Она оказывается посредине между катодом К и сеткой S при напряжении 9,8 В. Затормозившиеся здесь электроны вновь успевают разогнаться до энергии 4,9 эВ, у сетки S появляется вторая зона неупругих столкновений, и на кривой i (U 1) появляется второй спад. Третий спад на кривой появляется при напряжении 14,7 В, когда у сетки S появляется третья зона неупругих столкновений. Из результатов опытов следовало, что атомы ртути поглощают лишь строго определённую порцию энергии, равную e Δ U 1 = 4,9 эВ. Поглотив эту энергию, атомы ртути должны перейти на более высокий энергетический уровень, иначе, должны возбудиться. Рано или поздно, возвращаясь в основное (не возбуждённое) состояние, атомы ртути должны сбрасывать эту энергию в виде кванта hν ЭМ волны. Фотографирование спектра излучения паров Hg показало, что при напряжении U 1 > 4,9 В пары Hg действительно излучают УФ волну с λ = 253,7 нм. Если верны постулаты Бора, то энергия излучаемых фотонов hν равна энергии электронов при резонансном поглощении.
4. Боровская теория водородоподобного атома. Рассмотрим основные параметры атома, построенного в соответствии с постулатами Бора. Будем говорить в общем случае о водородоподобном атоме, имеющем ядро с зарядом ze +, вокруг которого движется один электрон. Это, например, атом водорода, z = 1; однократно ионизированный атом гелия (ион гелия He +), z = 2; двукратно ионизированный атом лития (ион лития Li ++), z = 3 и т.д. В соответствии с результатами опытов Резерфорда полагаем, что взаимодействие электрона с ядром подчиняется закону Кулона. Электрон в атоме Бора движется вокруг ядра под действием кулоновских сил. В первом приближении можно считать, что масса ядра бесконечно велика по сравнению с массой электрона. В этом случае ядро остаётся неподвижным, а электрон движется по круговым орбитам. Уравнение его движения можно записать так:
Здесь Используя условие квантования момента импульса круговых орбит из первого постулата Бора получаем систему двух уравнений, содержащую теорию атома.
а. Радиусы разрешённых уровней энергии найдём, исключив из системы уравнений (2.5) и (2.6) скорость движения электрона v. Из второго уравнения
Здесь rn – радиус n- й орбиты, где n = 1, 2, 3, … Число n называют главным квантовым числом. При z = 1 и n = 1 получаем радиус самого низкого энергетического уровня атома водорода (боровский радиус)
Диаметр атома водорода в основном состоянии равен В атомной физике широко используется внесистемная единица длины ангстрём ( Для других водородоподобных ядер формулу для rn удобно записывать так:
Итак, радиусы rn разрешённых уровней в водородоподобных атомах растут по квадратичному закону с ростом номера n. В разных атомах они тем меньше, чем больше номер элемента z в таблице Менделеева. б. Скорость движения электронов на разрешённых уровнях найдём, подставив rn из формулы (2.7) в уравнение (2.6).
Чем выше уровень, тем меньше на нём скорость движения электрона. На первом боровском уровне атома водорода скорость электрона составляет На втором боровском уровне, n = 2, скорость в 2 раза меньше, в. Энергия атома на разрешённых уровнях слагается из кинетической энергии электрона Ek и потенциальной энергии En взаимодействия электрона с ядром. Кинетическую энергию можно выразить из уравнения движения (2.5). Потенциальная энергия электрона в кулоновском поле ядра
Здесь Отсюда находится полная энергия атома.
Подставив сюда rn из (2.7), получаем:
Здесь me – масса электрона, n = 1, 2, 3, … – квантовое число. Электрон притягивается к ядру, поэтому полная энергия системы ядро-электрон отрицательна. С ростом n энергия атома, уменьшаясь по абсолютной величине, растёт. При Для графического отображения энергетических уровней атома обычно откладывают по вертикальной оси значения энергии En, отмечая их отрезками горизонтальных прямых. Система стационарных уровней атома на тонкой схеме принимает вид, показанный на рис. 8. Низший уровень (n = 1) с минимальным значением энергии атома является самым устойчивым. Это основное состояние атома. Для перехода атома на уровни n = 2, 3, 4, … атом должен получить извне соответствующую порцию энергии. Поэтому состояния с 5. Излучение атома водорода. Рассмотрим, как объясняет теория Бора сериальные закономерности в спектре атома водорода. Схема на рис.8 делает механизм излучения атома наглядным. Чтобы испускать квант энергии hν, электрон в атоме должен перейти с более высокого уровня на низкий. Для краткости говорят атом переходит с одного уровня на другой. При переходе атома водорода (z = 1) из состояния m в состояние n излучается фотон с энергией
Разделив на hc, получаем формулу Бальмера.
Если теоретические построения в теории Бора справедливы, то коэффициент перед скобками должен быть равен постоянной Ридберга. Из спектрологии (опыт) Вычисленное из (2.15) Совпадение R, вычисленного в теории, с опытом с точностью до 4-х знаков можно считать большим успехом теории Бора. Из энергетической диаграммы, показанной на рис.9, становится понятным механизм появления спектральных серий. УФ серия Лаймана появляется при переходах атома водорода из любых возбуждённых состояний на низший энергетический уровень с n = 1. Здесь могут быть самые большие энергетические ступени, и потому самые малые длины волн λ. Серия Бальмера образуется при переходе возбуждённого атома на уровень n = 2. Энергетические ступени здесь уже меньше, поэтому серия Бальмера попадает в видимый диапазон. Энергетические ступени в сериях Пашена, Брэкета и Пфунда становятся ещё меньше. Поэтому каждая последующая серия уходит всё дальше в ИК диапазон. 6. Потенциалы возбуждения атома водорода – это те напряжения U электрического поля, в котором должен разогнаться электрон, чтобы его энергия оказалась равной кванту энергии, поглощаемой или излучаемой атомом.
Поскольку невозбуждённое состояние атома соответствует n = 1, то все потенциалы возбуждения вычисляются из формулы Бальмера для серии Лаймана. Выразив 1/ l из (1.2) и подставив в (2.16), получаем:
При n = 2 получаем 1-й потенциал возбуждения атома водорода.
При n = ¥ получается такой квант энергии, при поглощении которого электрон уходит из атома. Атом превращается в ион. Потенциал ионизации атома водорода U ¥ = 13,6 В. 7. Магнитный момент электрона. Электрон – электрически заряженная частица. Поэтому наряду с механическим моментом Магнитный момент М кругового тока M = iS, где i – ток, протекающий по замкнутому витку, а S – площадь витка. Циркулирующий по круговой орбите электрон создаёт ток i = en = ev/ 2 pr, где n – частота обращения электрона. Выразив скорость v орбитального движения электрона через механический момент импульса L, v = L/mer, и подставив, получаем: i = ev/ 2 pr = eL/2mepr. Площадь «витка» S = pr 2, где r – радиус орбиты. Отсюда орбитальный магнитный момент электрона
При n = 1 получаем минимальный магнитный момент электрона в атоме водорода в основном состоянии: 8. Принцип соответствия. В 1923 г. Нильс Бор сформулировал постулат, названный им принципом соответствия. Суть его в том, что устанавливается количественный критерий, позволяющий решать, каким законам – квантовым или классическим – подчиняется в данном явлении система. Например, электрон в атоме в рамках классической ЭМ теории должен падать с верхних энергетических уровней на нижние непрерывно. В квантовой теории электрон переходит скачками, причём с увеличением квантового числа n величина энергетических скачков постепенно уменьшается. В результате при больших n изменение энергии электрона в атоме будет происходить практически непрерывно, а само явление можно рассматривать в рамках классической физики. Количественным критерием, по Бору, является величина J, называемая действием. Действие вычисляется как интеграл по замкнутой траектории в фазовом пространстве координаты – импульса.
Здесь p – обобщённый импульс, q – обобщённая координата. Если J» h, то явление подчиняется квантовым закономерностям. Если J >> h, то явление можно описывать в рамках классических законов. Постоянную Планка h называют квантом действия. Принцип соответствия понимают часто в более широком смысле. Любая новая теория, претендующая на более глубокое описание физической реальности и на более широкую область применимости, чем старая, должна включать старую теорию как предельный случай. Например, релятивистская механика включает в себя механику Ньютона как предельный случай малых скоростей, когда (v/c) → 0, оптика включает в себя геометрическую как предел при (λ/a) → 0, где λ – длина волны света, a – характерный размер препятствия. 9. Достоинства теории Бора. Модель Бора была крупным шагом в развитии теории строения атома. Её достоинства: а. Объяснила сериальные закономерности в спектрах атома водорода. Вычисленная на её основе постоянная Ридберга для водорода с точностью до 4-х знаков совпадает с опытным значением. Это совпадение оказывается ещё лучше, если в уравнении движения электрона учесть, что электрон движется не вокруг геометрического центра ядра, а вместе с ядром движется вокруг общего центра масс. б. Объяснила сериальные закономерности в спектрах водородных атомов. Ещё в 1897 г. американский астроном Эдвард Пикеринг обнаружил в спектрах некоторых звёзд серию, напоминающую серию Бальмера, но немного смещённую в фиолетовую область спектра. Число линий в серии Пикеринга было больше, чем в серии Бальмера. Избыточные линии соответствовали дробным значениям числа n и не поддавались никаким объяснениям. Применение теории Бора показало, что серия Пикеринга принадлежит излучению однократно ионизированных атомов гелия и определяется формулой:
Смещение линий в фиолетовую область объяснилось тем, что постоянные Ридберга для гелия и водорода несколько отличаются из-за различия в массах ядер атомов. Исследование спектров двукратно ионизированного лития Li ++ и трёхкратно ионизированного бериллия Be +++ показали, что и для них применима обобщённая формула Бальмера, а все сдвиги спектров объяснялись теорией Бора. в. Успехи теории Бора в объяснении спектра водородных и водородоподобных атомов показали, что классическая физика неприменима к описанию внутриатомных процессов. Теория Бора явилась толчком к большому числу экспериментальных работ, давших много важных результатов. 10. Недостатки теории Бора. Главные из них: а. Не позволяет определять интенсивность спектральных линий. Известно, что линии в спектрах имеют разную яркость. Очевидно, дело в том, что одни энергетические переходы в атомах совершаются относительно чаще, другие – реже. В результате в излучение одной спектральной линии
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 401; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.36.45 (0.015 с.) |

 . Формула Бальмера, 1885 (1.1)
. Формула Бальмера, 1885 (1.1)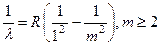 . Серия Лаймана, 1906 (1.2)
. Серия Лаймана, 1906 (1.2) . Серия Пашена, 1908 (1.3)
. Серия Пашена, 1908 (1.3) . Серия Брэккета, 1922 (1.4)
. Серия Брэккета, 1922 (1.4) . Серия Пфунда, 1924 (1.5)
. Серия Пфунда, 1924 (1.5) Обобщённая формула Бальмера (1.6)
Обобщённая формула Бальмера (1.6) (1.7)
(1.7) – заряд шаровой области радиуса r £ R,
– заряд шаровой области радиуса r £ R, .
. , а me – масса электрона.
, а me – масса электрона. . Ускоренно движущийся электрон излучает электромагнитную волну той же частоты ω 0.
. Ускоренно движущийся электрон излучает электромагнитную волну той же частоты ω 0. , (1.8)
, (1.8) . (1.9)
. (1.9) м) меньше радиуса орбиты Земли (
м) меньше радиуса орбиты Земли ( м) всего лишь в 210 раз!
м) всего лишь в 210 раз! атомов. (1.10)
атомов. (1.10) . (1.11)
. (1.11) (1.12)
(1.12)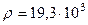 кг/м3. Отсюда радиус атома
кг/м3. Отсюда радиус атома  м.
м. (1.13)
(1.13) м.
м. (1.14)
(1.14) (1.15)
(1.15) (1.16)
(1.16)
 (1.17)
(1.17) м/с. Это вполне классическая скорость, равная 0,7% от скорости света в вакууме.
м/с. Это вполне классическая скорость, равная 0,7% от скорости света в вакууме. (1.18)
(1.18) м/с2. По меркам микрофизики это гигантская величина. Электрический заряд, испытывающий ускорение, по законам классической электродинамики излучает электромагнитную волну. Энергия ЭМ волны может черпаться лишь из энергии электрона. Но это значит, что радиус орбиты электрона должен постепенно уменьшаться.
м/с2. По меркам микрофизики это гигантская величина. Электрический заряд, испытывающий ускорение, по законам классической электродинамики излучает электромагнитную волну. Энергия ЭМ волны может черпаться лишь из энергии электрона. Но это значит, что радиус орбиты электрона должен постепенно уменьшаться. с. Спустя это время электрон должен упасть на ядро, а атом должен превратиться в какой-то другой объект материи.
с. Спустя это время электрон должен упасть на ядро, а атом должен превратиться в какой-то другой объект материи. Правило квантования орбит (2.1)
Правило квантования орбит (2.1) Правило частот Бора (2.2)
Правило частот Бора (2.2) (2.3)
(2.3) В.
В.
 Дж. Разделив это число на заряд электрона
Дж. Разделив это число на заряд электрона  Кл, получаем энергию фотона в электронвольтах,
Кл, получаем энергию фотона в электронвольтах,  эВ. Это как раз энергия электронов e Δ U 1 при резонансном поглощении.
эВ. Это как раз энергия электронов e Δ U 1 при резонансном поглощении. или
или  (2.4)
(2.4) k – радиус орбиты электрона, me – масса покоя электрона.
k – радиус орбиты электрона, me – масса покоя электрона. (2.5)
(2.5) где
где  Подставляем в первое уравнение.
Подставляем в первое уравнение. (2.7)
(2.7) м.
м. м.
м.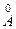 ),
),  Один ангстрём равен приблизительно поперечнику атома водорода в основном состоянии.
Один ангстрём равен приблизительно поперечнику атома водорода в основном состоянии. (2.8)
(2.8) (2.9)
(2.9) м/с, что совпадает со значением, вычисленном на с.
м/с, что совпадает со значением, вычисленном на с. м/с, на третьем, n = 3, скорость в 3 раза меньше и т.д.
м/с, на третьем, n = 3, скорость в 3 раза меньше и т.д. (2.10)
(2.10) (2.11)
(2.11) где e – – заряд электрона, отрицательное число.
где e – – заряд электрона, отрицательное число. (2.12)
(2.12) (2.13)
(2.13)
 из области отрицательных значений.
из области отрицательных значений. называют возбуждёнными.
называют возбуждёнными. (2.14)
(2.14) (2.15)
(2.15) м–1.
м–1. м–1.
м–1. (2.16)
(2.16)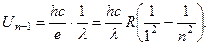 (2.17)
(2.17) При n = 3 получаем 2-й потенциал возбуждения атома водорода U 2 = 12,12 В. Подставляя n = 4, 5, 6, и т.д., можно вычислить все последующие потенциалы возбуждения U 3 = 12,79 В, U 4 = 13,09 В…
При n = 3 получаем 2-й потенциал возбуждения атома водорода U 2 = 12,12 В. Подставляя n = 4, 5, 6, и т.д., можно вычислить все последующие потенциалы возбуждения U 3 = 12,79 В, U 4 = 13,09 В… электрон в атоме обладает орбитальным магнитным моментом.
электрон в атоме обладает орбитальным магнитным моментом. (2.18)
(2.18) Дж/Тл. Его называют магнетон Бора.
Дж/Тл. Его называют магнетон Бора. (2.19)
(2.19) где m = 5, 6, 7, … Серия Пикеринга (2.20)
где m = 5, 6, 7, … Серия Пикеринга (2.20)


