
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физика атома, твёрдого тела и атомного ядраСтр 1 из 11Следующая ⇒
Физика атома, твёрдого тела и атомного ядра Литература 1. Сивухин Д.В. Общий курс физики. Атомная и ядерная физика. Часть 1. Учебное пособие для студентов вузов. – М.: Наука, 1986. – 416 с. 2. Сивухин Д.В. Общий курс физики. Атомная и ядерная физика. Часть 2. Учебное пособие для студентов вузов. – М.: Наука, 1989. – 415 с. 3. Шпольский Э.В. Атомная физика. Т1. Учебное пособие для студентов вузов. – М.: Наука, 1974. – 575 с. 4. Шпольский Э.В. Атомная физика. Т2. Учебное пособие для студентов вузов. – М.: Наука, 1974. – 447 с. 5. Савельев И.В. Курс физики. Тома 2 и 3. Учебное пособие для студентов вузов. – М.: Наука, 1989. 6. Калашников С.Г. Электричество. Учебное пособие для студентов вузов. – М.: Наука, 1977. – 591 с. Глава 1. Физика атома Атом Бора 1. Постулаты Бора. Принципиальный отказ от механической трактовки атома сделал датский физик Нильс Бор в 1913 г, когда он сформулировал два постулата. Постулат 1. Правило квантования орбит. Электроны в атоме могут находиться не на любых энергетических уровнях, допускаемых классической механикой. Они могут находиться лишь на определённых стационарных уровнях, на которых орбитальный момент импульса электрона L = mvr кратен величине h/ 2 π.
Атом в стационарном состоянии не излучает и не поглощает энергии. Постулат 2. Правило частот. Переход электрона с одного уровня на другой сопровождается излучением или поглощением кванта энергии
Здесь Ek и Ei – энергия атома с электроном на k -том и i -том уровнях, νik – частота излучаемого или поглощаемого света при переходе электрона с одного уровня на другой. 2. Основания постулатов лежат в опытных фактах. Первый постулат, признающий существование в атомах стационарных энергетических уровней электронов, представляет собой опытный закон природы. Поскольку атомы длительное время существуют, то существуют и их состояния, в которых атомы не излучают и не поглощают. То, что классическая электродинамика не может объяснить этот факт, следует рассматривать как ограниченность электродинамики, не применимость её законов для описания внутриатомных процессов. Основанием второго постулата являются фотоэффект, тепловое излучение и сериальные закономерности в спектре атома водорода. При фотоэффекте свет поглощается квантами hν. Из законов теплового излучения следует, что излучается свет также квантами hν. Но это значит, что и спектральные линии в излучении атома водорода формируются квантами с энергией hν. Если умножить формулу Бальмера (1.6) на hc, где с – скорость света в вакууме, то получаем:
Слева стоит энергия hν кванта излучаемого атомом света, а справа – разность каких-то двух величин с размерностью энергии. Можно предположить, что выражение Rhc/π 2, где n = 1, 2, 3, 4, …, пропорционально энергии атома водорода в стационарных состояниях. В качестве обоснования условия квантования момента импульса электронов на стационарных уровнях в виде L = nh/ 2 π отметим лишь, что именно при таком квантовании из теории Бора вытекает формула Бальмера. 3. Опыты Франка и Герца. Основное положение Бора о дискретности значений энергии атома доказали экспериментально немцы Джеймс Франк и Густав Герц в 1913-14 и 1919-20 годах. Их установка представляла собой эвакуированную лампу с внесённой в неё каплей ртути (рис. 6). Лампа помещалась в печь. Изменяя температуру в печи, можно было менять давление ртутных паров в лампе. В большинстве опытов давление составляло от 1 до 30 мм Hg. Лампа включала в себя три электрода: катод К, сетку S и анод А. Батарея Бн обеспечивала регулируемый накал катода, батарея Б1 создавала ускоряющее напряжение U 1 между катодом и сеткой. Батарея Б2 создавала тормозящее напряжение U 2 между сеткой и анодом. Ток через пары ртути между сеткой S и анодом А измерялся гальванометром Г. Процесс измерений сводится к построению вольтамперной характеристики лампы. Постепенно увеличивалось напряжение U 1 между катодом К и сеткой S и записывался ток i по гальванометру Г между сеткой S и анодом А при постоянном задерживающем напряжении Если бы в лампе был вакуум, то вольтамперная характеристика представляла бы собой монотонную кривую, показанную на рис. 7 вверху. При больших напряжениях U 1>> U 2 ток i стремится в вакууме к току насыщения, когда все испускаемые катодом электроны приходят на анод. В парах ртути на вольтамперной кривой появляются впадины, начинающиеся при напряжениях ускоряющего поля U 1 = 4,9; 9,8; 14,7 вольт (рис. 7 внизу). Их можно объяснить так.
До напряжения 4,9 В электроны испытывают лишь упругий удар с атомами ртути. Поскольку масса атомов ртути в 400 000 раз больше массы электронов, а тепловая скорость атомов ртути по сравнению со скоростью электронов пренебрежимо мала, то электроны сталкиваются с атомами как с неподвижной стенкой. Скорость электронов меняется лишь по направлению, но не по величине. При U 1 > U 2 кинетическая энергия электронов eU 1 оказывается достаточной для преодоления задерживающего поля U 2. С увеличением U 1 всё большая часть испущенных катодом электронов попадает на анод. Ток растёт. Но вот при напряжении 4,9 В энергия электронов оказывается равной тому кванту энергия атома ртути, который необходим для перехода атома из одного стационарного состояния в другое. При этом напряжении возле сетки S возникает зона неупругих столкновений электронов с атомами. Электроны гасят свою скорость у самой сетки S и потому не могут пройти на анод А из-за тормозящего поля U 2. Возникает первый спад тока i. С дальнейшим ростом U 1 зона неупругих столкновений постепенно перемещается влево. Она оказывается посредине между катодом К и сеткой S при напряжении 9,8 В. Затормозившиеся здесь электроны вновь успевают разогнаться до энергии 4,9 эВ, у сетки S появляется вторая зона неупругих столкновений, и на кривой i (U 1) появляется второй спад. Третий спад на кривой появляется при напряжении 14,7 В, когда у сетки S появляется третья зона неупругих столкновений. Из результатов опытов следовало, что атомы ртути поглощают лишь строго определённую порцию энергии, равную e Δ U 1 = 4,9 эВ. Поглотив эту энергию, атомы ртути должны перейти на более высокий энергетический уровень, иначе, должны возбудиться. Рано или поздно, возвращаясь в основное (не возбуждённое) состояние, атомы ртути должны сбрасывать эту энергию в виде кванта hν ЭМ волны. Фотографирование спектра излучения паров Hg показало, что при напряжении U 1 > 4,9 В пары Hg действительно излучают УФ волну с λ = 253,7 нм. Если верны постулаты Бора, то энергия излучаемых фотонов hν равна энергии электронов при резонансном поглощении.
4. Боровская теория водородоподобного атома. Рассмотрим основные параметры атома, построенного в соответствии с постулатами Бора. Будем говорить в общем случае о водородоподобном атоме, имеющем ядро с зарядом ze +, вокруг которого движется один электрон. Это, например, атом водорода, z = 1; однократно ионизированный атом гелия (ион гелия He +), z = 2; двукратно ионизированный атом лития (ион лития Li ++), z = 3 и т.д. В соответствии с результатами опытов Резерфорда полагаем, что взаимодействие электрона с ядром подчиняется закону Кулона. Электрон в атоме Бора движется вокруг ядра под действием кулоновских сил. В первом приближении можно считать, что масса ядра бесконечно велика по сравнению с массой электрона. В этом случае ядро остаётся неподвижным, а электрон движется по круговым орбитам. Уравнение его движения можно записать так:
Здесь Используя условие квантования момента импульса круговых орбит из первого постулата Бора получаем систему двух уравнений, содержащую теорию атома.
а. Радиусы разрешённых уровней энергии найдём, исключив из системы уравнений (2.5) и (2.6) скорость движения электрона v. Из второго уравнения
Здесь rn – радиус n- й орбиты, где n = 1, 2, 3, … Число n называют главным квантовым числом. При z = 1 и n = 1 получаем радиус самого низкого энергетического уровня атома водорода (боровский радиус)
Диаметр атома водорода в основном состоянии равен В атомной физике широко используется внесистемная единица длины ангстрём ( Для других водородоподобных ядер формулу для rn удобно записывать так:
Итак, радиусы rn разрешённых уровней в водородоподобных атомах растут по квадратичному закону с ростом номера n. В разных атомах они тем меньше, чем больше номер элемента z в таблице Менделеева. б. Скорость движения электронов на разрешённых уровнях найдём, подставив rn из формулы (2.7) в уравнение (2.6).
Чем выше уровень, тем меньше на нём скорость движения электрона. На первом боровском уровне атома водорода скорость электрона составляет На втором боровском уровне, n = 2, скорость в 2 раза меньше, в. Энергия атома на разрешённых уровнях слагается из кинетической энергии электрона Ek и потенциальной энергии En взаимодействия электрона с ядром. Кинетическую энергию можно выразить из уравнения движения (2.5). Потенциальная энергия электрона в кулоновском поле ядра
Здесь Отсюда находится полная энергия атома.
Подставив сюда rn из (2.7), получаем:
Здесь me – масса электрона, n = 1, 2, 3, … – квантовое число. Электрон притягивается к ядру, поэтому полная энергия системы ядро-электрон отрицательна. С ростом n энергия атома, уменьшаясь по абсолютной величине, растёт. При Для графического отображения энергетических уровней атома обычно откладывают по вертикальной оси значения энергии En, отмечая их отрезками горизонтальных прямых. Система стационарных уровней атома на тонкой схеме принимает вид, показанный на рис. 8.
Низший уровень (n = 1) с минимальным значением энергии атома является самым устойчивым. Это основное состояние атома. Для перехода атома на уровни n = 2, 3, 4, … атом должен получить извне соответствующую порцию энергии. Поэтому состояния с 5. Излучение атома водорода. Рассмотрим, как объясняет теория Бора сериальные закономерности в спектре атома водорода. Схема на рис.8 делает механизм излучения атома наглядным. Чтобы испускать квант энергии hν, электрон в атоме должен перейти с более высокого уровня на низкий. Для краткости говорят атом переходит с одного уровня на другой. При переходе атома водорода (z = 1) из состояния m в состояние n излучается фотон с энергией
Разделив на hc, получаем формулу Бальмера.
Если теоретические построения в теории Бора справедливы, то коэффициент перед скобками должен быть равен постоянной Ридберга. Из спектрологии (опыт) Вычисленное из (2.15) Совпадение R, вычисленного в теории, с опытом с точностью до 4-х знаков можно считать большим успехом теории Бора. Из энергетической диаграммы, показанной на рис.9, становится понятным механизм появления спектральных серий. УФ серия Лаймана появляется при переходах атома водорода из любых возбуждённых состояний на низший энергетический уровень с n = 1. Здесь могут быть самые большие энергетические ступени, и потому самые малые длины волн λ. Серия Бальмера образуется при переходе возбуждённого атома на уровень n = 2. Энергетические ступени здесь уже меньше, поэтому серия Бальмера попадает в видимый диапазон. Энергетические ступени в сериях Пашена, Брэкета и Пфунда становятся ещё меньше. Поэтому каждая последующая серия уходит всё дальше в ИК диапазон. 6. Потенциалы возбуждения атома водорода – это те напряжения U электрического поля, в котором должен разогнаться электрон, чтобы его энергия оказалась равной кванту энергии, поглощаемой или излучаемой атомом.
Поскольку невозбуждённое состояние атома соответствует n = 1, то все потенциалы возбуждения вычисляются из формулы Бальмера для серии Лаймана. Выразив 1/ l из (1.2) и подставив в (2.16), получаем:
При n = 2 получаем 1-й потенциал возбуждения атома водорода.
При n = ¥ получается такой квант энергии, при поглощении которого электрон уходит из атома. Атом превращается в ион. Потенциал ионизации атома водорода U ¥ = 13,6 В. 7. Магнитный момент электрона. Электрон – электрически заряженная частица. Поэтому наряду с механическим моментом Магнитный момент М кругового тока M = iS, где i – ток, протекающий по замкнутому витку, а S – площадь витка. Циркулирующий по круговой орбите электрон создаёт ток i = en = ev/ 2 pr, где n – частота обращения электрона. Выразив скорость v орбитального движения электрона через механический момент импульса L, v = L/mer, и подставив, получаем: i = ev/ 2 pr = eL/2mepr. Площадь «витка» S = pr 2, где r – радиус орбиты. Отсюда орбитальный магнитный момент электрона
При n = 1 получаем минимальный магнитный момент электрона в атоме водорода в основном состоянии: 8. Принцип соответствия. В 1923 г. Нильс Бор сформулировал постулат, названный им принципом соответствия. Суть его в том, что устанавливается количественный критерий, позволяющий решать, каким законам – квантовым или классическим – подчиняется в данном явлении система. Например, электрон в атоме в рамках классической ЭМ теории должен падать с верхних энергетических уровней на нижние непрерывно. В квантовой теории электрон переходит скачками, причём с увеличением квантового числа n величина энергетических скачков постепенно уменьшается. В результате при больших n изменение энергии электрона в атоме будет происходить практически непрерывно, а само явление можно рассматривать в рамках классической физики. Количественным критерием, по Бору, является величина J, называемая действием. Действие вычисляется как интеграл по замкнутой траектории в фазовом пространстве координаты – импульса.
Здесь p – обобщённый импульс, q – обобщённая координата. Если J» h, то явление подчиняется квантовым закономерностям. Если J >> h, то явление можно описывать в рамках классических законов. Постоянную Планка h называют квантом действия. Принцип соответствия понимают часто в более широком смысле. Любая новая теория, претендующая на более глубокое описание физической реальности и на более широкую область применимости, чем старая, должна включать старую теорию как предельный случай. Например, релятивистская механика включает в себя механику Ньютона как предельный случай малых скоростей, когда (v/c) → 0, оптика включает в себя геометрическую как предел при (λ/a) → 0, где λ – длина волны света, a – характерный размер препятствия. 9. Достоинства теории Бора. Модель Бора была крупным шагом в развитии теории строения атома. Её достоинства: а. Объяснила сериальные закономерности в спектрах атома водорода. Вычисленная на её основе постоянная Ридберга для водорода с точностью до 4-х знаков совпадает с опытным значением. Это совпадение оказывается ещё лучше, если в уравнении движения электрона учесть, что электрон движется не вокруг геометрического центра ядра, а вместе с ядром движется вокруг общего центра масс. б. Объяснила сериальные закономерности в спектрах водородных атомов. Ещё в 1897 г. американский астроном Эдвард Пикеринг обнаружил в спектрах некоторых звёзд серию, напоминающую серию Бальмера, но немного смещённую в фиолетовую область спектра. Число линий в серии Пикеринга было больше, чем в серии Бальмера. Избыточные линии соответствовали дробным значениям числа n и не поддавались никаким объяснениям. Применение теории Бора показало, что серия Пикеринга принадлежит излучению однократно ионизированных атомов гелия и определяется формулой:
Смещение линий в фиолетовую область объяснилось тем, что постоянные Ридберга для гелия и водорода несколько отличаются из-за различия в массах ядер атомов. Исследование спектров двукратно ионизированного лития Li ++ и трёхкратно ионизированного бериллия Be +++ показали, что и для них применима обобщённая формула Бальмера, а все сдвиги спектров объяснялись теорией Бора. в. Успехи теории Бора в объяснении спектра водородных и водородоподобных атомов показали, что классическая физика неприменима к описанию внутриатомных процессов. Теория Бора явилась толчком к большому числу экспериментальных работ, давших много важных результатов. 10. Недостатки теории Бора. Главные из них: а. Не позволяет определять интенсивность спектральных линий. Известно, что линии в спектрах имеют разную яркость. Очевидно, дело в том, что одни энергетические переходы в атомах совершаются относительно чаще, другие – реже. В результате в излучение одной спектральной линии уходит больше фотонов в излучение, другой – меньше. Но почему это происходит, теория Бора не даёт объяснения. В её рамках нет даже базы для постановки такого вопроса. б. Теория Бора не работает в атомах, следующих за водородом. Нет механизма формирования структуры атомов в таблице Менделеева. Теория Бора не объясняет природу химических связей. Не позволяет объяснить спектры многоэлектронных атомов. в. теория Бора логически противоречива. Она не является ни классической, ни квантовой. В системе двух уравнений, лежащих в её основе, одно – уравнение движения электрона – классическое, другое – условие квантования орбит – квантовое. Но исторически теория Бора сыграл исключительно важную роль. Она явилась переходным этапом от классической к последовательно квантовой теории. Уравнение Шрёдингера 1. Уравнение Шрёдингера. В 1925 г. австрийский физик Эрван Шрёдингер, основываясь на общих соображениях, сконструировал дифференциальное уравнение для волновой функции Де Бройля (подробнее см. [1], с.с. 137-178).
Здесь Для систем в стационарном состоянии, когда все наблюдаемые физические параметры не меняются с течением времени, уравнение Шрёдингера имеет вид:
Здесь E – полная энергия системы. В случае стационарного поля она остаётся постоянной. Уравнение Шрёдингера является основным уравнением нерелятивистской квантовой механики. Его справедливость доказывается тем, что все вытекающие из него следствия очень хорошо согласуются с ответом. Поэтому до настоящего времени уравнение Шрёдингера вызывает у некоторых физиков чувство полумистического восхищения. 2. Вероятностный смысл функции Ψ. В том же 1926 г. немец Макс Борн показал, что функция Ψ имеет вероятностный смысл. Квадрат модуля волновой функции
Из вероятностного смысла волновой функции Ψ следует, что квантовая механика имеет статистический характер. Она не позволяет определить положение частицы в пространстве или определить траекторию её движения. В рамках квантовой механики ставить вопрос о точном местонахождении частицы или о траектории её движения некорректно. С помощью волновой функции Ψ можно лишь предсказать, с какой вероятностью частица может быть обнаружена в разных по величине и положению объёмах пространства. 3. Частица в одномерной потенциальной яме. Математический аппарат квантовой механики очень труден. Число задач, в которых уравнение Шрёдингера решается точно, невелико. В большинстве задач решения приближённые. Они изучаются в курсах теоретической физики. Самая простая задача о движении частицы в одномерной потенциальной яме рассматривается здесь для того, чтобы познакомиться с некоторыми понятиями квантовой механики и убедиться в том, что условия квантования энергии заложены в самом уравнении Шрёдингера. Рассмотрим состояние частицы в одномерной бесконечно глубокой прямоугольной потенциальной яме. Это значит, что потенциальная энергия U частицы удовлетворяет условиям:
Здесь l – длина потенциальной ямы вдоль оси ОX. Так как в задаче нет изменяющихся во времени силовых полей, то она соответствует уравнению Шрёдингера для стационарных состояний (4.2). В декартовых координатах, в которых составлена задача, выражение ∆Ψ имеет вид:
Задача одномерная, члены, содержащие переменные y и z, выпадают. Уравнение (4.2) упрощается. (Напомним, что в яме U = 0).
Покажем, что стенки ямы непроницаемы для частицы. Выйти за пределы ямы она не может. Отсюда следуют граничные условия для волновой функции Ψ.
Обозначим коэффициент
Это уравнение напоминает уравнение движения незатухающего гармонического осциллятора. Разница в том, что в осцилляторе независимая переменная – время t. Здесь независимая переменная – координата x. Решение уравнения (4.8) имеет вид:
4. Квантование энергии. Найдём по условиям задачи постоянные интегрирования А и α. Воспользуемся вначале краевыми условиями (4.7).
Из первого условия вытекает Из второго условия также нельзя определить амплитуду А. Но из него вытекает условие квантовой энергии частицы. Действительно,
Условие n = 0 нужно исключить, так как здесь получается Итак, из условия (4.11) следует:
В уравнении Шрёдингера уже заложен дискретный спектр значений энергии частицы Е. Уравнение Шрёдингера (4.8) имеет решение не при любых значениях Е, а лишь при некоторых, определяемых формулой (4.12). Эти избранные значения Е называются собственными значениями параметра, в данном случае, собственными значениями энергии Е. 5. Нормировка волновой функции. Вторая постоянная интегрирования – амплитуда А функции Ψнаходится из условия нормировки. Суть этого условия в том, что достоверно известно, что частица находится в яме. Вероятность P пребывания частицы в яме равна 1.
Так как
Итак, Решение уравнения (4.8) имеет вид:
Значения Ψ, удовлетворяющие уравнению Шрёдингера, называются собственными функциями уравнения Шрёдингера. На рис. 16а слева показан график функции Ψ в яме при разных квантовых числах n = 1, 2, 3, … То, что значения Ψ в каждой точке пространства не меняется во времени (стационарная задача) позволяет толковать её как стоячую волну, образованную сложением бегущей волны (слева направо) с упруго отражённой от стенки x = l (справа налево). При n = 1 наиболее вероятное пребывание частицы в области середины ямы x = l/ 2. При n = 2 обнаружить частицу в центре маловероятно. Зато с одинаковой вероятностью можно найти её вблизи центров x = l/ 4 и x =3 l/ 4 «половинок» ямы. Длина волны λ, характеризующая волну Ψ, найдётся из уравнения: 6. Коплексная форма функции Ψ. Пусть вдоль оси ОХ двигается фотон с энергией
Физически здесь А – напряжённость электрического поля волны. Фазу волны
Волновая функция фотона есть
То, что величина А есть напряжённость электрического поля, для описания волновых свойств фотона не имеет принципиального значения. Выражение (4.18) можно формально применить для описания волновых свойств и других нейтральных частиц – нейтрино, нейтрона... Для описания волновых свойств электрически заряженных частиц в волновую функцию добавляется ещё мнимая часть.
Здесь то Квадрат модуля комплексной функции 7. Ротатор. Квантование момента импульса. Ротатором в квантовой механике называется неизменная вращающаяся система, состоящая из частицы массой m c угловой степенью свободы. То есть полагается, что частица может двигаться по окружности радиуса r со скоростью v. Координатой движения является угол поворота φ. Поскольку система квантовая, то по окружности движения частицы должна распространятся волна Де Бройля. Решение уравнения Шрёдингера для обоснований условий квантования момента импульса ротатора является сложной математической задачей. Поэтому сформулируем здесь основные итоги. В отличие от классической механики в квантовой механике определённые значения одновременно могут иметь только квадрат момента импульса L 2 и одна из проекций момента импульса на координатную ось, например Lz. а. Квадрат момента импульса L 2 принимает дискретный ряд значений,
так называемое азимутальное квантовое число. В зависимости от энергетического уровня число l может принимать значения от 0 до п – 1, где п – главное квантовое число. б. Проекция момента импульса на произвольную ось Z также принимает дискретный ряд значений,
так называемое магнитное квантовое число. в. Проекция момента импульса на произвольную ось Z не может превосходить его модуля Отсюда следует, что максимально возможное значение числа Заметим, что произвольная ось Z задаётся в эксперименте обычно с помощью электрического или магнитного поля. В этом случае в качестве оси Z берут направление силовых линий поля. Неопределённость ориентации момента импульса L квантовой системы не есть лишь свидетельство размытости момента импульса в пустом пространстве. Оно остаётся неопределённым и при наличии внешнего воздействия со стороны поля. Квантовое число m определяет ориентацию момента импульса L относительно Если l увеличить, например l = 2, то модуль L также увеличивается, Заметим, что углы между векторами 8. Принцип причинности в квантовой механике. Классическая механика, описывая движение макротел, создаёт детерминированную, то есть причинно собственную картину мира. Это означает следующее. Пусть имеется система конечного числа материальных точек m 1, m 2, …mi в определённом силовом поле. Известно уравнение движения каждой материальной точки этой системы.
Здесь к – число частиц в системе, Принцип причинности утверждает, что если известны начальные условия этой системы, то есть координаты и импульсы всех материальных точек в некоторый момент времени, то состояние системы определено на любой момент времени как в прошлом, так и в будущем. Положение не меняется, если в систему входят не только материальные точки, но и тела. Нужно лишь, чтобы их механические параметры были известными. Исходя из открытого им принципа неопределённостей, Гейзенберг предположил, что принцип причинности в микромире нарушается. Поскольку нельзя однозначно определить координаты и импульсы микрочастиц в системе, то по мнению Гейзенберга, нельзя и спрогнозировать состояние микросистемы на какой-то момент времени.
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 272; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.83.150 (0.135 с.) |
 Правило квантования орбит (2.1)
Правило квантования орбит (2.1) Правило частот Бора (2.2)
Правило частот Бора (2.2) (2.3)
(2.3) В.
В.
 Дж. Разделив это число на заряд электрона
Дж. Разделив это число на заряд электрона  Кл, получаем энергию фотона в электронвольтах,
Кл, получаем энергию фотона в электронвольтах,  эВ. Это как раз энергия электронов e Δ U 1 при резонансном поглощении.
эВ. Это как раз энергия электронов e Δ U 1 при резонансном поглощении. или
или  (2.4)
(2.4) k – радиус орбиты электрона, me – масса покоя электрона.
k – радиус орбиты электрона, me – масса покоя электрона. (2.5)
(2.5) где
где  Подставляем в первое уравнение.
Подставляем в первое уравнение. (2.7)
(2.7) м.
м. м.
м.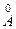 ),
),  Один ангстрём равен приблизительно поперечнику атома водорода в основном состоянии.
Один ангстрём равен приблизительно поперечнику атома водорода в основном состоянии. (2.8)
(2.8) (2.9)
(2.9) м/с, что совпадает со значением, вычисленном на с.
м/с, что совпадает со значением, вычисленном на с. м/с, на третьем, n = 3, скорость в 3 раза меньше и т.д.
м/с, на третьем, n = 3, скорость в 3 раза меньше и т.д. (2.10)
(2.10) (2.11)
(2.11) где e – – заряд электрона, отрицательное число.
где e – – заряд электрона, отрицательное число. (2.12)
(2.12) (2.13)
(2.13)
 из области отрицательных значений.
из области отрицательных значений. называют возбуждёнными.
называют возбуждёнными. (2.14)
(2.14) (2.15)
(2.15) м–1.
м–1. м–1.
м–1. (2.16)
(2.16)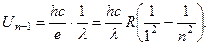 (2.17)
(2.17) При n = 3 получаем 2-й потенциал возбуждения атома водорода U 2 = 12,12 В. Подставляя n = 4, 5, 6, и т.д., можно вычислить все последующие потенциалы возбуждения U 3 = 12,79 В, U 4 = 13,09 В…
При n = 3 получаем 2-й потенциал возбуждения атома водорода U 2 = 12,12 В. Подставляя n = 4, 5, 6, и т.д., можно вычислить все последующие потенциалы возбуждения U 3 = 12,79 В, U 4 = 13,09 В… электрон в атоме обладает орбитальным магнитным моментом.
электрон в атоме обладает орбитальным магнитным моментом. (2.18)
(2.18) Дж/Тл. Его называют магнетон Бора.
Дж/Тл. Его называют магнетон Бора. (2.19)
(2.19) где m = 5, 6, 7, … Серия Пикеринга (2.20)
где m = 5, 6, 7, … Серия Пикеринга (2.20) . Общее уравнение Шрёдингера (4.1)
. Общее уравнение Шрёдингера (4.1) – мнимая единица, ħ=h/2π, m – масса частицы, U – потенциальная энергия частицы, функция координат, t – время, ∆ – оператор Лапласа.
– мнимая единица, ħ=h/2π, m – масса частицы, U – потенциальная энергия частицы, функция координат, t – время, ∆ – оператор Лапласа. . Уравнение Шрёдингера для стационарных состояний (4.2)
. Уравнение Шрёдингера для стационарных состояний (4.2) определяет плотность вероятности p нахождения частицы в точке пространства,
определяет плотность вероятности p нахождения частицы в точке пространства,  . Вероятность P нахождения частицы в объёме пространства V находится интегрированием.
. Вероятность P нахождения частицы в объёме пространства V находится интегрированием.
 (4.3)
(4.3) (4.4)
(4.4) (4.5)
(4.5) или
или  (4.6)
(4.6)
 (4.7)
(4.7) Тогда
Тогда (4.8)
(4.8) (4.9)
(4.9)
 (4.10)
(4.10) (Случай А = 0 приводит к тому, что
(Случай А = 0 приводит к тому, что 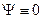 в любой точке ямы. Но это возможно лишь при отсутствии там частицы, что противоречит условию задачи).
в любой точке ямы. Но это возможно лишь при отсутствии там частицы, что противоречит условию задачи). При
При  и
и  отсюда следует:
отсюда следует:
 где n = 1, 2, 3,... (4.11)
где n = 1, 2, 3,... (4.11) А это значит Ψ = 0 при любых x.
А это значит Ψ = 0 при любых x.
 (4.12)
(4.12) (4.13)
(4.13) то
то

 (4.14)
(4.14) (4.15)
(4.15)

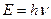 и импульсом
и импульсом 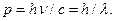 В классическом приближении фотону соответствует электромагнитная волна – бесконечная синусоида.
В классическом приближении фотону соответствует электромагнитная волна – бесконечная синусоида. (4.16)
(4.16) можно представить через энергию и импульс фотона. Так как
можно представить через энергию и импульс фотона. Так как 
 то
то (4.17)
(4.17) (4.18)
(4.18) (4.19)
(4.19) (4.20)
(4.20) (4.21)
(4.21) есть произведение этой функции Ψ на сопряжённую Ψ *.
есть произведение этой функции Ψ на сопряжённую Ψ *. где l = 0, 1, 2, … (4.22)
где l = 0, 1, 2, … (4.22) где m = 0, ±1, ±2, … (4.23)
где m = 0, ±1, ±2, … (4.23) или
или 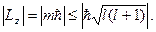 (4.24)
(4.24) как целого числа равно l. Даже при m = l
как целого числа равно l. Даже при m = l  Это обусловлено тем, что направление момента импульса в пространстве является неопределённым.
Это обусловлено тем, что направление момента импульса в пространстве является неопределённым. Это радиус сферы, в которой вписаны три конуса с вершинами в центре сферы. При m = 0 конус вырождается в диск, Lz = 0. При m=+1 получаем конус в верхней части, его высота Lz равна +ћ. При m = – 1 получаем конус в нижней части, его высота Lz = –ћ. То, что известна одна проекция на ось, можно толковать так, что вектор
Это радиус сферы, в которой вписаны три конуса с вершинами в центре сферы. При m = 0 конус вырождается в диск, Lz = 0. При m=+1 получаем конус в верхней части, его высота Lz равна +ћ. При m = – 1 получаем конус в нижней части, его высота Lz = –ћ. То, что известна одна проекция на ось, можно толковать так, что вектор  прецессирует по стенке конуса.
прецессирует по стенке конуса. Радиус сферы стал больше. Но больше стало и число возможных ориентаций вектора
Радиус сферы стал больше. Но больше стало и число возможных ориентаций вектора 
 ...
...  ...
...  (4.25)
(4.25) - суммарная сила, действующая на i -тую частицу.
- суммарная сила, действующая на i -тую частицу.


