Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики нормального закона распределения случайных погрешностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Обработка данных и оценка параметров случайных погрешностей производится методами теории вероятностей и математической статистики. Воспользуемся изложением материала по данной теме, представленной в учебном пособии [3]. Случайные погрешности характеризуются законом распределения. При измерениях размеров наиболее часто это нормальный закон распределения, встречаются также равномерный закон распределения (погрешности размеров в пределах одной группы сортировки при селективной сборке, погрешность обработки во времени из-за износа режущего инструмента), треугольный закон (закон Симпсона) и др. Погрешность результата измерения в общем случае включает систематическую и случайную составляющие (грубая погрешность входит в состав случайной погрешности)
∆Х = ∆Х ст + ∆ Х сл. (5.1)
Составляющая ∆Х ст может носить знаки, как «плюс», так и «минус», при этом, если результат исправляется (вводится поправка) и речь идет о неисключенном остатке систематической погрешности, то перед значением ∆Х ст подразумевается сочетание знаков «±». Составляющая ∆Х сл всегда известна в виде границ с сочетанием знаков «±». Следует понимать, что в общем случае результирующая ∆Х изм не является арифметической суммой составляющих ∆Х ст и ∆Х сл, она состоит из двух данных составляющих, имеющих различные свойства. Задача определения общей погрешности ∆Х общ с учетом составляющих ∆Х ст и ∆Х сл решается вероятностным методом и рассмотрена ниже в разделе 6. В соответствии с законами теории вероятностей, погрешность ∆Х, записанная указанным выражением, также становится случайной величиной, имеющей тот же закон распределения, что и ∆ Х сл. Все сказанное относится и к результату измерения, его на основании приведенных выше выражений можно записать в виде
Х изм = Х дст + ∆Х. (5.2)
Из теории вероятности известно, что закон распределения можно охарактеризовать числовыми характеристиками, которые являются уже неслучайными величинами. Эти характеристики используются для количественной оценки случайной погрешности, среди них основными для погрешности ∆Х, записанной в виде (5.1) являются: - математическое ожидание ∞ М[∆Х] = ∫∆Хр(∆Х)d(∆Х), (5.3) -∞ где р (∆Х) – плотность вероятности погрешности ∆Х; - дисперсия ∞ D [ ∆Х ] = ∫{[ ∆Х – М [ ∆Х ]}2 p (∆Х) d (∆Х). (5.4) -∞
Математическое ожидание погрешности измерений, вычисляемое по формуле (5.3), есть неслучайная величина, она характеризует систематическую составляющую погрешности измерения, т. е. М [ ∆Х изм] = ∆Х ст. Для чисто случайной погрешности, когда ∆Х ст = 0, М [ ∆Х изм] = 0. Дисперсия характеризует степень разброса отдельных значений погрешности относительно М [ ∆Х ] и может служить характеристикой точности проведенных измерений, но имеет размерность измеряемой величины в квадрате. Поэтому в качестве числовой хоарактеристики такого рода для сучайной погрешности чаще используют среднее квадратическое отклонение
σ[ ∆Х ] = √ D [ ∆Х ]. (5.5)
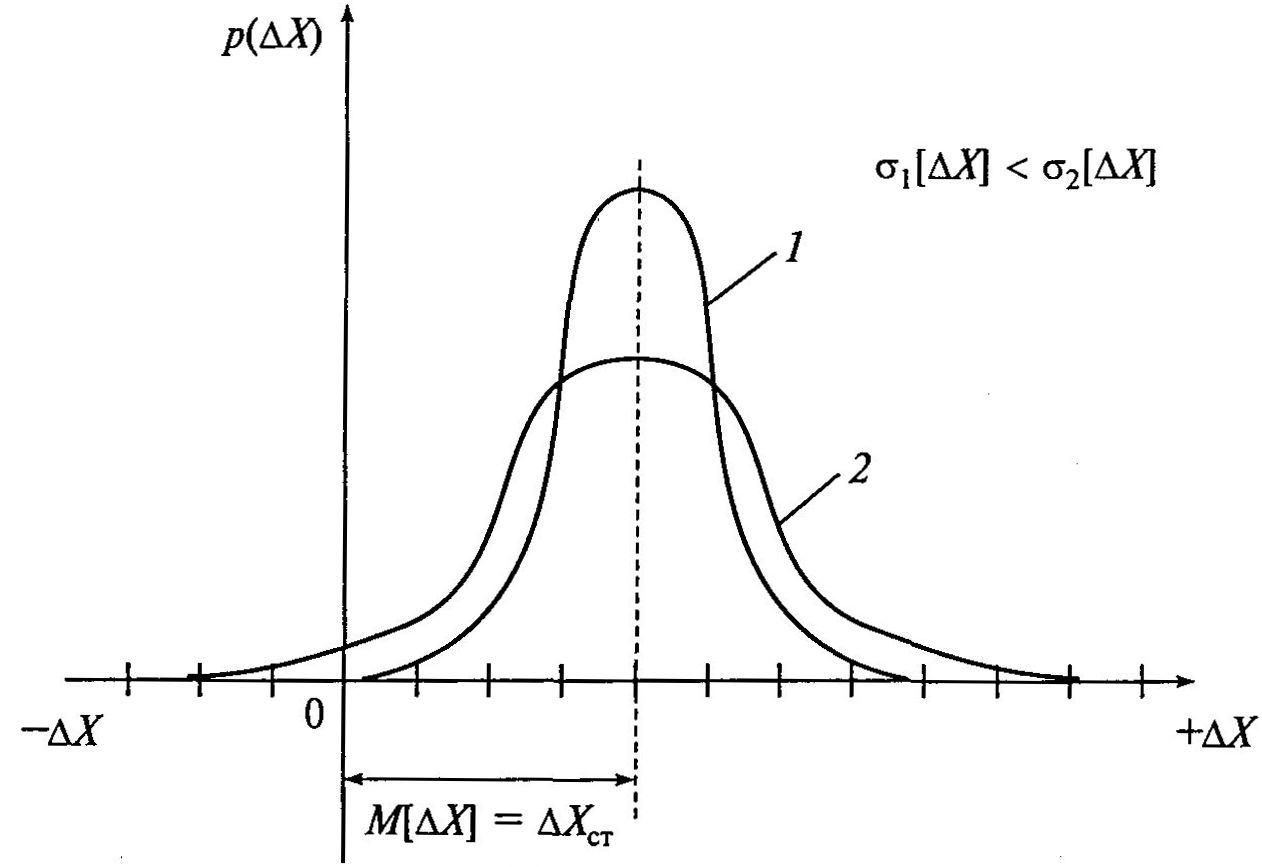
Применительно к погрешностям измерений данную числовую характеристику следует называть средней квадратической погрешностью (СКП) результата измерений. Графическое представление нормального закона распределения случайных погрешностей (дифференциальная функция распределения p (∆Х изм) или плотность вероятностей) приведена на рисунке 5.1, аналитическое выражение этого закона имеет вид
Если характеризовать случайную погрешность безразмерным нормированным числом t = ∆Х / σ [ ∆Х ] (нормировка относительно СКП), то получим кривую нормированного нормального распределения
с аргументом
t = (∆Х – М [ ∆Х ]) / σ[ ∆Х ] (5.8)
Рисунок 5.1 – Кривые дифференциального закона нормального распределения при СКП: σ1 – кривая 1 и σ2 кривая 2 при условии σ1 < σ2
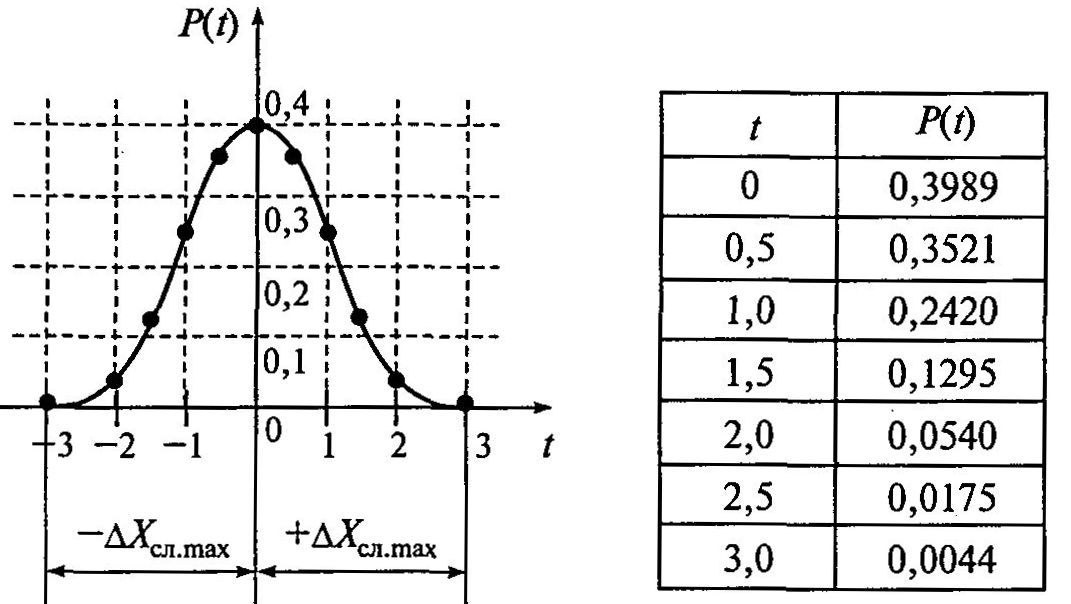
Вид кривой нормированного нормального распределения чисто случайной погрешности (М [ ∆Х ] = 0) приведен на рисунке 5.2.
Рисунок 5.2 – Кривая нормированного закона нормального распределения
Положение кривых нормального распределения относительно начала координат и ее форма определяются соответственно параметрами М [ ∆Х ] и σ[ ∆Х ]. С изменением М [ ∆Х ] форма кривой не изменяется, при полной компенсации статической составляющей погрешности М [ ∆Х ] = 0 и кривая занимает положение, показанное на рисунке 5.2, т. е. симметричное относительно оси ординат. С изменением σ [ ∆Х ] положение кривой не изменяется, с уменьшением этой характеристики кривая становится более вытянутой по отношению к оси ординат, ветви ее сближаются (кривая 1 на рисунке 5.1). По условиям измерительных задач часто необходимо найти максимальную (предельную) случайную погрешность. Эта погрешность связана с СКП и зависит от закона распределения. Для нормального закона, как правило, принимается равной (рисунок 5.2)
∆Х сл.max = ±3 σ [ ∆Х сл]. (5.9)
Для равномерного закона ∆Х сл.max = ±1,73 σ [ ∆Х сл], для треугольного ∆Х сл.max = ±2,45 σ [ ∆Х сл].
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 665; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.253.224 (0.006 с.) |

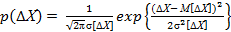 (5.6)
(5.6)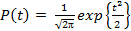 (5.7)
(5.7)