Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Общая методика обучения решению текстовых задачСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Предисловие Пособие написано в соответствии с программой по методике обучения математике в начальной школе и предназначено в первую очередь для студентов очного и заочного отделений факультета начального образования педагогических университетов и институтов. Содержание раздела «Методика обучения решению задач» рассматривается после освоения студентами таких вопросов частной методики как «Методика изучения нумерации чисел», «Методика изучения арифметических действий и формирования вычислительных навыков». Пособие состоит из 4 частей, приложения и включает список рекомендуемой литературы. В первой части сформулированы основные задачи изучения темы и рассмотрены некоторые вопросы, связанные с организацией деятельности студентов в ходе изучения раздела «Методика обучения решению задач». Далее представлено содержание основных тем рассматриваемой части курса методики обучения математике. Для каждой темы приводятся · задания для подготовки к занятию, благодаря которым происходит актуализация у студентов знаний и умений, которые необходимы для успешного изучения содержания раздела «Методика обучения решению задач»; · вопросы для обсуждения, которые помогают студентам выделить наиболее важные моменты каждой темы рассматриваемого раздела; · вопросы и задания для самостоятельной работы, в результате выполнения которых происходит формирование у студентов методико-математических умений, связанных с обучением младших школьников решению текстовых задач; · список рекомендуемой литературы. В третьей части пособия предлагаются дополнительные задания для студентов. Дополнительные задания в большинстве случаев носят исследовательский характер. Они составлены таким образом, чтобы показать студентам возможные направления дальнейших исследований проблемы совершенствования методики обучения младших школьников решению текстовых задач. Круг указанных проблем достаточно широк: от анализа творчества отечественных методистов XIX века, до обсуждения возможностей использования глобальной компьютерной сети Internet в методической деятельности учителя начальных классов. Четвертая часть методических рекомендаций включает варианты для проведения контрольной работы, нацеленной на оценку сформированности у студентов умений, связанных с обучением младших школьников решению арифметических задач. Пособие снабжено приложением, включающим материалы, которые необходимы для выполнения студентами отдельных методико-математических заданий. В частности в Приложениях 1 и 2 представлены выдержки из книги С.И. Шохор-Троцкого «Методика арифметики для учителей начальных школ» (ч. 1. Арифметика изустных вычислений 9-е изд. Москва, 1917 г.), в Приложении 3 цитируются задачи на движение по пособию А. Малинина и К. Буренина «Собрание арифметических задач» (23-е издание, Москва, 1900 г.), в Приложении 4 указаны адреса некоторых интернет-сайтов, на которых обсуждаются проблемы образования.
Организация изучения раздела В результате изучения раздела «Методика обучения решению текстовых задач» студенты должны знать: · содержание стабильной программы по математике для начальных классов и объяснительной записки к ней, касающееся обучения решению задач; · функции и значение текстовых задач в курсе математики начальных классов; · виды задач, рассматриваемых в курсе математики начальной школы; · методы решения текстовых задач; · методические приемы обучения решению задач. Кроме того, у студентов необходимо сформировать следующие базовые методико-математические умения: · целенаправленно использовать различные способы наглядной интерпретации задач; · проводить преобразование задачи с целью реализации развивающей функции обучения; · проводить фронтальный разбор любой задачи курса математики начальных классов; · целенаправленно использовать различные формы записи решения задачи на различных этапах обучения; · использовать различные способы проверки решения задач; · разрабатывать урок обучения решению задач; · подбирать и самостоятельно составлять упражнения, нацеленные на подготовку решения задач различных видов и организовывать деятельность учащихся на подготовительном этапе; · варьировать использование различных методических приемов в зависимости от вида задачи, этапов обучения, подготовки учащихся и других характеристик процесса обучения. Сформированность базовых методико-математических умений является необходимым условием эффективности деятельности будущего учителя при обучении младших школьников решению задач. Однако авторы пособия полагают, что овладение указанными выше умениями есть только первая ступень в направлении профессионального мастерства учителя. Начиная с младших курсов, целесообразно формировать у студентов исследовательские умения, владение которыми позволит выпускникам в дальнейшем совершенствовать и развивать систему своих профессиональных методико-математических умений. Поэтому в настоящее пособие включены задания, которые направлены на формирование у студентов исследовательских умений. В частности, это упражнения, нацеленные на анализ методических текстов, анализ методической деятельности учителя на уроке, составление арифметических задач по заданным сюжетам и математическому содержанию и пр. Указанные задания в большинстве случаев помещены в раздел «Дополнительные задания по методике обучения решению текстовых задач». Среди заданий для самостоятельной работы студентов есть упражнения, в которых демонстрируются использование некоторых методических приемов. Это сделано для того, чтобы студенты, имеющие невысокий уровень методической подготовки, а так же студенты, обучающиеся заочно, имели возможность успешно освоить рассматриваемый раздел курса методики обучения математики. С этой же целью приводится решение одного из вариантов контрольной работы, нацеленной на оценку сформированности у студентов умений, связанных с обучением решению задач. Таким образом, в методических рекомендациях представлены задания различного уровня сложности, что позволяет преподавателю в зависимости от уровня подготовки студентов, специфики очной и заочной форм обучения предлагать для подготовки и обсуждения различный набор заданий. При составлении пособия авторы исходили из того, что необходимо диалогизировать процесс профессиональной методико-математической подготовки студентов. Это достигается при составлении упражнений посредством использования следующих приемов: формулирование упражнений в вопросительной форме, требование от студентов обосновывать свое мнение; постановка проблемных вопросов; формулирование заданий, допускающих различные методические решения и пр. В большинстве современных учебников по методике обучения математике в начальной школе отсутствуют вопросы истории развития методики обучения математики. Методика обучения математике встает перед глазами студентов вне своей истории, вне творчества ученых, которые направляли ее развитие, внесли огромный вклад в становление методов преподавания математики, в формирование содержания школьных математических дисциплин и пр. Поэтому в данное пособие включены задания, предполагающие анализ методических взглядов отечественных педагогов-математиков прошлого, а так же упражнения, в формулировке которых используется историко-методический материал. В пособии предлагаются следующие темы для обсуждения: I. Общая методика обучения решению текстовых задач. II. Методика обучения решению простых задач. III. Методика обучения решению составных задач. IV. Методика обучения решению задач, связанных с пропорционально зависимыми величинами. V. Методика обучения решению задач, связанных с движением. Содержание занятий Задания контрольной работы Задание 1. Описать методику работы над задачей. Тексты задач для задания 1. 1. В банке было 3 л молока, а в бидоне на 6 л больше. Сколько литров молока было в банке и в бидоне вместе? 2. В спортивный лагерь приехали школьники, тренеры и воспитатели, всего 96 человек. Тренеров было 4 человека, воспитателей столько же. Сколько было школьников? 3. В буфет привезли 3 ящика апельсинов, по 9 кг в каждом. Сколько килограммов апельсинов привезли? 4. Для поливки огорода пап принес 16 ведер воды, причем каждый раз он приносил по 2 ведра. Сколько раз ходил папа за водой? 5. На одной грядке посадили рассаду помидоров в 3 ряда, по 8 штук в каждом, а на другой грядке 15 штук. Сколько всего штук рассады посадили на этих двух грядках? 6. В школьной мастерской отремонтировали 40 парт, а столов в 5 раз меньше, чем парт. Сколько всего парт и столов отремонтировали? 7. Для урока труда приготовили 12 листов красной бумаги, зеленой в 2 раза меньше, чем красной, а голубой на 3 листа больше, чем зеленой. Сколько листов голубой бумаги приготовили? 8. Масса двух одинаковых чемоданов равна массе двух одинаковых рюкзаков и сумки. Узнай массу чемодана, если масса рюкзака 8 кг, а масса сумки 4 кг. 9. От Москвы до Ставрополя поезд идет 28 ч, а самолет тратит в 14 раз меньше времени, чем поезд. Сколько часов экономит самолет для пассажира? 10. В прошлом году в заповеднике заготовили на зиму 14 стогов сена для подкормки лосей, а в этом году в 3 раза больше. На сколько больше стогов заготовили в этом году?
Задание 2. Описать методику работы над задачей на пропорциональную зависимость величин. Тексты задач для задания 2. 1. Контролер за 10 минут проверяет 50 деталей. Сколько деталей он проверит за час, если будет проверять по столько же деталей в минуту? 2. В детский сад привезли 10 ящиков яблок, по 9 кг в каждом, и 8 одинаковых по массе ящиков слив. Всего привезли 170 кг фруктов. Сколько килограммов слив было в одном ящике? 3. Два самолета летели с одинаковой скоростью. Один самолет был в воздухе 4 ч, другой – 6 ч. Первый самолет пролетел меньше второго на 1400 км. Какое расстояние пролетел каждый самолет? 4. Два разных автомата выпускают каждый по 30000 спичек в минуту и упаковывают их в коробки: один по 50 штук, другой по 60 штук. Какой автомат упаковывает больше коробков спичек в минуту и насколько коробков больше? 5. В коллекции почтовых марок у мальчика было 24 болгарские и 40 немецких марок. Он поместил их в альбом поровну на каждую страницу. Немецкие марки заняли на 2 страницы больше, чем болгарские. Сколько страниц было занято немецкими марками? 6. Из двух городов, расстояние между которыми 520 км, одновременно вышли навстречу друг другу два поезда и встретились через 4 ч. Один поезд шел со средней скоростью 60 км/ч. С какой средней скоростью шел другой поезд? 7. Расстояние между городом и зимовкой 150 км. Из города к зимовке вышли аэросани со средней скоростью 60 км/ч. В это же время навстречу им из зимовки по той же дороге вышел лыжник со средней скоростью 15 км/ч. На каком расстоянии от зимовки он встретил аэросани? 8. Два лыжника вышли из поселка одновременно и пошли в противоположных направлениях. Один из них шел со средней скоростью 12 км/ч, а другой – 10 км/ч. Через сколько часов расстояние между ними будет 44 км? Какое расстояние пройдет за это время каждый лыжник? 9. В 11 ч с аэродрома вылетели одновременно в противоположных направлениях два самолета. В 14 ч расстояние между ними было 3540 км. Один из них летел со средней скоростью 620 км/ч. С какой средней скоростью летел другой самолет? 10. Из двух городов, расстояние между которыми 960 км, вышли два поезда навстречу друг другу и встретились на середине пути. Первый поезд шел со средней скоростью 60 км/ч, а второй – 80 км/ч. Какой поезд затратил на путь до встречи больше времени и на сколько часов?
Задание 3. Конкретизировать на примере данной задачи методические приемы поиска различных способов решения задачи. Тексты задач для задания 3. 1. Лиза, Аня и Ира вырастили 38 кустиков рассады. Лиза вырастила 13 кустиков, Аня – 14, а остальные вырастила Ира. Сколько кустиков рассады вырастила Ира? 2. На автобазе 37 малых и 29 больших грузовиков. 23 грузовика отправили на стройку. Сколько грузовиков осталось на базе? 3. В коробке лежат красные, синие и зеленые кубики, всего 25 штук. Красных кубиков 12, синих 8, а остальные - зеленые. Сколько зеленых кубиков в коробке? 4. В автобусе было 43 пассажира. На остановке вышли 17 человек. Сколько пассажиров стало в автобусе, если вновь вошли 9 пассажиров? 5. В парке посадили 15 берез и 25 кленов. Все деревья посадили в 5 рядов поровну. Сколько деревьев оказалось в каждом ряду? 6. В теплице расцвели 47 георгинов. 19 из них срезали, но затем распустилось еще 24 георгинов. Сколько георгинов в теплице? 7. Портниха сшила 5 женских и столько же детских платьев. На каждое женское платье она расходовала 3 м ткани, а на каждое детское – 2 м. Сколько ткани израсходовала портниха? 8. В библиотеке на одной полке стояло 32 книги, а на другой 40 книг. 20 книг выдали детям. Сколько книг осталось? 9. Дети в понедельник вскопали 8 грядок, во вторник 7 грядок, и еще им осталось вскопать 9 грядок. Сколько грядок дети должны были вскопать? 10. От куска ситца отрезали двум покупателям по 8 метров, после этого в куске осталось 7 метров ситца. Сколько метров ситца было в куске?
Задание 4. Подобрать и изучить литературу по теме (статьи, книги для учителя, монографии, учебные пособия и пр.), составить аннотации к 3-4 статьям, выделить новые методические приемы работы над задачей, особенности их использования в зависимости от вида задачи и пр. Темы для задания 4. 1. Методика работы над простой задачей. 2. Методика работы над составной задачей. 3. Методика работы над задачей на пропорциональную зависимость величин. 4. Методика работы над задачей на движение. 5. Развитие интереса учащихся в процессе решения задач разных видов. 6. Из истории методики обучения решению текстовых задач в начальной школе. 7. Методика обучения решению текстовых задач в системах развивающего обучения математике. 8. Нестандартные задачи в обучении младших школьников математике. 9. Воспитание младших школьников в процессе обучения решению текстовых задач. 10. Использования моделирования при обучении решению текстовых задач. Таблица вариантов контрольной работы
Образец оформления контрольной работы Обложка тетради: Контрольная работа по методике обучения математике по теме «Методика обучения решению задач» студентки II (III) курса очного (заочного) отделения группы НО-22 факультета начального образования КГПУ им. К.Э. Циолковского Ивановой Марии Петровны Первая страница: Вариант № 11. Задание 1. Описать методику работы над задачей «В магазин привезли 24 кг малины, вишни на 7 кг меньше, чем клубники, а клубники на 10 кг больше, чем малины. Сколько привезли в магазин вишни?». Задание 2. Описать методику работы над задачей «Поезд, следуя из одного города в другой, прошел 180 км пути со скоростью 60 км/ч. На остальной путь ему потребовалось при той же скорости на 4 ч больше. Сколько километров осталось пройти поезду?» Задание 3. Конкретизировать на примере задачи «В связке было 27 красных и 25 синих шаров. 23 шара раздали детям. Сколько шаров осталось в связке?» методические приемы поиска различных способов решения задачи. Задание 4. Подобрать и изучить литературу по теме «Реализация дидактических принципов в процессе обучения младших школьников решению текстовых задач» (статьи, книги для учителя, монографии, учебные пособия и пр.), составить аннотации к 3-4 статьям, выделить новые методические приемы работы над задачей, особенности их использования в зависимости от вида задачи и пр. Каждое задание рекомендуется начинать выполнять со следующей страницы для удобства проверки контрольной работы. Задание 1. Описать методику работы над задачей «В магазин привезли 32 кг малины, вишни на 7 кг меньше, чем клубники, а клубники на 10 кг больше, чем малины. Сколько привезли в магазин вишни?». 1. Подготовка к решению текстовой задачи.
1) Найди места куда приземлятся парашютисты. 2) Реши задачу: «У Сережи 24 марки, а у Феди на 8 марок меньше. Сколько марок у Феди?» 24 – 8 = 16 (м.) 2. Восприятие задачи и ее первичный анализ · О чем говорится в задаче? О ягодах, которые привезли в магазин. · Какие ягоды привезли в магазин? Малину, клубнику и вишню. · Сколько килограммов малины привезли в магазин? 32 кг. · Знаем мы сколько килограммов клубники привезли в магазин? Нет. · Что известно о массе клубники? Что ее привезли на 10 кг больше, чем малины. · Что в задаче сказано о массе вишни? Что ее привезли на 7 кг меньше, чем клубники. Составляем краткую запись. · · Какой главный вопрос задачи? Сколько килограммов вишни привезли в магазин? 3. Поиск решения задачи и составление плана. · · Зная, сколько килограммов малины привезли в магазин и что клубники привезли на 10 кг больше, что мы можем узнать? С колько килограммов клубники привезли в магазин. · Зная сколько привезли клубники и на сколько меньше привезли вишни, что можно найти? Сколько килограммов вишни привезли в магазин. · Каков вопрос задачи? Сколько привезли в магазин вишни? · Что мы узнаем в первом действии? Сколько клубники привезли в магазин. · Каким арифметическим действием мы узнаем, сколько привезли клубники? Сложением. · Что мы найдем во втором действии? Сколько килограммов вишни привезли в магазин. · Каким арифметическим действием мы это узнаем? Вычитанием. 4. Выполнение решения и формулировка ответа. ВозможнЫ следующие варианты записи решения и ответа задачи: · По действиям с вопросами: 1) Сколько килограммов клубники привезли в магазин? 32 + 10 = 42 (кг) 2) Сколько килограммов вишни привезли в магазин? 42 – 7 = 35 (кг) Ответ: 35 кг. · По действиям без пояснения: 1) 32 + 10 = 42 (кг) 2) 42 – 7 = 35 (кг) Ответ: 35 кг вишни привезли в магазин. · По действием с пояснением: 1) 32 + 10 = 42 (кг) клубники привезли в магазин. 2) 42 – 7 = 35 (кг) вишни привезли в магазин Ответ: 35 кг. · Выражением: (32 + 10) – 7 = 35 (кг) Ответ: 35 кг вишни привезли в магазин. 5. Работа над задачей после решения. 1) Выбери правильный ответ. 15, 36, 35, 29, 49. Если учащиеся выбрали числа 15, 29, 49, то они допустили ошибку в выборе действий, если 36 – ошибку в вычислениях. 2) Составление и решение обратной задачи. Учащиеся составляют и решают обратную задачу: «В магазин привезли 35 кг вишни, клубники на 7 г больше, чем вишни, а малины на 10 кг меньше, чем клубники. Сколько привезли в магазин малины?» 35 + 7 = 42 (кг) клубники 42 – 10 = 32 (кг) малины. Ответ: 32 кг малины. Числовые данные, полученные в прямой и обратных задачах, совпадают, значит, ответ найден верно. 3) Решение задачи другими способами. Для того чтобы показать детям решение задачи другим способом можно использовать другую краткую запись условия.
И провести следующую беседу: · Покажите отрезок, который соответствует массе малины. · Покажите отрезок, который соответствует массе клубники. · Покажите отрезок, соответствующий массе вишни. · Покажите отрезок, который показывает, на сколько масса клубники больше, чем малины. · Покажите отрезок, который показывает, на сколько масса вишни меньше, чем масса клубники. · Как мы можем узнать на сколько масса вишни меньше, чем масса клубники? 10 – 7 = 3 (кг) · Как мы можем узнать на сколько масса вишни больше, чем масса малины? 32 + 3 = 35 (кг)
Задание 2. Описать методику работы над следующей задачей: «Поезд, следуя из одного города в другой, прошел 180 км пути со скоростью 60 км/ч. На остальной путь ему потребовалось при той же скорости на 4 ч больше. Сколько километров осталось пройти поезду?» 1. Подготовительный этап. Полезно повторить зависимость между скоростью, временем и расстоянием. С этой целью можно включить в урок следующие задания: · Два велосипедиста движутся с одинаковой скоростью. Первый – 2 часа, второй - 3 часа. Кто из них проедет большее расстояние? · За какое время пешеход, движущийся со скоростью 4 км/ч, пройдет расстояние 12 км? · Какое расстояние за 2 часа проедет лыжник, движущийся со скоростью 7 км/ч. 2. Анализ текста задачи и составление краткой записи условия. · О чём эта задача? О движении поезда. · На какие участки можно разделить путь, пройденный поездом? На путь длинной 180 км и на остальной участок пути. · Что в задаче спрашивается? Сколько километров осталось пройти поезду? · Что в задаче известно? Известна длина первого участка пути – 180 км и скорость поезда – 60 км/ч, известно, что на остальной путь поезд затратил на 4 ч больше. · Что неизвестно? Неизвестно время на первом участке пути, скорость, время и расстояние на втором участке пути. · Что обозначают словосочетание «при той же скорости»? Это означает, что скорость не изменялась. ·
Обозначим на схеме основные величины и их значения.
· Как связаны между собой величины «скорость», «время» и «расстояние»? Чтобы найти скорость, надо расстояние разделить на время, чтобы найти расстояние, надо скорость умножить на время, чтобы найти время, надо расстояние разделить на скорость. · Занесем данные, неизвестные и искомое в таблицу.
3. Разбор задачи. Можно провести аналитический и синтетический способ разбора задачи, приведем оба варианта.
4. Составление плана решения. Учитель предлагает учащимся составить план решения задачи, который выглядит следующим образом:
5. Запись решения и ответа.
Ответ: 420 км. 6. Работа над задачей после решения. После решения задачи необходимо организовать проверку решения задачи. Для этого можно использовать следующие методические приемы: Выбор ответа из предложенных учителем вариантов. 2040 км, 240 км, 420 км, 420 км/ч. Выбор учеником ответа 2040 км говорит об арифметической ошибке; 240 км – об ошибке в выборе действия; 420 км/ч – об ошибке в наименовании. Решение задачи другим способом. 1) 180:60=3 (ч) - время движения поезда на I участке пути. 2) 4+3=7 (ч) - время движения поезда на II участке пути. 3) 7:3=2 (ост.1) – сколько раз время движения на первом участке пути помещается во времени движения на втором участке пути. 4) 180∙2=360 (км) – расстояние, пройденное поездом за 6 часов 5) 360+60=420 (км) - осталось пройти поезду. Установление соответствия между числом, полученным в ответе, и одним из данных в условии. 420:60=7 (ч) время на втором участке пути 7-4=3 (ч) время на первом участке пути 180:3=60(км/ч) скорость на первом участке пути После проверки решения задачи можно изменить одно из данных, например, разницу между временем на различных участках пути. Учащимся предлагается установить, как изменится путь поезда, если на остальной путь поезду потребовалось на 2 ч больше, на 8 ч больше? Можно усложнить условие, например, предположить, что на втором участке пути изменится скорость поезда. Можно задать новый вопрос к задаче: «Сколько км всего прошел поезд».
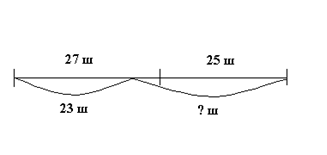
Задание 3. Конкретизировать на примере задачи «В связке было 27 красных и 25 синих шаров. 23 шара раздали детям. Сколько шаров осталось в связке?» методические приемы поиска различных способов решения задачи. В процессе работы над задачей была составлена краткая запись условия и выполнено следующее решение: Было - 27 к. ш. и 25 с.ш. Раздали – 23 ш. Осталось –? ш. 1) 27+25=52 (ш.) было в связке. 2) 52-23=29 (ш.) осталось. Ответ: 29 шариков осталось в связке. Чтобы учащиеся пришли ко второму способу решения задачи, можно использовать различные методические приемы, конкретизируем их применительно к данной задаче. 1. Другой способ разбора задачи. · Мы не знаем шары, какого цвета раздали, предположим, что это были красные шары. Что можно узнать, зная, сколько красных шаров было в связке, и сколько шаров раздали? Сколько красных шаров осталось в связке. · Что можно узнать, зная, сколько красных шаров осталось в связке и сколько синих шаров в связке? Сколько шаров осталось в связке? · Могут ли шары, которые раздали, быть синими? Каким в данном случае будет решение задачи? 2. Анализ выражения, являющегося решением данной задачи. Рассмотрите выражение: (27+25)-23. Какое правило можно использовать при нахождении значения этого выражения? П равило вычитания числа из суммы. Какими способами можно вычесть число из суммы? Что мы узнаем, если из 27 вычтем 23? Сколько в связке осталось шаров красного цвета. Что мы узнаем, если из 25 вычтем 23? Сколько в связке осталось шаров синего цвета. Какими еще способами можно решить эту задачу? II способ: 27-23=4 (ш.) осталось в связке, если бы раздали сначала красные шары. 4+25=29 (ш.) осталось всего. III способ: 25-23=2 (ш.) осталось в связке, если бы раздали сначала синие шары.
2+27=29 (ш.) осталось всего.
3. Использование иной краткой записи и построение другой модели задачи. Сравните схемы, являющиеся краткой записью условия данной задачи. Почему каждая из схем соответствует задаче? 4. Дополнение условия задачи сведениями, позволяющими найти новое решение. Пусть сначала раздали красные шары. Как изменится тогда условие задачи. В связке было 27 красных и 25 синих шаров. 23 красных шара раздали детям. Сколько шаров осталось в связке? Пусть сначала раздали синие шары. Как изменится тогда условие задачи. В связке было 27 красных и 25 синих шаров. 23 синих шара раздали детям. Сколько шаров осталось в связке? 5. Приведение неполного способа решения. В зависимости от уровня подготовки младших школьников можно предложить следующие неполные решения задачи:
1) 27-23=o (ш.) осталось в связке, если бы раздали сначала красные шары. 2) o+25=29 (ш.) осталось всего.
1) o-23=o (ш.) осталось в связке, если бы раздали сначала красные шары. 2) o+o=o (ш.) осталось всего.
1) – 2) + 6. Представление практического разрешения ситуации, описанной в задаче. Предлагается ученикам представить как раздают шары: сначала красные, потом синие.
Задание 4. Подобрать и изучить литературу по теме «Психологические аспекты обучения младших школьников решению текстовых задач» (статьи, книги для учителя, монографии, учебные пособия и пр.), составить аннотации к 3-4 статьям, выделить новые методические приемы работы над задачей, особенности их использования в зависимости от вида задачи и пр. Балл Г.А. О психологическом содержании понятия «задача».// Вопросы психологии. – 1970. - №6. Басангова Р.Б. Познавательная деятельность ученика в ходе решения задач. // Начальная школа. – 2002. - №3. Менчинская Н.А., Моро М.И. Вопросы методики и психологии обучения арифметике в начальных классах. - М.: Просвещение, 1965. Талызина Н.Ф. Формирование познавательной деятельности младших школьников. - М.: Просвещение, 1988. Формирование приемов математического мышления / Под ред. Н.Ф. Талызиной. - М.: Вента-Граф, 1995. Фридман Л.М. Логико-психологический анализ школьных учебных задач. – М.: Педагогика, 1977. В статье Р.Б. Басанговой арифметическая задача рассматривается как стимул познавательной деятельности младших школьников. Автор подробно останавливается на логических и психологических особенностях метода обратных задач. В статье называются следующие методические приемы: · к условию «на первой полке было 5 книг, на второй – 9 книг» составьте вопрос, чтобы задача решалась сложением, вычитанием. · Решите тройку задач «Маме 32 года, дочери 8 лет. Сколько лет маме и дочери вместе? На сколько лет мама старше дочери? Во сколько раз мама старше дочери?» Почему при одних данных получаются разные ответы? · Составление схем прямой и обратной задачи и их сравнение. Автор анализирует процесс решения взаимообратных задач и приводит его схему. Приложения Приложение 1. Результатом … рассуждений относительно задач разных родов является следующее основное положение: для развития у учащихся правильных представлений, а в последствии – и понятий о четырех действиях, соответствующей части начальной арифметики можно построить на задачах и при том на простых. Это соприкасается с вопросом о том, как назвать ту методу, которая разрабатывается в настоящем сочинении. Арифметические задачи вообще должны, при разумном обучении, быть не целью, а только средством обучения арифметике. С их помощью должно вырабатывать и развивать верные и ясные представления и понятия: о четырех действиях, об их смысле и цели и т. п. Поэтому из десяти случаев в девяти задача должна быть исходною точкою обучения арифметике. Вот что говорит известный французский педагог Жан Масе об этом предмете: «Развитие человечества повторятся в каждом малолетнем… Первый, кому пришлось сделать вычисление, начал не с отвлеченных правил, излагаемых в учебниках. Он, очевидно, прежде всего должен был не потеряться при решении практических вопросов и задач, над которыми он мог одержать победу, только пустив в дело все средства своего ума, и он занимался этим искусством вовсе не ради самого искусства. Заставлять ребенка начинать с отвеченного правила и затем предлагать ему задачи – это значит идти наперекор ходу развития человеческого ума… Истинная метода состоит в том, чтобы ставить ребенка в условия, при которых ум человеческий начал изобретать арифметику, и сделать его, так сказать, свидетелем этого изобретения». Такова метода целесообразных задач. Ее точки зрения учитель должен прежде всего себе усвоить, прибегая к задачам чаще для выработки арифметических представлений и понятий, чем для их применения к тем случаям, когда именно эти представления почти неприменимы, как напр., при решении замысловатых задач алгебраического характера. (В духе этой методы составлены и настоящее руководство по предмету методики арифметики, и приноровленные к нему «Новый арифметический задачник для учителей» и «Новый арифметический задачник для учеников», последний в четырех частях). Метода эта названа методою «задач» потом, что задачи, в обширном смысле этого слова, являются исходною точкою во всякий момент обучения. Метода эта названа методою целесообразных задач потому, что для каждой ступени, для каждого учения, для преодоления каждой трудности, надо предлагать ученикам не какие ни попало задачи данного отдела и не задачи ради самого разрешения их, а задачи, сообразованные с исключительною целью предстоящего урока арифметики. Во взгляде же Жана Масе надо, в настоящее время, внести весьма существенную поправку. Учащийся арифметике (и вообще математике) должны быть не только свидетелями изобретения, но активными (по возможности) участниками изобретения арифметики (или математики). Приложение 2 Полезно рисование детьми веточек с листьями, числовых фигур в открытой справа рамке. Сначала учащиеся рисуют
и снизу записывает: 7; затем он присоединяет справа еще один кружок и справа «стенку» и получает и, наконец, приписывает к записанной семерке знак + и одну единицу, т.-е. Получает запись 7 + 1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 1126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.76 (0.018 с.) |


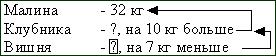 Какие главные слова будут в краткой записи? Малина, клубника, вишня.
Какие главные слова будут в краткой записи? Малина, клубника, вишня. Что известно о привезенной малине? Малины привезли в магазин 32 кг.
Что известно о привезенной малине? Малины привезли в магазин 32 кг.