
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт коэффициента запаса прочностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В данном разделе необходимо определить фактический коэффициент запаса прочности штока гидроцилиндра, а также проверить условие прочности. Вероятный вид разрушения – усталостная поломка. Критерий расчёта – усталостная прочность. Коэффициент запаса прочности может быть определён по формуле
S=
\где S – фактический коэффициент запаса; σпр – предельное напряжение, Максимальное фактическое напряжение σmax определим по формуле
σmax=
где F1 – усилие штока при растяжении (рис 1.1), Н; Amin – минимальная площадь, мм2. Минимальную площадь опасного сечения штока найдём по формуле
Amin=
где d – диаметр опасного сечения, мм. Подставив числа в формулу (1.3), найдём минимальную площадь опасного сечения штока
Amin= Подставляя численное значение Amin в выражение (1.2), получаем
Найдём σmin по формуле
σmin=
где F2 – усилие штока при сжатии, Н. Подставляем численные значения в выражение (1.4)
Построим график изменения напряжения в штоке (рис. 1.2) Цикл изменения напряжения
Рис. 1.2 Из рассмотрения рис. 1.2 следует, что в качестве предельных напряжений σпрследует выбрать предел усталости при произвольном цикле для детали при ограниченном числе циклов разрушения является усталостная поломка.
где Определим коэффициент ассиметрии цикла R = R = Определим предел усталости при симметричном цикле и ограниченном числе циклов
где К0 – коэффициент, учитывающий количество циклов;
Определим значение коэффициента снижения предела выносливости К, который учитывает влияние различных факторов, по формуле [1, с.21] К = где Так как в данном случае деталью является шток, следовательно, заготовка представляет собой прокат вдоль волокон, то есть Определим
где q – коэффициент чувствительности металла к концентрации напряжений; Найдём При Подставляя полученные значения в выражение (1.11), получаем
Коэффициент Подставим численные значения в формулу (1.10) и вычислим К К = Подставляем численные значения в формулу (1.8) и вычисляем
Определим К0 по формуле [1, с.30] К0= где
Считая, что С=5+ m= Подставляем значения в выражение (1.12) К0= Подставляем значения в выражение (1.7), получаем
Определим коэффициент чувствительности детали к асимметрии цикла по формуле [1, с.31]
где
Подставляем численные значения в выражение (1.14)
Теперь может быть вычислен предел усталости в произвольном цикле для детали при ограниченном числе циклов Подставляем численные значения в выражение (1.5)
Так как Проверим условие прочности для данного штока S Вычисляем фактический коэффициент запаса прочности S по формуле (1.1), принимая S= В данном случае, принимая во внимание то, что исходные данные и результаты расчёта имеют пониженную точность, назначаем нормативный коэффициент запаса прочности [S] равным 2,00 [1, с.87]. Таким образом видно, что S=2,1
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 515; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.227.199 (0.008 с.) |

 , (1.1)
, (1.1) ; σmax – максимальное фактическое напряжение,
; σmax – максимальное фактическое напряжение,  , (1.2)
, (1.2)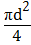 , (1.3)
, (1.3) = 490 мм2
= 490 мм2 =
=  = 91,8
= 91,8 
 , (1.4)
, (1.4) =
=  = -81,6
= -81,6 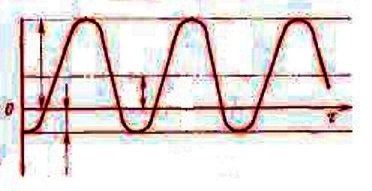
 , так как опыт эксплуатации подобных механизмов показывает, что причиной их
, так как опыт эксплуатации подобных механизмов показывает, что причиной их =
=  <
<  , (1.5)
, (1.5) ;
;  – предел усталости при симметричном цикле и ограниченном числе циклов для детали,
– предел усталости при симметричном цикле и ограниченном числе циклов для детали,  – коэффициент чувствительности детали к асимметрии цикла.
– коэффициент чувствительности детали к асимметрии цикла. (1.6)
(1.6) = -0,890
= -0,890 =
=  К0 (1.7)
К0 (1.7) – предел длительной выносливости для детали при симметричном цикле,
– предел длительной выносливости для детали при симметричном цикле,  =
=  (1.8) Учитывая материал штока – Сталь 40Х и зная, что
(1.8) Учитывая материал штока – Сталь 40Х и зная, что  = 670
= 670  =500
=500  по формуле [1, с.77]
по формуле [1, с.77] = 0,4
= 0,4  = 270
= 270  , (1.10)
, (1.10) – коэффициент концентрации напряжений;
– коэффициент концентрации напряжений;  – коэффициент, учитывающий масштабный фактор;
– коэффициент, учитывающий масштабный фактор; 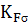 – коэффициент, учитывающий шероховатость поверхности штока;
– коэффициент, учитывающий шероховатость поверхности штока; 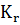 – коэффициент, учитывающий упрочняющие технологии;
– коэффициент, учитывающий упрочняющие технологии;  – коэффициент, учитывающий анизотропию материалов.
– коэффициент, учитывающий анизотропию материалов. = 1+q(
= 1+q( , (1.11)
, (1.11)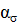 – теоретический коэффициент концентрации напряжений.
– теоретический коэффициент концентрации напряжений.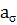 по графику [1, с.78]. Учитывая, что
по графику [1, с.78]. Учитывая, что  =
=  = 1,28 и
= 1,28 и  =
=  = 0,1, получаем
= 0,1, получаем 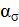 = 1,68.
= 1,68. =
=  = 0,74 коэффициент чувствительности металла к концентрации напряжений q=0,9 [1, с.84]
= 0,74 коэффициент чувствительности металла к концентрации напряжений q=0,9 [1, с.84] = 1+0,9
= 1+0,9  (1,68 - 1) = 1,61
(1,68 - 1) = 1,61 при d =25 мм будет равен
при d =25 мм будет равен  и R = 20 мкм будет равен
и R = 20 мкм будет равен  = 0,71 [1, с.85].
= 0,71 [1, с.85]. = 2,15
= 2,15 =
=  = 125
= 125 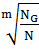 , (1.12)
, (1.12) – базовое число циклов напряжений, соответствующее точке перелома кривой усталости; N – число циклов; m – показатель степени кривой усталости.
– базовое число циклов напряжений, соответствующее точке перелома кривой усталости; N – число циклов; m – показатель степени кривой усталости. = 2
= 2  , определяем m по формуле [1, с.30]
, определяем m по формуле [1, с.30] =
= 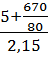 = 6,0 (1.13)
= 6,0 (1.13) = 1,46
= 1,46 = 125
= 125  =
=  , (1.14)
, (1.14) – коэффициент чувствительности к асимметрии цикла, который может быть найден по эмпирической формуле [1, с.31]
– коэффициент чувствительности к асимметрии цикла, который может быть найден по эмпирической формуле [1, с.31] = 0,02+2
= 0,02+2  = 0,02+2
= 0,02+2  =
=  = 0,071
= 0,071 =
= 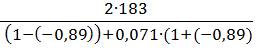 = 192
= 192  =500
=500  , то
, то  =
=  [S] (1.16)
[S] (1.16)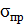 =
= 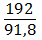 = 2,1
= 2,1 [S]=2,00. То есть при изготовлении штока из стали 40Х по указанным в техническом задании размерам, будет обеспечено отсутствие усталостной поломки при заданных нагрузках и ресурсе в 2
[S]=2,00. То есть при изготовлении штока из стали 40Х по указанным в техническом задании размерам, будет обеспечено отсутствие усталостной поломки при заданных нагрузках и ресурсе в 2 


