
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет стержней на устойчивость. КоэффициентСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уменьшения основного допускаемого напряжения
Для сжатых стержней, кроме условия прочности
должно быть удовлетворено одновременно условие устойчивости:
где Обычно Зависимости (3) и (4) удобны для проверки прочности и устойчивости уже спроектированных стержней. Для удобства проектировочных расчетов введено понятие коэффициент уменьшения основного допускаемого напряжения, который обозначается буквой Найдем отношение Обозначим Получим
Такие таблицы приводятся в учебниках и задачниках по сопротивлению материалов. Пользуясь этими таблицами, удобно подбирать сечения сжатых стержней. С учетом (8.14)условие устойчивости (4) получит вид:
Отсюда следует формула, удобная для подбора размеров сечений:
Практические методы расчета стержней на Устойчивость
I. Проверка сжатой колонны на устойчивость Пример 8.1. Дано: колонна изготовлена из двух стандартных двутавров №30, высотой
Прежде всего решаем вопрос, относительно какой оси
Вычисление Итак: а) таблиц В этом случае определяем по
Для Ст.3, из которых изготовлены двутавры, как было указано выше
Выберем
Условие устойчивости выполняется, следовательно, колонна выдержит в) имеются таблицы
Для Условие устойчивости по (8.15).
Условие устойчивости выполняется. II. Проектирование колонны из стандартных профилей Проектирование рациональной колонны включает три обязательных пункта:
ти. Для сечения колонны, показанного на рис. 8.5 в, этот вопрос решается так: размер « Примечание: В предыдущем примере 8.1. (Проверка на устойчивость) было получено
1. Подбор номера профилей. Используем формулу (8.16) 1 попытка: в (8.16) 2 попытка: в (8.16) подставим Колонна будет оптимальной, если условие устойчивости (8.15) понимать как приблизительное равенство (допускаемая перегрузка до 5% от 2. Определив номер стандартных швеллеров, найдем расстояние «
С другой стороны
Здесь
Приравниваем (6) и (7): 3. Расстояние «
Планки к швеллерам крепятся сваркой или болтами (заклепками). На практике обычно принимают Необходимое число планок « Действительное расстояние
Планки ставятся с двух сторон колонны, как показано на рис. 8.5в, т.е. надо
|
||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 678; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.52.243 (0.011 с.) |

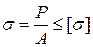 , где
, где 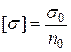 , (3)
, (3)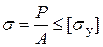 , (4)
, (4)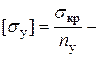 допустимые напряжения на устойчивость,
допустимые напряжения на устойчивость, 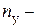 коэффициент запаса устойчивости.
коэффициент запаса устойчивости. имеет более высокое значение, чем коэффициент
имеет более высокое значение, чем коэффициент 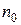 запаса прочности.
запаса прочности.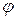 .
.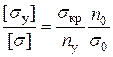 или
или 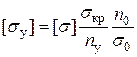 .
.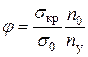 . (5)
. (5)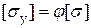 , (8.14)
, (8.14)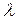 по вышеприведенным формулам или графикам (рис. 8.4) можно найти величины
по вышеприведенным формулам или графикам (рис. 8.4) можно найти величины 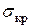 . Далее, зная
. Далее, зная 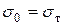 или
или 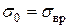 и выбрав коэффициенты
и выбрав коэффициенты 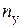 , по зависимости (5) можно составить для данного материала таблицы значений коэффициента
, по зависимости (5) можно составить для данного материала таблицы значений коэффициента 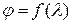 .
. .
.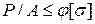 . (8.15)
. (8.15)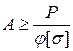 . (8.16)
. (8.16)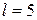 м, нижний конец забетонирован в пол, верхний свободен (
м, нижний конец забетонирован в пол, верхний свободен (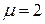 ) и нагружен силой
) и нагружен силой 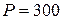 кН.
кН.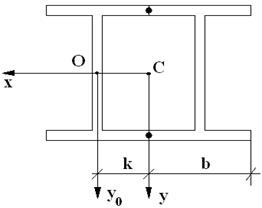
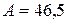 см2,
см2, 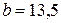 см,
см, 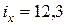 см,
см, 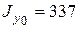 см4.
см4.
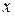 или
или 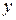 сечения колонны возможна потеря устойчивости. Как указано выше, для этого надо вычислить
сечения колонны возможна потеря устойчивости. Как указано выше, для этого надо вычислить 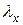 и
и 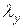 :
: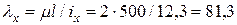 .
.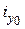 (относительно оси
(относительно оси 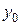 ), а продольный изгиб колонны возможен относительно оси
), а продольный изгиб колонны возможен относительно оси 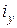 :
:  , где
, где 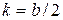 ,
, 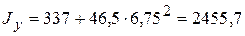 см4,
см4, 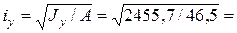
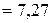 см,
см, 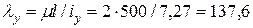 .
.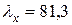 ;
; 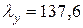 . Следовательно,
. Следовательно, 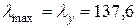 и продольный изгиб колонны возможен относительно оси
и продольный изгиб колонны возможен относительно оси  ). Далее возможны два пути:
). Далее возможны два пути: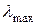 формулу для вычисления
формулу для вычисления 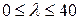
 или
или 
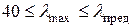
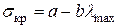 формула Ясинского
формула Ясинского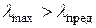
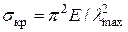 формула Эйлера
формула Эйлера ,
, 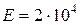 кН/см2. У нас
кН/см2. У нас 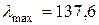 , поэтому выбираем формулу Эйлера:
, поэтому выбираем формулу Эйлера: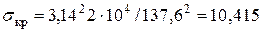 кН/см2.
кН/см2.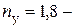 коэффициент запаса устойчивости. Допускаемое
коэффициент запаса устойчивости. Допускаемое 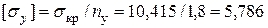 кН/см2 Проверим устойчивость колонны:
кН/см2 Проверим устойчивость колонны: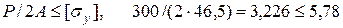 .
.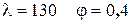
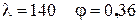

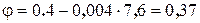
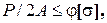 где
где 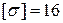 кН/см2 для Ст.3
кН/см2 для Ст.3
 Рис.8.5
Рис.8.5
 и условий закрепления колонны
и условий закрепления колонны 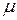 . Расчет выполняют используя таблицы
. Расчет выполняют используя таблицы 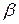 (рис. 8.5в)).
3. Отдельные стандартные профили надо объединить в колонну с помощью поперечных планок или решетки, исключив при этом возможность местной потери устойчивости каждого профиля относительно осей
(рис. 8.5в)).
3. Отдельные стандартные профили надо объединить в колонну с помощью поперечных планок или решетки, исключив при этом возможность местной потери устойчивости каждого профиля относительно осей 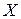 или
или 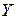 возможна потеря устойчивос-
возможна потеря устойчивос-
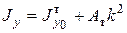 (
(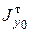 и
и 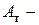 табличные значения из ГОСТа профилей); т.к.
табличные значения из ГОСТа профилей); т.к. 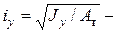 тоже увеличивается,
тоже увеличивается, 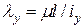 при этом уменьшается, а
при этом уменьшается, а 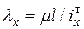 не зависит от размера
не зависит от размера  , а это значит, что возможный продольный изгиб будет относительно оси
, а это значит, что возможный продольный изгиб будет относительно оси  ). Обычно принимают условие равноустойчивости колонны, т.е.
). Обычно принимают условие равноустойчивости колонны, т.е. 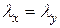 , из которого и определяется расстояние «
, из которого и определяется расстояние «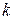 »), можно получить равноустойчивую колонну, которая выдержит значительно большую нагрузку
»), можно получить равноустойчивую колонну, которая выдержит значительно большую нагрузку 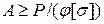 . Здесь площадь
. Здесь площадь  зависит от
зависит от 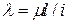 , где
, где  . В итоге получим, что искомая площадь
. В итоге получим, что искомая площадь 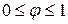 , поэтому вначале примем
, поэтому вначале примем 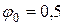 и найдем суммарную площадь сечения колонны
и найдем суммарную площадь сечения колонны  . Далее
. Далее 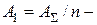 площадь одного профиля (
площадь одного профиля (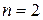 ). По величине
). По величине 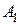 из табл. ГОСТа находим ближайший номер профиля и для него
из табл. ГОСТа находим ближайший номер профиля и для него 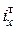 . Вычисляем гибкость
. Вычисляем гибкость 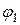 .
.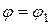 и снова повторим расчет (как в 1 попытке) до определения
и снова повторим расчет (как в 1 попытке) до определения 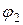 . Здесь уже делаем проверку на устойчивость по (8.15)
. Здесь уже делаем проверку на устойчивость по (8.15) 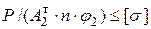 . Здесь
. Здесь 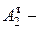 табличное значение площади найденного профиля.
табличное значение площади найденного профиля.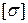 ). Если условие (8.15) не выполняется, или левая часть значительно меньше
). Если условие (8.15) не выполняется, или левая часть значительно меньше 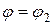 до определения
до определения 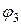 (можно просто изменять в необходимую сторону номера профилей) и снова проверяем устойчивость
(можно просто изменять в необходимую сторону номера профилей) и снова проверяем устойчивость 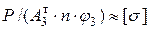 и т.д. Обычно требуется 3¸4 попытки.
и т.д. Обычно требуется 3¸4 попытки.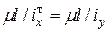 , откуда
, откуда 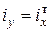 . Тогда
. Тогда . (6).
. (6).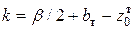 . (8)
. (8)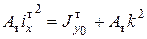 , откуда найдем размер «
, откуда найдем размер «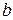 » межу планками находится из условия, чтобы гибкость
» межу планками находится из условия, чтобы гибкость 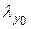 каждого стандартного швеллера колонны между планками относительно оси
каждого стандартного швеллера колонны между планками относительно оси 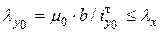 . (9)
. (9)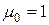 как для стержней с двумя шарнирными концами. Тогда из (9) найдем
как для стержней с двумя шарнирными концами. Тогда из (9) найдем  .
.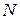 » в колонне
» в колонне 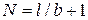 округляется до целого числа.
округляется до целого числа.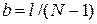
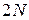 планок.
планок.


