
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Влияние способов закрепления концов стержняСодержание книги
Поиск на нашем сайте
На рис. 8.3 показаны формы потери устойчивости стержней длиной Для других случаев закрепления можно повторить все выкладки, изменяя в каждом случае только граничные условия, и получить соответствующие значения
Рис.8.3
Сравнивая рис. 8.3 а) и 8.3 б), видим, что изогнутая ось стержня, защемленного одним концом, находится в тех же условиях, что и верхняя часть стержня длиной
На рис. 8.3 г) показана потеря устойчивости стержня с двумя защемленными концами. Видно, что она симметрична относительно середины стержня; точки перегиба изогнутой оси (в которых, как известно, изгибающие моменты равны нулю) расположены на четвертях длины стержня. Следовательно, здесь средняя часть стержня длиной Полученные формулы Эйлера при различных закреплениях концов стержня можно записать в общем виде:
Здесь
Для основных случаев закрепления стержней, показанных на рис. 8.3, коэффициент а) один конец защемлен, другой свободный б) с шарнирными концами в) один конец защемлен, другой шарнирный г) с двумя заделанными концами Зная критическую силу, можно найти критическое напряжение, поделив силу на площадь. Так как на деформации стержня местные ослабления площади сечения (отверстиями) сказываются мало, то при расчетах на устойчивость принято использовать полную площадь сечения. Следовательно, в формуле Эйлера
Окончательно Здесь Гибкость стержня – важная характеристика стержней при расчетах их на устойчивость. В (8.9) надо подставлять В неочевидных случаях надо вычислить отдельно: Формула (8.8) – тоже формула Эйлера для критических напряжений.
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.201.71 (0.006 с.) |

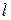 с различными случаями закрепления концов. Случай б) нами рассмотрен при выводе формулы Эйлера. Этот случай называют основным случаем закрепления.
с различными случаями закрепления концов. Случай б) нами рассмотрен при выводе формулы Эйлера. Этот случай называют основным случаем закрепления. . Однако можно пойти другим путем.
. Однако можно пойти другим путем.
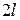 с шарнирными концами. Следовательно,
с шарнирными концами. Следовательно, 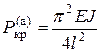 – Эйлерова сила для стержня с одним защемленным концом.
– Эйлерова сила для стержня с одним защемленным концом.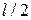 находится в тех же условиях, что и шарнирно закрепленный по концам стержень. Поэтому, подставляя здесь
находится в тех же условиях, что и шарнирно закрепленный по концам стержень. Поэтому, подставляя здесь 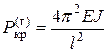 –Эйлерова сила для стержня с двумя защемленными концами.
–Эйлерова сила для стержня с двумя защемленными концами.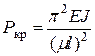 . (8.7)
. (8.7)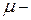 коэффициент приведения длины;
коэффициент приведения длины; приведенная длина стержня.
приведенная длина стержня.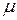 имеет следующие значения:
имеет следующие значения: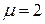 ;
; ;
; ;
;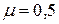 .
. . Тогда
. Тогда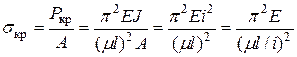 .
. . (8.8)
. (8.8)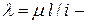 гибкость стержня. (8.9)
гибкость стержня. (8.9)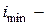 минимальный радиус инерции сечения, поэтому
минимальный радиус инерции сечения, поэтому 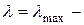 максимальная гибкость. Стержень теряет устойчивость в той плоскости, в которой его гибкость максимальная.
максимальная гибкость. Стержень теряет устойчивость в той плоскости, в которой его гибкость максимальная.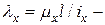 гибкость относительно (вокруг) оси
гибкость относительно (вокруг) оси 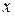 и
и  гибкость относительно оси
гибкость относительно оси 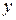 , т.е. в плоскости
, т.е. в плоскости  . Если
. Если 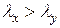 , то
, то 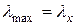 и расчет на продольный изгиб надо вести в плоскости изгиба
и расчет на продольный изгиб надо вести в плоскости изгиба  , а если
, а если 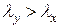 , то
, то 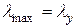 и расчет вести в плоскости
и расчет вести в плоскости 


