
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость сжатых стержней в упругой стадии.Содержание книги
Поиск на нашем сайте
Формула Эйлера
Задачу определения критической силы (напряжений) впервые решил академик Л. Эйлер в 1744 году. Заметим, что сама постановка задачи здесь иная, чем во всех ранее рассматриваемых: если раньше мы определяли деформацию стержня при заданных внешних нагрузках, то здесь ставится обратная задача: задавшись искривлением оси сжатого стержня, следует определить, при каком значении осевой сжимающей силы
Рис.8.1 Для вывода формулы Эйлера рассмотрим шарнирно-опертый, центрально-сжатый стержень постоянного сечения, слегка изогнутый в плоскости наименьшей жесткости. Стержень удерживается в искривленном состоянии силой
Здесь
Подставляя (2) в (1) и деля обе части на
Общий интеграл полученного однородного дифференциального уравнения второго порядка имеет вид:
Это решение включает три неизвестных: А и В – const интегрирования и значение
Рис.8.2 1. При
Таким образом, изогнутая ось является синусоидой
2. При
Отсюда видно, что или А, или Если
Из формулы (8.4) следует, что потеря устойчивости стержня возможна при целом ряде значений силы
Для стержня с шарнирными концами значению критической силы по формуле Эйлера соответствует изгиб по синусоиде с одной полуволной [формула (8.3)] и рис.8.2 при
Значениям критической силы высших порядков (при Константа А осталась неопределенной. Физический смысл ее выясняется, если в уравнение синусоиды (8.6) положить
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.008 с.) |

 такое искривление возможно.
такое искривление возможно.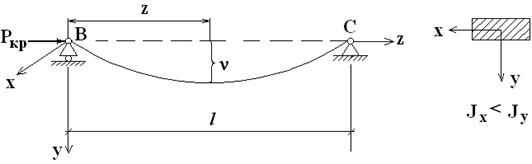
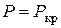 (см. рис. 8.1). Полагая, что материал стержня работает в пределах закона Гука и деформации стержня малы, для решения поставленной задачи можно воспользоваться приближенным дифференциальным уравнением изогнутой оси стержня, полученным ранее:
(см. рис. 8.1). Полагая, что материал стержня работает в пределах закона Гука и деформации стержня малы, для решения поставленной задачи можно воспользоваться приближенным дифференциальным уравнением изогнутой оси стержня, полученным ранее: . (1)
. (1)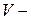 прогибы балки,
прогибы балки, 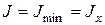 . Изгибающий момент в произвольном сечении
. Изгибающий момент в произвольном сечении 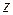 будет равен
будет равен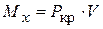 . (2)
. (2) , получим
, получим , где
, где  . (8.1)
. (8.1)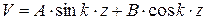 . (8.2)
. (8.2) , т.к. величина критической силы еще неизвестна. Для определения неизвестных используем следующие граничные условия (см. рис.8.1):
, т.к. величина критической силы еще неизвестна. Для определения неизвестных используем следующие граничные условия (см. рис.8.1):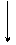





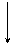





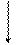


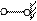


 опора В, поэтому
опора В, поэтому  и, следовательно, из уравнения (8.2) следует
и, следовательно, из уравнения (8.2) следует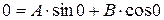 , откуда
, откуда 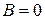 .
.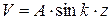 . (8.3)
. (8.3)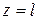 , опора С, поэтому
, опора С, поэтому  .
. равны нулю.
равны нулю.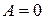 , то из уравнения (8.3) следует, что прогиб в любом сечении стержня равен нулю, т.е. он не потерял устойчивость, а это не соответствует условию задачи. Следовательно необходимо принять, что
, то из уравнения (8.3) следует, что прогиб в любом сечении стержня равен нулю, т.е. он не потерял устойчивость, а это не соответствует условию задачи. Следовательно необходимо принять, что 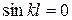 . Последнее условие выполняется, когда
. Последнее условие выполняется, когда 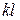 принимает значения:
принимает значения: 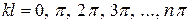 , где
, где 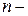 любое целое число. Отсюда
любое целое число. Отсюда 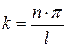 , а т.к.
, а т.к.  и отсюда
и отсюда . (8.4)
. (8.4)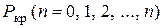 . Для практики интересно знать наименьшее значение осевой сжимающей силы, при которой происходит продольный изгиб. При
. Для практики интересно знать наименьшее значение осевой сжимающей силы, при которой происходит продольный изгиб. При 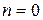 получим
получим 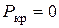 , что не соответствует условиям задачи. Следовательно, наименьшее значение
, что не соответствует условиям задачи. Следовательно, наименьшее значение  принимает при
принимает при 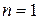 :
: формула Эйлера. (8.5)
формула Эйлера. (8.5)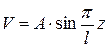 . (8.6)
. (8.6)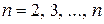 ) соответствуют искривления стержня по синусоидам с двумя, тремя и т.д. полуволнами. Исследования показали, что формы равновесия при
) соответствуют искривления стержня по синусоидам с двумя, тремя и т.д. полуволнами. Исследования показали, что формы равновесия при  и т.д. неустойчивы. Они переходят в устойчивые формы лишь при наличии промежуточных опор в т. В и С (рис. 8.2).
и т.д. неустойчивы. Они переходят в устойчивые формы лишь при наличии промежуточных опор в т. В и С (рис. 8.2).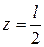 . Тогда
. Тогда 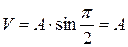 . Следовательно,
. Следовательно, 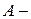 это прогиб стержня в середине. Так как при
это прогиб стержня в середине. Так как при 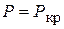 нами принято, что равновесие изогнутого стержня возможно при различных отклонениях его от прямолинейной формы, лишь бы эти отклонения были малыми, то естественно, что прогиб А остался неопределенным.
нами принято, что равновесие изогнутого стержня возможно при различных отклонениях его от прямолинейной формы, лишь бы эти отклонения были малыми, то естественно, что прогиб А остался неопределенным.


