
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет на прочность вращающегося диска методом конечных разностей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Исходными уравнениями являются уравнения равновесия и совместности деформации:
где σr и σθ - радиальные и окружные напряжения в диске; μ - коэффициент Пуассона; Е - модуль упругости материала; α - коэффициент линейного расширения материала. Расчет диска методом конечных разностей основан на приближенном решении системы дифференциальных уравнений (5.1) путем замены дифференциалов конечными разностями. Для расчета диск разбивают рядом концентричных сечений и нумеруют их от 0 до к (рис. 3.1). Замена дифференциалов на конечные разности производится по формулам:
Индекс п указывает номер кольцевого сечения диска.
Рис. 3.1. К расчету диска методом конечных разностей
Для установления связи между напряжениями в п-м и (п - 1)-м сечениях подставим уравнения (5.2) в уравнения (5.1). При этом для величин σr, σθ, r, b, Е и (αt), входящих в уравнение (5.1) без индексов, принимаются их значения на внутреннем (n - 1) сечении кольцевого участка, то есть им приписывают индекс (п - 1). После выполнения необходимых преобразований получаем:
Для сокращения записей введем обозначения:
Подставим обозначения (5.4) в (5.3), получим:
Выразим напряжения Величина окружного напряжения в нулевом сечении Для сплошного диска нулевое сечение проводится вблизи центра диска, где принимают Найдем значения радиальных и окружных напряжений в сечениях диска без центрального отверстия, для чего используем уравнения (5.5). Для первого сечения
где для сокращения записей принимаем A1=V1+ξ1; В1= – С1V1; N1=φ1+λ1; Q1= – μC1V1-ψ1. Для второго сечения
Подставим сюда значения напряжений
где A2=A1ξ2+N1V2; В2=В1ξ2+(Q2-C2)V2; N2=N1φ2+А1λ2; Q2=Q1φ2+B1λ2-μC2V2 -ψ2 Очевидно, что для любого n -го сечения
где
В нулевом сечении формулы (5.6) принимают вид: - для сплошного диска - для диска с центральным отверстием Значения коэффициентов выбираются из условия обращения последних уравнений в тождества, удовлетворяющиеся для любых значений σ0. Для сплошного диска: А0=1, B0=0, N0=1, Q0=0 Для диска с центральным отверстием, свободным от нагрузки: A0=0, В0=0, N0=1, Q0=0. Неизвестное напряжение в нулевом сечении диска σ0 вычисляется по известному радиальному напряжению в к-мсечении диска, которое равно напряжению σrл (рис. 3.1)
откуда
Напряжение σr л от центробежных сил лопаток и замковой части определяется по формуле:
Порядок определения напряжений во вращающемся неравномерно нагретом диске следующий: 1. Для каждого сечения вычисляются вспомогательные величины Vn, ξn, Cn, φn, λn, ψn. 2. Последовательным расчетом, используя формулы (5.7), определяются для каждого сечения коэффициенты Аn, Вn, Nn, Qn. 3. По формуле (5.8) определяются напряжения в нулевом сечении по известной величине напряжения от лопаточного венца σrл и коэффициентами Ак и Вк, 4. Для каждого сечения определяются Точность расчета зависит от числа и расположения выбранных сечений. Обычно назначается не менее десяти сечений. В местах с резким изменением толщины диска сечения выбираются на меньшем расстоянии друг от друга, при этом одно из сечений обязательно должно проходить на радиусе минимальной толщины rb min. Поскольку в диске имеет место плоское напряженное состояние, то за критерий прочности принимается эквивалентное напряжение:
По величине запаса прочности производится прочностная оценка диска:
В качестве предельно допустимого напряжения σпред для дисков турбины принимается предел длительной прочности
Полный расчёт,на прочность вращающегося диска методом конечных разностей, сведём в таблицу 11.
Рисунок 13. График, изменения радиальных и окружных напряжений по длине диска.
Рисунок 14. График, изменения предельных и эквивалентных напряжений по длине диска.
Рисунок 15. График, изменения коэффициента запаса прочности по длине диска.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 655; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.022 с.) |

 ,
, (5.1)
(5.1)











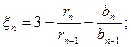





 и
и  для каждого расчетного сечения через напряжение в нулевом сечении. Нулевое сечение для диска с центральным отверстием проводится на радиусе центрального отверстия. Если кромка центрального отверстия не нагружена, то
для каждого расчетного сечения через напряжение в нулевом сечении. Нулевое сечение для диска с центральным отверстием проводится на радиусе центрального отверстия. Если кромка центрального отверстия не нагружена, то  =0; для диска, напрессованного на вал
=0; для диска, напрессованного на вал  = σ0.
= σ0.


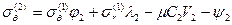
 и
и  выраженные через σ0, получаем
выраженные через σ0, получаем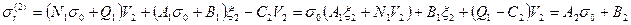




 ;
; = σrл=Акσ0+Вк,
= σrл=Акσ0+Вк,


 ; для дисков компрессоров - предел текучести σ0,2 или предел прочности σв.
; для дисков компрессоров - предел текучести σ0,2 или предел прочности σв.





