
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 2. Поступательное и вращательное движения твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ГЛАВА 2. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА В первой главе мы изучили кинематику точки - то есть движение объекта, который не имеет ни формы, ни размеров, и не был связан с телами конечных размеров. Переходим к кинематике твердого тела, то есть к изучению различных видов движения твердых тел. Изучив движение тела, всегда будем переходить к определению кинематических характеристик движения отдельных точек этого тела. Поступательное движение твердого тела
2.1. Поступательным называется такое движение твердого тела, при котором любая прямая АВ, мысленно проведенная в этом теле, движется, оставаясь параллельной своему начальному направлению (рис.2.1). Классическим примером тела, совершающего поступательное движение, является спарник паровоза. На фото 1 спарники показаны стрелками. Они параллельны рельсам. На рис. 2.2. спарник схематично изображен стержнем CD. Спарник блокирует колеса тепловоза и при вращении колес остается параллельным самому себе, то есть движется поступательно. Точки спарника С и D, равно как и все другие точки спарника, описывают одинаковые по форме траектории в виде циклоиды. Фото 1
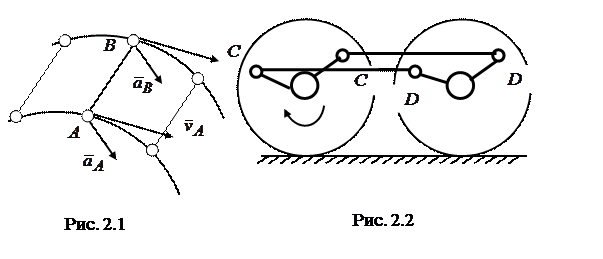
Еще одним примером поступательного движения является движение кабин «колес обозрения». Принципиальная схема движения всех, даже самых знаменитых колес обозрения Мира, одинакова. На фото 2 показано детское колесо обозрения, которое приводится в движение людьми. На фотографии четко видна параллельность всех сидений в разных их положениях. Само колесо вращается, а сидения для детей движутся поступательно. Фото 2
2.2. Основная теорема поступательного движения. При поступательном движении все точки тела описывают тождественные параллельные траектории и имеют в каждый момент времени одинаковые векторы скорости и ускорения Примечание: Две кривые называются тождественными, если они совпадают при наложении. Совпадающие точки тождественных кривых называются соответствующими. Две тождественные кривые называются параллельными, если касательные к ним, проведенные в соответствующих точках, параллельны. Доказательство: Рассмотрим поступательное движение твердого тела в некоторой неподвижной системе отсчета
Продифференцируем по времени равенство (
Последнее равенство с учетом (1.13) можем записать:
Другими словами, векторы скоростей двух произвольных точек тела, совершающего поступательное движение, равны. Следовательно, векторы скоростей всех точек тела равны. Чтобы доказать равенство векторов полных ускорений точек, продифференцируем еще раз равенство
C учетом формулы (1.15) получим:
Следовательно, в силу произвольности выбора точек Тождественность траекторий точек
Рисунок 2.4 иллюстрирует качественную картину расположения векторов скоростей и ускорений трех точек твердого тела (само тело не показано – оно может иметь произвольную форму и размеры), совершающего в некоторый момент времени поступательное движение. Из теоремы, в частности, следует, что одинаковыми по величине и параллельными оказываются и векторы касательных
Вокруг неподвижной оси Вращательное движение (вращение) вообще - одно из самых часто встречающихся движений твердых тел. Оно встречается и в «чистом» виде, когда ось вращения тела неподвижна, и может быть одной из составляющих более сложного движения. Вращаются, например, роторы турбин электростанций, коленчатый вал двигателя, карданный вал и шестерни коробки передач автомобиля, лопасти вентилятора, ротор генератора, вращается пуля в полете. При работе вращаются башенные краны, отдельные части экскаваторов, отдельные части стационарных бетономешалок и «миксеров», развозящих готовый бетон, кузов самосвала при разгрузке, многие части ручного электроинструмента, шпиндели металлообрабатывающих станков и так далее и тому подобное.
2.4. Вращательным движением твердого тела вокруг неподвижной оси будем называть такое его движение, при котором хотя бы две точки тела остаются в покое (рис.2.5). Фото 3
. Фото 4
Часть неподвижной оси вращения (неподвижность оси видна по положению оси относительно неподвижного тела – строящегося здания) отмечена на фотографиях прямой линией На фото 2 показано вращающееся колесо обозрения. Само колесо вращается относительно неподвижной горизонтальной оси, но сидения для детей движутся поступательно.
Равномерное вращение. 2.15. Вращение тела на промежутке времени Из (2.5) следует:
Для определения постоянной интегрирования
Равнопеременное вращение
2.17. Вращательное движение твердого тела на промежутке времени Интегрируя один раз первую из формул (2.7) при e = const и начальных условиях
Вопросы для самоконтроля к главе 2
ГЛАВА 2. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА В первой главе мы изучили кинематику точки - то есть движение объекта, который не имеет ни формы, ни размеров, и не был связан с телами конечных размеров. Переходим к кинематике твердого тела, то есть к изучению различных видов движения твердых тел. Изучив движение тела, всегда будем переходить к определению кинематических характеристик движения отдельных точек этого тела.
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 623; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.92.96 (0.009 с.) |









 ,
,  . А и В – две произвольные точки тела (рис.2.3).
. А и В – две произвольные точки тела (рис.2.3).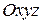 (рис.2.3). На теле выберем две произвольные точки
(рис.2.3). На теле выберем две произвольные точки 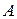 и
и 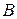 . Эти точки вместе с телом совершают движение. Законы движения этих точек зададим векторным способом:
. Эти точки вместе с телом совершают движение. Законы движения этих точек зададим векторным способом: 
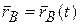 . В точке
. В точке  , оси которой параллельны осям неподвижной системы координат
, оси которой параллельны осям неподвижной системы координат 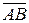 . Вектор
. Вектор  (
(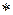 )
)
 (так как
(так как  ), получаем:
), получаем: .
. .
. 
 .
. .
. . Следовательно, в силу произвольности выбора точек
. Следовательно, в силу произвольности выбора точек 
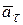 и нормальных
и нормальных 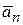 ускорений различных точек тела, так как вектор полного ускорения
ускорений различных точек тела, так как вектор полного ускорения  , а траектории точек тождественны и параллельны.
, а траектории точек тождественны и параллельны.

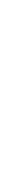







 .
.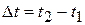 называется равномерным, если угловая скорость тела в этом промежутке времени постоянна (w = const).
называется равномерным, если угловая скорость тела в этом промежутке времени постоянна (w = const). . Проинтегрируем это равенство при w = const. Получим:
. Проинтегрируем это равенство при w = const. Получим: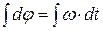 . Отсюда
. Отсюда  . (
. (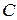 примем начальные условия в виде:
примем начальные условия в виде:  , где
, где 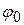 - заданный начальный угол поворота. Тогда уравнение (
- заданный начальный угол поворота. Тогда уравнение (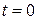 принимает вид:
принимает вид: 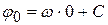 . Находим
. Находим 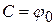 . Видим, что механический смысл постоянной интегрирования
. Видим, что механический смысл постоянной интегрирования 
 (2.8)
(2.8)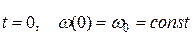 , где
, где  - начальная угловая скорость, получаем:
- начальная угловая скорость, получаем: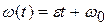 (2.11)
(2.11)


