Задача 2.1. Автомобиль, двигаясь равноускоренно и прямолинейно из состояния покоя по горизонтальному участку пути, за первые десять секунд набрал скорость  . Определить величину ускорений точек кузова.
. Определить величину ускорений точек кузова.
Решение: Прямолинейное движение твердого тела является частным случаем поступательного движения тела.Следовательно, движение кузова автомобиля можно отождествить с движением любой его точки, совершающей прямолинейное движение. В начальный момент времени кузов автомобиля находился в покое ( ). Тогда по формуле (1.72) можно получить величину ускорений точек при прямолинейном движении:
). Тогда по формуле (1.72) можно получить величину ускорений точек при прямолинейном движении:  . Ответ:
. Ответ:  .
.
Задача 2.2. Кривошип  с помощью ползуна 1 приводит в движение кулису 2. Длина кривошипа
с помощью ползуна 1 приводит в движение кулису 2. Длина кривошипа  . Кривошип вращается относительно точки
. Кривошип вращается относительно точки  по закону
по закону  . Определить модуль вектора перемещения и модуль вектора скорости точки А кулисы в момент времени
. Определить модуль вектора перемещения и модуль вектора скорости точки А кулисы в момент времени  .
.

Решение: На рис.2.2 механизм показан в двух положениях – в начальном положении и в положении, для которого надо определить перемещение точки А кулисы. В движение кулису 2 приводит кривошип ОВ. Кривошип ОВ совершает вращательное движение относительно точки О по заданному в условии задачи закону. Кулиса движется поступательно, так как все её контурные линии при движении кулисы остаются параллельными сами себе. Следовательно, по основной теореме поступательного движения (п. 2.2 настоящей главы), все точки кулисы движутся с одинаковыми скоростями и ускорениями, по одинаковым траекториям и имеют одинаковые перемещения. Механизмы создаются так, что движение любой точки одной части механизма сразу «отзывается» движениями точек других частей механизма. По рисунку к задаче видно, что точка В одновременно участвует во вращении кривошипа ОВ и поступательном движении кулисы 2. Перемещение точки В кривошипа (и ползуна) за промежуток времени  изображается вектором
изображается вектором  , а перемещение точки В кулисы изображено вектором
, а перемещение точки В кулисы изображено вектором  . В момент времени
. В момент времени  имеем угол
имеем угол  Тогда модуль перемещения точки В кулисы
Тогда модуль перемещения точки В кулисы  будет равен
будет равен  , так как треугольник
, так как треугольник  - равносторонний. Следовательно,
- равносторонний. Следовательно,  Модуль перемещения точки А кулисы равен модулю перемещения точки В кулисы и равен
Модуль перемещения точки А кулисы равен модулю перемещения точки В кулисы и равен  .
.
Вектор скорости точки В, как точки вращающегося тела (кривошипа ОВ), в любой момент времени перпендикулярен кривошипу ОВ и равен по величине  . В момент времени
. В момент времени  точка В находится в точке
точка В находится в точке  и движется со скоростью
и движется со скоростью  . То есть в данный момент времени кулиса и кривошип находятся в покое. Ответ: Модуль перемещения точки А
. То есть в данный момент времени кулиса и кривошип находятся в покое. Ответ: Модуль перемещения точки А  , скорость точки А равна нулю.
, скорость точки А равна нулю.
Задача 2.3. Тело вращается относительно неподвижной оси по закону  . Исследовать вращение тела при
. Исследовать вращение тела при  и определить угол поворота тела, его угловую скорость и угловое ускорение в момент времени
и определить угол поворота тела, его угловую скорость и угловое ускорение в момент времени 
Решение: Заданное в условии задачи уравнение движения приведем к каноническому виду:  . График этой функции показан на рис.1 к примеру. Механический смысл имеет только та часть кривой, которая лежит в области
. График этой функции показан на рис.1 к примеру. Механический смысл имеет только та часть кривой, которая лежит в области 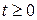 . В начальный момент времени
. В начальный момент времени 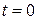 угол поворота тела
угол поворота тела  . Это положение тела принимается за начальное положение. Форма тела при этом не имеет значения, поэтому на рисунках и не показано. В промежутке времени
. Это положение тела принимается за начальное положение. Форма тела при этом не имеет значения, поэтому на рисунках и не показано. В промежутке времени  угол
угол  возрастал по модулю, но был отрицательным. То есть тело вращалось по часовой стрелке, как показано на рис. 2 к примеру. При
возрастал по модулю, но был отрицательным. То есть тело вращалось по часовой стрелке, как показано на рис. 2 к примеру. При  тело вращается против часовой стрелки, при этом, как видно по графику, в момент времени
тело вращается против часовой стрелки, при этом, как видно по графику, в момент времени  угол поворота опять
угол поворота опять  . В этот момент времени тело занимает свое первоначальное положение, то есть то, в котором оно находилось в начальный момент времени
. В этот момент времени тело занимает свое первоначальное положение, то есть то, в котором оно находилось в начальный момент времени 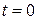 . В отрицательном направлении (по часовой стрелке) тело поворачивается на угол
. В отрицательном направлении (по часовой стрелке) тело поворачивается на угол  (это примерно
(это примерно  ). Полученные результаты позволяют обратить внимание еще раз на то что угол
). Полученные результаты позволяют обратить внимание еще раз на то что угол  , который задается законом вращения – это фактически «угловая координата», отсчитываемая от некоторой произвольно выбранной плоскости. А «угловой путь», пройденный телом от положения
, который задается законом вращения – это фактически «угловая координата», отсчитываемая от некоторой произвольно выбранной плоскости. А «угловой путь», пройденный телом от положения  до того же положения
до того же положения  составлял
составлял  в
в  . Если это не понимать и судить о вращении только по значениям
. Если это не понимать и судить о вращении только по значениям  и
и  , можно было бы заключить, что тело находилось в покое.
, можно было бы заключить, что тело находилось в покое.

Исследуем угловую скорость тела. Угловая скорость  =
=  (
( ). В начальный момент времени при
). В начальный момент времени при 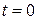 имеем
имеем  =
=  (
( ). Это означает, что тело начинает вращение в исследуемом промежутке времени при начальной угловой скорости
). Это означает, что тело начинает вращение в исследуемом промежутке времени при начальной угловой скорости  - по часовой стрелке. В момент времени
- по часовой стрелке. В момент времени  угловая скорость
угловая скорость  (
( , тогда
, тогда  ). Это момент мгновенного покоя тела, после которого вращение происходит в обратную сторону. Обратите внимание, что при вращении по направлению часовой стрелки (до
). Это момент мгновенного покоя тела, после которого вращение происходит в обратную сторону. Обратите внимание, что при вращении по направлению часовой стрелки (до  ) угловая скорость
) угловая скорость  . Когда тело остановилось (
. Когда тело остановилось ( ) угловая скорость
) угловая скорость  , а при
, а при  угловая скорость
угловая скорость  (тело вращается против часовой стрелки). Угловое ускорение точки
(тело вращается против часовой стрелки). Угловое ускорение точки  - постоянно и положительно. Это означает, что при вращении по часовой стрелке угловая скорость тела уменьшалась (и превратилась в ноль), а при вращении против часовой стрелки, угловая скорость будет увеличиваться. Это подтверждается и видом функции
- постоянно и положительно. Это означает, что при вращении по часовой стрелке угловая скорость тела уменьшалась (и превратилась в ноль), а при вращении против часовой стрелки, угловая скорость будет увеличиваться. Это подтверждается и видом функции  =
=  . Направление вращения тела, угловая скорость и угловое ускорение показано дуговыми стрелками на рис.2 к примеру. При
. Направление вращения тела, угловая скорость и угловое ускорение показано дуговыми стрелками на рис.2 к примеру. При  будем иметь:
будем иметь:  ,
,  =
=  (
( ),
),  . Ответ:
. Ответ:  ,
,  (
( ),
),  .
.
Задача 2.4. Механизм, показанный на рисунке к задаче, состоит из двух параллельных кривошипов одинаковой длины  . С концами кривошипов шарнирно соединен стержень
. С концами кривошипов шарнирно соединен стержень  . Кривошип
. Кривошип  вращается по закону
вращается по закону  (рад), где угол отсчитывается от положительного направления оси
(рад), где угол отсчитывается от положительного направления оси  . В момент времени
. В момент времени  показать положение механизма и определить радиус кривизны траектории тоски
показать положение механизма и определить радиус кривизны траектории тоски 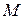 , вектор скорости, векторы касательного, нормального и вектор полного ускорения точки
, вектор скорости, векторы касательного, нормального и вектор полного ускорения точки 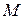 . Найденные векторы изобразить на рисунке.
. Найденные векторы изобразить на рисунке.

Решение: Механизм состоит из трех сочлененных тел – параллельных кривошипов  и
и  и стержня
и стержня  , который в процессе движения остается параллельным оси
, который в процессе движения остается параллельным оси  . Следовательно стержень
. Следовательно стержень  совершает поступательное движение и к нему применима основная теорема поступательного движения. Кривошипы
совершает поступательное движение и к нему применима основная теорема поступательного движения. Кривошипы  и
и  совершают вращение относительно неподвижных осей, проходящих через точки
совершают вращение относительно неподвижных осей, проходящих через точки  и
и 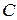 , перпендикулярно к плоскости рисунка по заданному закону. По условию задачи и формулам (2.5) и (2.7) находим:
, перпендикулярно к плоскости рисунка по заданному закону. По условию задачи и формулам (2.5) и (2.7) находим:  (рад),
(рад), 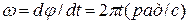 ,
, 
 . В начальный момент времени
. В начальный момент времени  было
было  ,
,  ,
,  . Другими словами, кривошип (и механизм в целом) занимал положение, показанное на рис. 2.4(б), начал движение с нулевой начальной скоростью, равноускоренно. В заданный момент времени
. Другими словами, кривошип (и механизм в целом) занимал положение, показанное на рис. 2.4(б), начал движение с нулевой начальной скоростью, равноускоренно. В заданный момент времени  имеем:
имеем:  (рад),
(рад),  ,
, 
 . Судя по значению
. Судя по значению  (рад), через две секунды после начала движения кривошип, вращаясь равноускоренно, вновь на мгновение занял первоначальное положение (рис. 2.4(б)). При этом он продолжает вращаться против часовой стрелки. Найдем вектор скорости и векторы ускорений точки
(рад), через две секунды после начала движения кривошип, вращаясь равноускоренно, вновь на мгновение занял первоначальное положение (рис. 2.4(б)). При этом он продолжает вращаться против часовой стрелки. Найдем вектор скорости и векторы ускорений точки 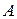 . По формулам (2.16), (2.17), (2.18) имеем:
. По формулам (2.16), (2.17), (2.18) имеем:  ,
,  ,
,  . В момент времени
. В момент времени  :
:  ,
,  ,
,  . Применяя основную теорему поступательного движения (п. 2.2 настоящей главы), окончательно получим:
. Применяя основную теорему поступательного движения (п. 2.2 настоящей главы), окончательно получим:  ,
,  ,
,  . Направление ответствующих векторов показано на рис.2.4(б). Ответ:
. Направление ответствующих векторов показано на рис.2.4(б). Ответ:  ,
,  ,
,  .
.
Задача 2.5. Тело из состояния покоя начинает вращаться и за первые  достигает угловой скорости вращения в
достигает угловой скорости вращения в 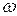 = 36 рад/с. Считая, что тело вращается равноускоренно, определить число полных оборотов, которое сделает тело за указанное время вращения.
= 36 рад/с. Считая, что тело вращается равноускоренно, определить число полных оборотов, которое сделает тело за указанное время вращения.
Решение. Так как первоначально тело находилось в покое, то начальная угловая скорость  . Угол поворота тела будем также отсчитывать от его начального положения, то есть предполагать, что
. Угол поворота тела будем также отсчитывать от его начального положения, то есть предполагать, что  . Для равнопеременного вращения угловое ускорение тела и угол поворота определяются по формулам (2.12) и (2.13):
. Для равнопеременного вращения угловое ускорение тела и угол поворота определяются по формулам (2.12) и (2.13):  и
и  . В нашем случае будем иметь:
. В нашем случае будем иметь:  , а
, а  При одном полном обороте вокруг оси вращения тело поворачивается на угол, равный углу поворота в
При одном полном обороте вокруг оси вращения тело поворачивается на угол, равный углу поворота в  или
или  . Поэтому полный угол поворота всегда равен
. Поэтому полный угол поворота всегда равен  , где
, где 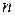 -число оборотов тела вокруг оси вращения. Отсюда для момента времени
-число оборотов тела вокруг оси вращения. Отсюда для момента времени  справедливо уравнение
справедливо уравнение  . Отсюда
. Отсюда  . Ответ:
. Ответ:  .
.
Задача 2.6. Коленчатый вал автомобильного двигателя, имеющий частоту вращения  , был предоставлен самому себе (выключили «зажигание») и из-за трения в подшипниках и в других системах двигателя, остановился в момент времени
, был предоставлен самому себе (выключили «зажигание») и из-за трения в подшипниках и в других системах двигателя, остановился в момент времени  , сделав
, сделав  . Считая вращение вала равнопеременным, определить его угловое ускорение.
. Считая вращение вала равнопеременным, определить его угловое ускорение.
Решение. Угловое ускорение 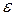 при равнопеременном вращении входит в две основные формулы (2.12), (2.13):
при равнопеременном вращении входит в две основные формулы (2.12), (2.13): 
 . С учетом условия задачи в момент времени
. С учетом условия задачи в момент времени  последние формулы примут вид:
последние формулы примут вид:  ,
,  . Действительно, вал в итоге остановился (
. Действительно, вал в итоге остановился ( ), а угол вращения определяется от того положения вала, при котором он оказался представленным самому себе, то есть
), а угол вращения определяется от того положения вала, при котором он оказался представленным самому себе, то есть  . Исключим время
. Исключим время  из последних формул. Для этого выражаем
из последних формул. Для этого выражаем  из первой формулы (
из первой формулы ( ) и подставляем во вторую. Получаем
) и подставляем во вторую. Получаем  . Окончательно, формула для искомой величины имеет вид:
. Окончательно, формула для искомой величины имеет вид:
 . (*)
. (*)
Определяем угол поворота вала, соответствующий сделанным до остановки одной тысячи оборотов:  . Начальная угловая скорость определяется по формуле (2.10):
. Начальная угловая скорость определяется по формуле (2.10):  Тогда искомая величина углового ускорения
Тогда искомая величина углового ускорения 
 . Ответ:
. Ответ:  .
.
Задача 2.7. Маховик, показанный на рис.(а) к задаче, имеет в данный момент времени  угловую скорость
угловую скорость  и угловое ускорение
и угловое ускорение  . Найти величины скорости
. Найти величины скорости  , касательного
, касательного  , нормального
, нормального  и полного
и полного  ускорений точки
ускорений точки 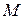 маховика, которая находится на расстоянии
маховика, которая находится на расстоянии  от оси вращения.
от оси вращения.

Решение. Скорость точки 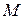 определяется по формуле (2.16). Тогда
определяется по формуле (2.16). Тогда  . Касательное ускорение точки вычисляется по формуле (2.17). Тогда
. Касательное ускорение точки вычисляется по формуле (2.17). Тогда  . Так как знаки угловой скорости
. Так как знаки угловой скорости 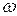 и углового ускорения
и углового ускорения 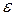 различны (
различны (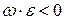 ), то маховик вращается замедленно. Следовательно, вектор касательного ускорение точки
), то маховик вращается замедленно. Следовательно, вектор касательного ускорение точки  направлен по касательной к окружности радиуса
направлен по касательной к окружности радиуса 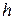 противоположно вектору скорости
противоположно вектору скорости  . Нормальное ускорение точки
. Нормальное ускорение точки 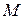 определяется по (2.18). Тогда
определяется по (2.18). Тогда  . Полное ускорение точки вычисляется по формуле (2.19). Тогда
. Полное ускорение точки вычисляется по формуле (2.19). Тогда  = =
= =  . Вектор полного ускорения точки
. Вектор полного ускорения точки  отклонен от вектора
отклонен от вектора  к вектору
к вектору  на угол, тангенс которого вычисляется по формуле (2.20).
на угол, тангенс которого вычисляется по формуле (2.20). 
 =
=  (
( ). Направление векторов
). Направление векторов  показано на рис. (б) к задаче в увеличенном масштабе. Ответ:
показано на рис. (б) к задаче в увеличенном масштабе. Ответ:  ,
,  ,
,  ,
, 
 .
.
Задача 2.8. Механизм состоит из четырех тел – двух вращающихся диска «2» и ступенчатого диска «3», груза «1», подвешенного на нерастяжимой нити, которая намотана на диск «2» без проскальзывания, и рейки «4», плотно прижатой к диску «4». Механизм приводится в движение грузом «1», который движется в положительном направлении оси  по закону
по закону  . Коэффициент
. Коэффициент  имеет единицу измерения
имеет единицу измерения  . Радиусы дисков
. Радиусы дисков  ,
,  ,
,  . В момент времени
. В момент времени  определить угловые скорости
определить угловые скорости  и угловые ускорения
и угловые ускорения  дисков «2» и «3», векторы линейных скоростей
дисков «2» и «3», векторы линейных скоростей 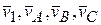 и ускорений
и ускорений  тела «1» и точек
тела «1» и точек  . Сколько оборотов сделает диск «3» за промежуток времени
. Сколько оборотов сделает диск «3» за промежуток времени  .
.


Замечание. Механизм, рассматриваемый в данной задаче, является учебной расчетной моделью механизмов, которые могут входить в состав различных редукторов – механизмов для уменьшения угловых скоростей и увеличения крутящих моментов. Другими словами, механизмов, применяемых для согласования вращательных движений валов двигателей и других частей машин. В качестве примера на фотографиях к задаче показаны два типа редукторов, при этом второй редуктор – «червячный» - преобразует вращение «червяка» относительно одной оси во вращение шестерни относительно другой, перпендикулярной оси. Еще один тип редуктора с коническими шестернями показан на фотографии к задаче 2.20.



Решение: Механизм в момент времени  показан на рисунке (а) к задаче. Линейное перемещение тела «1» и углы поворота тел «2», «3» отсчитываются от соответствующих положений тел в начальный момент времени.
показан на рисунке (а) к задаче. Линейное перемещение тела «1» и углы поворота тел «2», «3» отсчитываются от соответствующих положений тел в начальный момент времени.
1. Рассмотрим движения тела «1», которое совершает прямолинейное поступательное движение.По основной теореме поступательного движения (п. 2.2 настоящей главы) все точки этого тела движутся одинаково – совершают прямолинейные движения. Закон движения тела, то есть закон движения любой его точки, например, точки  задан координатным способом. Судя по закону движения, тело «1» всегда движется в одну сторону, поэтому путь
задан координатным способом. Судя по закону движения, тело «1» всегда движется в одну сторону, поэтому путь  , пройденный точкой
, пройденный точкой  за время
за время  , равен координате точки
, равен координате точки  . Проекции вектора скорости и ускорения точки
. Проекции вектора скорости и ускорения точки  равны:
равны:  ,
,  .В момент времени
.В момент времени  имеем:
имеем:  ,
,  ,
,  .
.
2. Рассмотрим движение тела «2», которое совершает вращательное движение относительно неподвижной оси подшипника, перпендикулярной плоскости рисунка. Так как нить считается нерастяжимой и намотана на диск без проскальзывания, то в точках соприкосновения точки нити и диска имеют равные скорости и ускорения:  ,
,  . С другой стороны, по (2.16) и (2.17) имеем:
. С другой стороны, по (2.16) и (2.17) имеем:  ,
,  Тогда
Тогда  =
=  ,
,  =
=  , где
, где  - угловая скорость и угловое ускорение второго диска соответственно. По (2.18) находим величину нормального ускорения
- угловая скорость и угловое ускорение второго диска соответственно. По (2.18) находим величину нормального ускорения  =
=  .
.
В момент времени  получим:
получим: 
 ,
, 
 ,
,  ,
, 
 ,
, 
 . Величину вектора полного ускорения вычислим по формуле
. Величину вектора полного ускорения вычислим по формуле  =
=  =
=  .
.
3. Рассмотрим движение тела «3». Так как диски находятся в зацеплении без проскальзывания, то в точке  можно записать:
можно записать:  ,
,  , где индексы «2» и «3» указывают на соответствующие диски. Тогда
, где индексы «2» и «3» указывают на соответствующие диски. Тогда  ,
,  . Отсюда
. Отсюда  ,
,  . Для точки
. Для точки 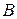 будем иметь:
будем иметь: 
 =
=  ,
, 
 =
=  ,
,  В момент времени
В момент времени  получим:
получим: 
 ,
, 
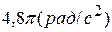 ,
,  ,
,  =
=  ,
, 
 .
.
4. Рассмотрим тело «4», которое совершает поступательное движение. В точке  оно соприкасается с диском «3». Следовательно
оно соприкасается с диском «3». Следовательно 
 ,
,  =
=  .
.
5. Наконец, определим число оборотов третьего диска. Первое тело за заданный промежуток времени прошло расстояние  . Такое же расстояние проходит любая точка нерастяжимой нити. Точки диска «2», соприкасающиеся с намотанной на него нитью проходят тоже такой же путь по окружности диска. При одном полном повороте диска его произвольная точка проходит путь, равный длине окружности диска
. Такое же расстояние проходит любая точка нерастяжимой нити. Точки диска «2», соприкасающиеся с намотанной на него нитью проходят тоже такой же путь по окружности диска. При одном полном повороте диска его произвольная точка проходит путь, равный длине окружности диска  . Число поворотов
. Число поворотов 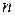 получим, поделив путь, пройденный точкой нити, на длину окружности
получим, поделив путь, пройденный точкой нити, на длину окружности  . Другими словами, второй диск совершил пол оборота. Точки диска «3» пройдут тот же путь
. Другими словами, второй диск совершил пол оборота. Точки диска «3» пройдут тот же путь  . Поделив этот путь на длину меньшей окружности третьего диска, получим:
. Поделив этот путь на длину меньшей окружности третьего диска, получим:  Интересно отметить, что
Интересно отметить, что  .
.
§ 2.8. Задачи для самостоятельного решения на поступательное и вращательное движение твердого тела к главе 2.
Задача 2.9. Шкив радиусом 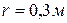 , вращается равномерно с частотой
, вращается равномерно с частотой  . Найти его угловую скорость
. Найти его угловую скорость 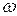 в рад/с, а также скорость и ускорение точки, лежащей на внешнем ободе шкива. Ответ:
в рад/с, а также скорость и ускорение точки, лежащей на внешнем ободе шкива. Ответ:  ,
,  ,
,  .
.
Задача 2.10. Лопасти вентилятора вращаются с частотой  . Какой длины
. Какой длины  можно сделать отдельную лопасть вентилятора, если максимальная скорость точек вентилятора
можно сделать отдельную лопасть вентилятора, если максимальная скорость точек вентилятора  не должна превышать
не должна превышать  ? Ответ:
? Ответ: 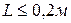 .
.
Задача 2.11. На вращающийся вал плотно насажен шкив диаметром  , который вращается вместе с валом.Скорость точек
, который вращается вместе с валом.Скорость точек  , лежащих на внешнем ободе шкива, равна в данный момент времени
, лежащих на внешнем ободе шкива, равна в данный момент времени  . Определить частоту вращения шкива
. Определить частоту вращения шкива 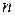 . Ответ:
. Ответ:  .
.
Задача 2.12. Маховик радиуса  вращается равномерно вокруг своей оси, делая
вращается равномерно вокруг своей оси, делая  оборотов за половину секунды. Определить скорость и ускорение точки, лежащей на внешнем ободе маховика. Ответ:
оборотов за половину секунды. Определить скорость и ускорение точки, лежащей на внешнем ободе маховика. Ответ:  ,
,  .
.

Задача 2.13. Механизм состоит из двух зубчатых колес 1 и 2, находящихся в зацеплении, и кривошипного механизма  . Точки
. Точки  лежат на одной горизонтальной прямой. Кривошипы
лежат на одной горизонтальной прямой. Кривошипы  и
и  параллельны и имеют равную длину
параллельны и имеют равную длину  . В точках
. В точках  имеют место шарнирные соединения. Механизм приводится в движение вращением против часовой стрелки кривошипа
имеют место шарнирные соединения. Механизм приводится в движение вращением против часовой стрелки кривошипа  , который имеет общую ось вращения с зубчатым колесом 2 и в точке
, который имеет общую ось вращения с зубчатым колесом 2 и в точке 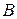 соединен с ним при помощи шарнира. Определить величину скорости
соединен с ним при помощи шарнира. Определить величину скорости 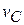 точки
точки 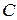 , если величина скорости точки
, если величина скорости точки 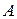 в данный момент времени известна и
в данный момент времени известна и  .
.  . Ответ:
. Ответ:  .
.
Задача 2.14. Зубчатое колесо 1 (см. условие и рис. к зад. 2.13) вращается согласно закону  . Определить величину вектора полного ускорения
. Определить величину вектора полного ускорения  точки
точки 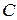 в момент времени
в момент времени  , если
, если  ,
,  . Ответ:
. Ответ:  .
.
Задача 2.15. Величина нормального ускорения точки 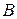 зубчатого колеса 2 равно
зубчатого колеса 2 равно  (см. условие и рис. к зад. 2.13). Определить величину скорости точки
(см. условие и рис. к зад. 2.13). Определить величину скорости точки 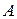 , если
, если  ,
,  . Ответ:
. Ответ:  .
.
Задача 2.16. В период разгона маховик паровой турбины (см. рис. к задаче 2.7) вращается по закону  Диаметр маховика
Диаметр маховика  . В момент времени
. В момент времени  определить количество оборотов
определить количество оборотов  , которое сделает маховик к этому моменту времени, угловую скорость
, которое сделает маховик к этому моменту времени, угловую скорость 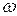 и угловое ускорение
и угловое ускорение 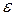 маховика, а также величины линейной скорости
маховика, а также величины линейной скорости  , касательного
, касательного  , нормального
, нормального  и полного
и полного  ускорений точек, лежащих на окружности маховика. Ответ:
ускорений точек, лежащих на окружности маховика. Ответ: 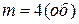 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Задача 2.17. Конькобежец проходит закругление беговой дорожки стадиона. Центр тяжести спортсмена имеет в этот момент времени величину касательного ускорения  и величину полного ускорения
и величину полного ускорения  . Определить в этот момент времени радиус кривизны траектории центра тяжести
. Определить в этот момент времени радиус кривизны траектории центра тяжести 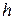 и угловую скорость этого воображаемого радиуса
и угловую скорость этого воображаемого радиуса 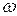 , если угловое ускорение радиуса
, если угловое ускорение радиуса  . Ответ:
. Ответ:  ,
,  .
.
Задача 2.18. Определить угловые скорости  , угловые ускорения
, угловые ускорения  , линейные скорости
, линейные скорости  , касательные
, касательные  , нормальные
, нормальные  и полные
и полные  ускорения концов секундной, минутной и часовой стрелок часов, если их длины соответственно равны
ускорения концов секундной, минутной и часовой стрелок часов, если их длины соответственно равны  ,
,  ,
,  . Ответ:
. Ответ:  ,
,  ,
,  ,
, 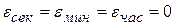 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.





 . Определить величину ускорений точек кузова.
. Определить величину ускорений точек кузова. ). Тогда по формуле (1.72) можно получить величину ускорений точек при прямолинейном движении:
). Тогда по формуле (1.72) можно получить величину ускорений точек при прямолинейном движении:  . Ответ:
. Ответ:  .
. с помощью ползуна 1 приводит в движение кулису 2. Длина кривошипа
с помощью ползуна 1 приводит в движение кулису 2. Длина кривошипа  . Кривошип вращается относительно точки
. Кривошип вращается относительно точки  по закону
по закону  . Определить модуль вектора перемещения и модуль вектора скорости точки А кулисы в момент времени
. Определить модуль вектора перемещения и модуль вектора скорости точки А кулисы в момент времени  .
.

 изображается вектором
изображается вектором  , а перемещение точки В кулисы изображено вектором
, а перемещение точки В кулисы изображено вектором  . В момент времени
. В момент времени  имеем угол
имеем угол  Тогда модуль перемещения точки В кулисы
Тогда модуль перемещения точки В кулисы  будет равен
будет равен  , так как треугольник
, так как треугольник  - равносторонний. Следовательно,
- равносторонний. Следовательно,  Модуль перемещения точки А кулисы равен модулю перемещения точки В кулисы и равен
Модуль перемещения точки А кулисы равен модулю перемещения точки В кулисы и равен  . В момент времени
. В момент времени  и движется со скоростью
и движется со скоростью  . То есть в данный момент времени кулиса и кривошип находятся в покое. Ответ: Модуль перемещения точки А
. То есть в данный момент времени кулиса и кривошип находятся в покое. Ответ: Модуль перемещения точки А  , скорость точки А равна нулю.
, скорость точки А равна нулю. . Исследовать вращение тела при
. Исследовать вращение тела при  и определить угол поворота тела, его угловую скорость и угловое ускорение в момент времени
и определить угол поворота тела, его угловую скорость и угловое ускорение в момент времени 
 . График этой функции показан на рис.1 к примеру. Механический смысл имеет только та часть кривой, которая лежит в области
. График этой функции показан на рис.1 к примеру. Механический смысл имеет только та часть кривой, которая лежит в области 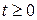 . В начальный момент времени
. В начальный момент времени 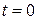 угол поворота тела
угол поворота тела  . Это положение тела принимается за начальное положение. Форма тела при этом не имеет значения, поэтому на рисунках и не показано. В промежутке времени
. Это положение тела принимается за начальное положение. Форма тела при этом не имеет значения, поэтому на рисунках и не показано. В промежутке времени  угол
угол  возрастал по модулю, но был отрицательным. То есть тело вращалось по часовой стрелке, как показано на рис. 2 к примеру. При
возрастал по модулю, но был отрицательным. То есть тело вращалось по часовой стрелке, как показано на рис. 2 к примеру. При  тело вращается против часовой стрелки, при этом, как видно по графику, в момент времени
тело вращается против часовой стрелки, при этом, как видно по графику, в момент времени  угол поворота опять
угол поворота опять  (это примерно
(это примерно  ). Полученные результаты позволяют обратить внимание еще раз на то что угол
). Полученные результаты позволяют обратить внимание еще раз на то что угол  до того же положения
до того же положения  составлял
составлял  в
в  . Если это не понимать и судить о вращении только по значениям
. Если это не понимать и судить о вращении только по значениям 
 =
=  (
( ). В начальный момент времени при
). В начальный момент времени при  =
=  (
( - по часовой стрелке. В момент времени
- по часовой стрелке. В момент времени  угловая скорость
угловая скорость  (
( , тогда
, тогда  ) угловая скорость
) угловая скорость  . Когда тело остановилось (
. Когда тело остановилось ( (тело вращается против часовой стрелки). Угловое ускорение точки
(тело вращается против часовой стрелки). Угловое ускорение точки  - постоянно и положительно. Это означает, что при вращении по часовой стрелке угловая скорость тела уменьшалась (и превратилась в ноль), а при вращении против часовой стрелки, угловая скорость будет увеличиваться. Это подтверждается и видом функции
- постоянно и положительно. Это означает, что при вращении по часовой стрелке угловая скорость тела уменьшалась (и превратилась в ноль), а при вращении против часовой стрелки, угловая скорость будет увеличиваться. Это подтверждается и видом функции  будем иметь:
будем иметь:  ,
,  =
=  (
( . Ответ:
. Ответ:  ,
,  (
( . С концами кривошипов шарнирно соединен стержень
. С концами кривошипов шарнирно соединен стержень  . Кривошип
. Кривошип  вращается по закону
вращается по закону  (рад), где угол отсчитывается от положительного направления оси
(рад), где угол отсчитывается от положительного направления оси  . В момент времени
. В момент времени 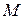 , вектор скорости, векторы касательного, нормального и вектор полного ускорения точки
, вектор скорости, векторы касательного, нормального и вектор полного ускорения точки  и стержня
и стержня 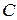 , перпендикулярно к плоскости рисунка по заданному закону. По условию задачи и формулам (2.5) и (2.7) находим:
, перпендикулярно к плоскости рисунка по заданному закону. По условию задачи и формулам (2.5) и (2.7) находим: 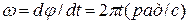 ,
, 
 . В начальный момент времени
. В начальный момент времени  было
было  ,
,  ,
,  . Другими словами, кривошип (и механизм в целом) занимал положение, показанное на рис. 2.4(б), начал движение с нулевой начальной скоростью, равноускоренно. В заданный момент времени
. Другими словами, кривошип (и механизм в целом) занимал положение, показанное на рис. 2.4(б), начал движение с нулевой начальной скоростью, равноускоренно. В заданный момент времени  имеем:
имеем:  (рад),
(рад),  ,
, 
 (рад), через две секунды после начала движения кривошип, вращаясь равноускоренно, вновь на мгновение занял первоначальное положение (рис. 2.4(б)). При этом он продолжает вращаться против часовой стрелки. Найдем вектор скорости и векторы ускорений точки
(рад), через две секунды после начала движения кривошип, вращаясь равноускоренно, вновь на мгновение занял первоначальное положение (рис. 2.4(б)). При этом он продолжает вращаться против часовой стрелки. Найдем вектор скорости и векторы ускорений точки 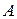 . По формулам (2.16), (2.17), (2.18) имеем:
. По формулам (2.16), (2.17), (2.18) имеем:  ,
,  ,
,  . В момент времени
. В момент времени  ,
,  ,
,  . Применяя основную теорему поступательного движения (п. 2.2 настоящей главы), окончательно получим:
. Применяя основную теорему поступательного движения (п. 2.2 настоящей главы), окончательно получим:  ,
,  ,
,  . Направление ответствующих векторов показано на рис.2.4(б). Ответ:
. Направление ответствующих векторов показано на рис.2.4(б). Ответ:  достигает угловой скорости вращения в
достигает угловой скорости вращения в 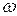 = 36 рад/с. Считая, что тело вращается равноускоренно, определить число полных оборотов, которое сделает тело за указанное время вращения.
= 36 рад/с. Считая, что тело вращается равноускоренно, определить число полных оборотов, которое сделает тело за указанное время вращения. . Для равнопеременного вращения угловое ускорение тела и угол поворота определяются по формулам (2.12) и (2.13):
. Для равнопеременного вращения угловое ускорение тела и угол поворота определяются по формулам (2.12) и (2.13):  и
и  . В нашем случае будем иметь:
. В нашем случае будем иметь:  , а
, а  При одном полном обороте вокруг оси вращения тело поворачивается на угол, равный углу поворота в
При одном полном обороте вокруг оси вращения тело поворачивается на угол, равный углу поворота в  или
или  . Поэтому полный угол поворота всегда равен
. Поэтому полный угол поворота всегда равен  , где
, где 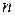 -число оборотов тела вокруг оси вращения. Отсюда для момента времени
-число оборотов тела вокруг оси вращения. Отсюда для момента времени  . Отсюда
. Отсюда  . Ответ:
. Ответ:  .
. , был предоставлен самому себе (выключили «зажигание») и из-за трения в подшипниках и в других системах двигателя, остановился в момент времени
, был предоставлен самому себе (выключили «зажигание») и из-за трения в подшипниках и в других системах двигателя, остановился в момент времени  , сделав
, сделав  . Считая вращение вала равнопеременным, определить его угловое ускорение.
. Считая вращение вала равнопеременным, определить его угловое ускорение.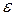 при равнопеременном вращении входит в две основные формулы (2.12), (2.13):
при равнопеременном вращении входит в две основные формулы (2.12), (2.13):  ,
,  . Действительно, вал в итоге остановился (
. Действительно, вал в итоге остановился ( ), а угол вращения определяется от того положения вала, при котором он оказался представленным самому себе, то есть
), а угол вращения определяется от того положения вала, при котором он оказался представленным самому себе, то есть  из последних формул. Для этого выражаем
из последних формул. Для этого выражаем  ) и подставляем во вторую. Получаем
) и подставляем во вторую. Получаем  . Окончательно, формула для искомой величины имеет вид:
. Окончательно, формула для искомой величины имеет вид: . (*)
. (*) . Начальная угловая скорость определяется по формуле (2.10):
. Начальная угловая скорость определяется по формуле (2.10):  Тогда искомая величина углового ускорения
Тогда искомая величина углового ускорения 
 . Ответ:
. Ответ:  .
. угловую скорость
угловую скорость  и угловое ускорение
и угловое ускорение  . Найти величины скорости
. Найти величины скорости  , касательного
, касательного  , нормального
, нормального  и полного
и полного  ускорений точки
ускорений точки  от оси вращения.
от оси вращения.
 . Касательное ускорение точки вычисляется по формуле (2.17). Тогда
. Касательное ускорение точки вычисляется по формуле (2.17). Тогда  . Так как знаки угловой скорости
. Так как знаки угловой скорости 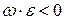 ), то маховик вращается замедленно. Следовательно, вектор касательного ускорение точки
), то маховик вращается замедленно. Следовательно, вектор касательного ускорение точки  направлен по касательной к окружности радиуса
направлен по касательной к окружности радиуса 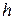 противоположно вектору скорости
противоположно вектору скорости  . Нормальное ускорение точки
. Нормальное ускорение точки  . Полное ускорение точки вычисляется по формуле (2.19). Тогда
. Полное ускорение точки вычисляется по формуле (2.19). Тогда  = =
= =  . Вектор полного ускорения точки
. Вектор полного ускорения точки  отклонен от вектора
отклонен от вектора 
 =
=  (
( ). Направление векторов
). Направление векторов  показано на рис. (б) к задаче в увеличенном масштабе. Ответ:
показано на рис. (б) к задаче в увеличенном масштабе. Ответ:  ,
,  ,
,  ,
, 
 .
. по закону
по закону  . Коэффициент
. Коэффициент  имеет единицу измерения
имеет единицу измерения  . Радиусы дисков
. Радиусы дисков  ,
,  ,
,  . В момент времени
. В момент времени  и угловые ускорения
и угловые ускорения  дисков «2» и «3», векторы линейных скоростей
дисков «2» и «3», векторы линейных скоростей 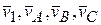 и ускорений
и ускорений  тела «1» и точек
тела «1» и точек  . Сколько оборотов сделает диск «3» за промежуток времени
. Сколько оборотов сделает диск «3» за промежуток времени 


 задан координатным способом. Судя по закону движения, тело «1» всегда движется в одну сторону, поэтому путь
задан координатным способом. Судя по закону движения, тело «1» всегда движется в одну сторону, поэтому путь  , пройденный точкой
, пройденный точкой  . Проекции вектора скорости и ускорения точки
. Проекции вектора скорости и ускорения точки  ,
,  .В момент времени
.В момент времени  ,
,  ,
,  .
. ,
,  . С другой стороны, по (2.16) и (2.17) имеем:
. С другой стороны, по (2.16) и (2.17) имеем:  ,
,  Тогда
Тогда  =
=  ,
,  =
=  , где
, где  - угловая скорость и угловое ускорение второго диска соответственно. По (2.18) находим величину нормального ускорения
- угловая скорость и угловое ускорение второго диска соответственно. По (2.18) находим величину нормального ускорения  =
=  .
.
 ,
, 
 ,
,  ,
, 
 ,
, 
 . Величину вектора полного ускорения вычислим по формуле
. Величину вектора полного ускорения вычислим по формуле  =
=  =
=  .
. можно записать:
можно записать:  ,
,  , где индексы «2» и «3» указывают на соответствующие диски. Тогда
, где индексы «2» и «3» указывают на соответствующие диски. Тогда  ,
,  . Отсюда
. Отсюда  ,
,  . Для точки
. Для точки 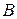 будем иметь:
будем иметь: 
 =
=  ,
, 
 =
=  ,
,  В момент времени
В момент времени 
 ,
, 
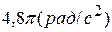 ,
,  ,
,  =
=  ,
, 
 .
. оно соприкасается с диском «3». Следовательно
оно соприкасается с диском «3». Следовательно 
 ,
,  =
=  . Число поворотов
. Число поворотов  . Другими словами, второй диск совершил пол оборота. Точки диска «3» пройдут тот же путь
. Другими словами, второй диск совершил пол оборота. Точки диска «3» пройдут тот же путь  Интересно отметить, что
Интересно отметить, что  .
.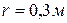 , вращается равномерно с частотой
, вращается равномерно с частотой  . Найти его угловую скорость
. Найти его угловую скорость  ,
,  ,
,  .
. . Какой длины
. Какой длины  не должна превышать
не должна превышать  ? Ответ:
? Ответ: 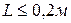 .
. , который вращается вместе с валом.Скорость точек
, который вращается вместе с валом.Скорость точек  . Определить частоту вращения шкива
. Определить частоту вращения шкива  .
. вращается равномерно вокруг своей оси, делая
вращается равномерно вокруг своей оси, делая  оборотов за половину секунды. Определить скорость и ускорение точки, лежащей на внешнем ободе маховика. Ответ:
оборотов за половину секунды. Определить скорость и ускорение точки, лежащей на внешнем ободе маховика. Ответ:  ,
,  .
.
 . Точки
. Точки  лежат на одной горизонтальной прямой. Кривошипы
лежат на одной горизонтальной прямой. Кривошипы  и
и  параллельны и имеют равную длину
параллельны и имеют равную длину  . В точках
. В точках  имеют место шарнирные соединения. Механизм приводится в движение вращением против часовой стрелки кривошипа
имеют место шарнирные соединения. Механизм приводится в движение вращением против часовой стрелки кривошипа 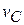 точки
точки  .
.  . Ответ:
. Ответ:  .
. . Определить величину вектора полного ускорения
. Определить величину вектора полного ускорения  точки
точки  .
. (см. условие и рис. к зад. 2.13). Определить величину скорости точки
(см. условие и рис. к зад. 2.13). Определить величину скорости точки  .
. Диаметр маховика
Диаметр маховика  . В момент времени
. В момент времени  , которое сделает маховик к этому моменту времени, угловую скорость
, которое сделает маховик к этому моменту времени, угловую скорость  , нормального
, нормального  и полного
и полного 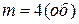 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. и величину полного ускорения
и величину полного ускорения  . Определить в этот момент времени радиус кривизны траектории центра тяжести
. Определить в этот момент времени радиус кривизны траектории центра тяжести  . Ответ:
. Ответ:  ,
,  .
. , угловые ускорения
, угловые ускорения  , линейные скорости
, линейные скорости  , касательные
, касательные  , нормальные
, нормальные  и полные
и полные  ускорения концов секундной, минутной и часовой стрелок часов, если их длины соответственно равны
ускорения концов секундной, минутной и часовой стрелок часов, если их длины соответственно равны  ,
,  ,
,  . Ответ:
. Ответ:  ,
,  ,
,  ,
, 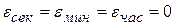 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.


