

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Основные формы дифференциальных уравнений динамики материальной точки
Похожие статьи вашей тематики
Ускорение материальной точки массы m, движущейся под действием приложенных к ней сил F1, F2,..., Fn, определяется с помощью основного закона динамики (второго закона Ньютона) в сочетании с законом независимости действия сил: mа = F1+ F2+...+ Fn.
Дифференциальные уравнения движения материальной точки в проекциях на оси неподвижных декартовых координат имеют вид
mх" =  , mу" = , mу" =  , mz" = , mz" =  . .
Где х", у", z"- проекции ускорения а, а Fkх; Fkу; Fkz — проекции силыF на соответствующие оси декартовых координат.
Дифференциальные уравнения плоского движения материальной точки в полярных координатах имеют вид m(r"—rφ'2) =  , ,  = = 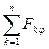
здесь r — радиус-вектор точки, φ — полярный угол.
Дифференциальные уравнения движения материальной точки записываются соответственно выбранной системе координат. Так, дифференциальные уравнения можно составить в цилиндрических, сферических и других криволинейных координатах.
С помощью дифференциальных уравнений движения материальной точки можно решать две основные задачи динамики: прямую и обратную. Прямой называется задача, в которой по заданным движению и массе материальной точки определяется равнодействующая сил, приложенных к этой точке. Обратной называется задача, в которой по заданным силам и массе материальной точки определяется ее движение.
Колебательные движения
Линейными называются колебания, описываемые линейными дифференциальными уравнениями.
При движении материальной точки может действовать сила упругости, стремящаяся вернуть точку к некоторому положению. Эта сила упругости называется восстанавливающей, В большинстве задач рассматривается восстанавливающая сила F изменяющаяся по линейному закону (по закону Гука).
При растяжении пружины эта сила прямо пропорциональна удлинению F=—с Δ х, где Δх — смещение конца пружины из ненапряженного состояния, с — коэффициент упругости (коэффициент жесткости), численно равный силе, которую надо приложить к пружине для того, чтобы изменить ее длину на единицу.
Свободными называются колебания материальной точки, которые происходят под действием восстанавливающей силы. При движении материальной точки М массы m по горизонтальной оси х под действием восстанавливающей силы F, равной по модулю F = с|х|, имеет место дифференциальное уравнение движения. x″+k2x=0, где k2=с/m.
Влияние силы сопротивления на свободные колебания материальной точки. При движении материальной точки в среде, препятствующей движению (воздух, жидкость), возникает сила сопротивления движению. Эта сила при малых скоростях движения точки может приближенно считаться прямо пропорциональной первой степени скорости точки: R = βv, где β — постоянный коэффициент; при больших скоростях — квадрату скорости точки: R = β1v2, где β1— постоянный коэффициент.
Рассмотрим свободные колебания материальной точки при наличии силы, пропорциональной первой степени скорости точки: R = βv. В этом случае дифференциальное уравнение движения материальной точки имеет вид: x″+2n x′+k2x=0, где k2=с/m, 2n= β/ m.
Вынужденные колебания. Резонанс. Рассмотрим случай, когда на колебательную систему действует периодическая внешняя сила f(t)=а sinω1t, предполагая для простоты, что сопротивление среды отсутствует (μ=0). В этом случае уравнение движения принимает вид 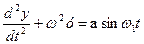
Это линейное неоднородное уравнение с постоянными коэффициентами. Общее решение этого уравнения является суммой общего решения у соответствующего однородного уравнения, и частного решения ỹ неоднородного уравнения, которое надо найти.
Рассмотрим отдельно два случая.
а) ω≠ω1, т. е. частота внешней периодической силы отлична от частоты свободных колебаний груза. Так как число iω не совпадает с корнем характеристического уравнения k2 +ω2= = 0, то частное решение можно найти в виде
ỹ = А соsω1 t + В sin ω1 t.
Дифференцируя ỹ дважды и подставляя и ỹ и ỹ″ в уравнение найдем: В =  , А=0. , А=0.
Таким образом, ỹ =  sinω1t и общее решение уравнения имеет вид: sinω1t и общее решение уравнения имеет вид:
у = ỹ + У =  sinω1t + А sin(ωt+φ) sinω1t + А sin(ωt+φ)
Отсюда следует что частное решение ỹ определяет колебание системы, создаваемое внешней силой, общее решение У=А sin(ωt+φ) — свободное колебание груза, а общее решение у — сложное колебательное движение, получающееся в результате сложения двух колебаний с разными частотами ω и ω1.
В этом случае амплитуда постоянна, и если ω и ω1 близки по величине, то груз совершает колебания около положения равновесия с большой амплитудой.
б) ω=ω1 т. е. частота внешней периодической силы совпадает с частотой свободных колебаний груза. Так как iω1= iω — корень характеристического уравнения k2 + ω2 = 0, то в этом случае частное решение следует искать в виде ỹ= t(А соsωt + В sinωt.).
Дифференцируя ỹ дважды и подставляя ỹ и ỹ″ в уравнение найдем: А=  , В=0. Таким образом, ỹ = , В=0. Таким образом, ỹ = 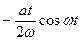 и общее решение уравнения имеет вид у= ỹ +У=А sin(ωt+φ) и общее решение уравнения имеет вид у= ỹ +У=А sin(ωt+φ) 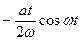
Следовательно, в данном случае имеет место сложное колебательное движение, получающееся в результате сложения двух колебаний, но с одинаковыми частотами.
Наличие множителя t во втором члене свидетельствует, что амплитуда колебаний неограниченно возрастает при неограниченном возрастании времени t, т. е. груз будет совершать через некоторый промежуток времени колебания с очень большой амплитудой, даже если амплитуда а внешней силы мала. Это явление называется резонансом. Иногда оно приводит к разрушению колеблющихся систем.
2. ВАРИАНТЫ ЗАДАНИЙ
| №
варианта
| Задание
| |
| 1.Применение дифференциальных уравнений первого порядка для решения задач динамики.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Катер движется в спокойной воде со скоростью v = 10 м/с. На полном ходу его мотор выключается и за 2 с скорость катера уменьшилась до v1=8 м/с. Сопротивление воды пропорционально скорости движения катера. Построить график изменения скорости катера в зависимости от времени.
| |
| 1.Применение дифференциальных уравнений для решения прямой задачи динамики материальной точки.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Определить силу сопротивления воды движению лодки массы m, если ее движение происходит согласно уравнению х =  , где v 0 = 10 м/с — начальная скорость движения, а — постоянный коэффициент. Сила сопротивления движению является функцией только скорости лодки. За первые 2 с движения скорость лодки изменилась до 8 м/с. Построить график изменения скорости лодки в зависимости от времени. , где v 0 = 10 м/с — начальная скорость движения, а — постоянный коэффициент. Сила сопротивления движению является функцией только скорости лодки. За первые 2 с движения скорость лодки изменилась до 8 м/с. Построить график изменения скорости лодки в зависимости от времени.
| |
| 1.Применение дифференциальных уравнений для решения обратной задачи динамики материальной точки, определение условий, обеспечивающих ее прямолинейное движение.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
В результате полученного толчка кирпич начал скользить вниз с начальной скоростью v0 = 2 м/с по неподвижной ленте конвейера, расположенной под углом α= 30° к горизонту.
Определить путь s, пройденный кирпичом за промежуток времени t=2 с, если коэффициент трения скольжения кирпича о ленту конвейера равен μ= 0,4. Кирпич считать материальной точкой.
| |
| 1.Применение дифференциальных уравнений для описания свободных колебаний.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Груз весом Р=98 Н подвешен к концу пружины, находившейся в начальный момент в покое в недеформированном состоянии, и отпущен без толчка.
Найти уравнение колебаний груза и построить график его движения, если известно, что для деформации пружины на 1 см надо приложить к ней силу, модуль которой равен 14,4 Н.
| |
| 1.Применение дифференциальных уравнений для описания вынужденных колебаний.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Определить уравнение движения материальной точки М весом Р = 196 г, движущейся вдоль оси х под действием силы упругости F и возмущающей силы S. Проекции этих сил на ось х равны: Fх=—сх, Sх=Н·sin tр, где с=2 кг/см, Н = 1,6 кг, р = 101 с-1. В начальный момент точка находилась в покое в начале отсчета на оси х. Силой сопротивления движению пренебречь.
| |
| 1.Применение дифференциальных уравнений первого порядка для решения задач динамики.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Пуля входит в брус со скоростью 200 м/с. Сила сопротивления бруса движению пули пропорциональна квадрату ее скорости. За 2 с движения скорость пули изменилась до 140 м/с. Построить график изменения скорости пули в зависимости от времени.
| |
| 1.Применение дифференциальных уравнений для решения прямой задачи динамики материальной точки, описание движения материальной точки по наклонной плоскости.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Вагонетка весом Р=100 кг канатной подвесной дороги движется вверх под углом α=300 к горизонту. Определить натяжение троса при пуске вагонетки в ход и при ее последующем равномерном движении, если пуск в ход осуществляется равноускоренно из состояния покоя в течение Т секунд. К концу пускового периода вагонетка приобрела скорость v. На вагонетку действует сила сопротивления Fс = fN, где N – модуль нормального давления вагонетки на канат, а f=0,01— постоянный коэффициент. Прогибом троса пренебречь. Построить график изменения скорости движения вагонетки.
| |
| 1.Применение дифференциальных уравнений для решения обратной задачи динамики материальной точки.
2. С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Груз весом Р=2 Н, находившийся в покое на гладкой горизонтальной плоскости, начинает двигаться под действием горизонтальной силы, проекция которой на направленную по горизонтали направо ось х равна Fх=Н·sin kt, где Н=2 и k—постоянные величины. Найти закон движения груза.
| |
| 1.Применение дифференциальных уравнений для описания свободных колебаний.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Под действием груза, подвешенного к концу пружины, пружина получила статическое удлинение Δст= 5 см.
Найти закон колебаний этого груза на пружине, если в начальный момент грузу, находившемуся в положении статического равновесия, была сообщена вверх начальная скорость v0=20 см/с.
| |
| 1.Применение дифференциальных уравнений первого порядка для решения задач теплотехники.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Температура вынутого из печи тела в течение 20 мин. падает от 200 °С до 150°С.
Температура воздуха равна 25°С. Построить график зависимости температуры тела от времени?
| |
| 1.Применение дифференциальных уравнений для решения прямой задачи динамики материальной точки.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Определить натяжение нити математического маятника длиной ℓ=2 м и весом Р=1 Н, если качания маятника совершаются согласно уравнению φ=φ0·sin kt (φ0=300 — угол отклонения маятника от вертикали, k =2). Построить график изменения скорости движения маятника.
| |
| 1.Применение дифференциальных уравнений для решения обратной задачи динамики материальной точки, описание движения тела, брошенного под углом к горизонту.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Тело брошено под углом α = 450 к горизонту с начальной скоростью v0 = 10 м/с. Найти уравнение движения тела. Построить график его движения
| |
| 1.Применение дифференциальных уравнений для описания свободных колебаний.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Найти уравнение свободных вертикальных колебаний судна весом Р=5000Н в спокойной воде. Площадь его сечения на уровне свободной поверхности воды считать не зависящей от колебаний и равной S=100м2. В начальный момент центру тяжести С, находившемуся в положении статического равновесия, была сообщена вертикально вниз скорость v0= 1м/с. Вязкостью воды пренебречь. Плотность воды γ = 1000 кг/м3.
| |
| 1.Применение дифференциальных уравнений для решения обратной задачи динамики материальной точки, движение тела под углом к горизонту с учетом сил сопротивления.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Тело брошено под углом α = 300 к горизонту с начальной скоростью v0 = 20 м/с.
Найти уравнение движения тела. Построить график его движения, если сила сопротивления пропорциональна скорости движения R = –kmv. Масса тела m=2 кг,
k – постоянный коэффициент, равный 0,01.
| |
| 1.Применение дифференциальных уравнений для описания свободных колебаний.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Груз весом Р = 9,8 Н лежит на гладкой горизонтальной плоскости. Слева и справа он соединен с концами двух горизонтально расположенных пружин (см. рисунок) с коэффициентами упругости с1 = 4 н/см, с2 = 5 н/см. В положении равновесия груза обе пружины недеформированы.
 Найти уравнение движения и период колебаний груза, если в начальный момент он был смещен из положения равновесия направо на 4 см и ему была сообщена направо начальная скорость 90 см/сек. Найти уравнение движения и период колебаний груза, если в начальный момент он был смещен из положения равновесия направо на 4 см и ему была сообщена направо начальная скорость 90 см/сек.
| |
| 1.Применение дифференциальных уравнений для решения обратной задачи динамики материальной точки.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Измерение глубины реки производится с помощью груза, опускаемого на тросе в воду до дна реки. При опускании груза со скоростью v0 трос оборвался и груз достиг дна через Т секунд после момента обрыва троса.
Определить путь Н, пройденный грузом до дна реки, если проекция на ось х силы сопротивления воды движению груза равна
 где m — масса груза, х' — проекция его скорости на ось х, k—постоянный коэффициент. Ось х направлена по вертикали вниз. Силой выталкивания груза из воды пренебречь. где m — масса груза, х' — проекция его скорости на ось х, k—постоянный коэффициент. Ось х направлена по вертикали вниз. Силой выталкивания груза из воды пренебречь.
| |
| 1.Применение дифференциальных уравнений для описания свободных колебаний.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Груз весом Р = 98 Н, подвешенный к концу пружины, движется в жидкости. Коэффициент жесткости пружины с=10 Н/см. Сила сопротивления движению пропорциональна первой степени скорости груза: R=βv, где β=1,6 нс/см.
Найти уравнение движения груза, если в начальный момент груз был смешен из положения статического равновесия вниз на 4 см и ему была сообщена вниз начальная скорость v0 = 4 см/с.
| |
| 1.Применение дифференциальных уравнений для описания свободных колебаний.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Составить дифференциальное уравнение свободных гармонических колебаний грузового блока весом 1 т, если колебания возникли в результате удара волны о борт (периодической силы) амплитудой 0,5 м и частотой π/12, без учета сопротивления. Жесткость троса принять равной 1 Н/см.
| |
| 1.Применение дифференциальных уравнений для описания свободных колебаний.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Составить дифференциальное уравнение задачи «погони». Судно движется равномерно (вдоль оси х) с постоянной скоростью 15 узлов, его преследует катер движущийся с постоянной скоростью 25 узлов по кратчайшей траектории к направлению движения судна. Найти уравнение и траекторию движения судна, координату точки их встречи и продолжительность погони.
| |
| 1.Применение дифференциальных уравнений для описания свободных колебаний.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Составить дифференциальное уравнение задачи «погони». Судно движется равномерно (вдоль оси х) с постоянной скоростью 15 узлов, его преследует катер движущийся с постоянной скоростью 25 узлов по кратчайшей траектории к направлению движения судна. Найти уравнение и траекторию движения судна, координату точки их встречи и продолжительность погони.
| |
| 1.Применение дифференциальных уравнений первого порядка для решения задач динамики.
2.С помощью дифференциального уравнения решить следующую задачу, построить интегральную кривую.
Составить дифференциальное уравнение свободных гармонических колебаний грузового блока весом 1 т, если колебания возникли в результате удара волны о борт (периодической силы) амплитудой 0,5 м и частотой π/12, без учета сопротивления. Жесткость троса принять равной 1 Н/см.
| Рекомендуемая литература:
1. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 1988.
2. Дубовик В.П., Юрик І.І. Вища математика. - К.: Видавництво А.С.К., 2003.
3. Пискунов Н.С. Дифференциальное и интегральное исчисления. – М.: Наука, 1978. – Том 1.
4. Письменный Д.Т. Конспект лекций по высшей математике.-М.: «Айрис-пресс», 2007
5. Смирнов В.И. Курс высшей математики. — М.: Наука, 1974.
6. Шипачев В.С., Высшая математика.-М.: «Высшая школа», 2006
7. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. — т. 2,3 М.: Наука, 1966.
|



 , mу" =
, mу" =  , mz" =
, mz" =  .
. ,
,  =
= 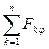
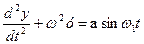
 , А=0.
, А=0. , В=0. Таким образом, ỹ =
, В=0. Таким образом, ỹ = 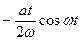 и общее решение уравнения имеет вид у= ỹ +У=А sin(ωt+φ)
и общее решение уравнения имеет вид у= ỹ +У=А sin(ωt+φ)  , где v 0 = 10 м/с — начальная скорость движения, а — постоянный коэффициент. Сила сопротивления движению является функцией только скорости лодки. За первые 2 с движения скорость лодки изменилась до 8 м/с. Построить график изменения скорости лодки в зависимости от времени.
, где v 0 = 10 м/с — начальная скорость движения, а — постоянный коэффициент. Сила сопротивления движению является функцией только скорости лодки. За первые 2 с движения скорость лодки изменилась до 8 м/с. Построить график изменения скорости лодки в зависимости от времени.
 Найти уравнение движения и период колебаний груза, если в начальный момент он был смещен из положения равновесия направо на 4 см и ему была сообщена направо начальная скорость 90 см/сек.
Найти уравнение движения и период колебаний груза, если в начальный момент он был смещен из положения равновесия направо на 4 см и ему была сообщена направо начальная скорость 90 см/сек.
 где m — масса груза, х' — проекция его скорости на ось х, k—постоянный коэффициент. Ось х направлена по вертикали вниз. Силой выталкивания груза из воды пренебречь.
где m — масса груза, х' — проекция его скорости на ось х, k—постоянный коэффициент. Ось х направлена по вертикали вниз. Силой выталкивания груза из воды пренебречь.



