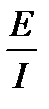Непосредственные силлогизмы, правдоподобные и неправдоподоб-ные умозаключения по логическому квадрату

Выше мы выделили и описали четыре вида отношений между множественными суждениями вида А, Е, I, О в логическом квадрате:

1) отношение подчинения

2) отношение субконтрарности

3) отношение контрарности

4) отношение контрадикторности

Поскольку каждое из этих отношений является бинарным, т.е. связывает два суждения, и эти суждения являются сравнимыми по содержанию, постольку, беря одно из суждений в качестве посылки, мы имеем все основания рассматривать другое суждение, находящееся с первым в одном из четырех отношений, в качестве заключения однопосылочного ПКУ. Далее, учитывая истинностные значения суждений, находящихся в одном из четырёх выделенных в ЛК отношений, мы можем описать все возможные непосредственные силлогизмы (дедуктивные умозаключения) по каждому из выделенных отношений и в конечном счете по всему логическому квадрату.

1) Непосредственные силлогизмы и правдоподобные умозаключения, отношения подчинения.

Из описания отношений между суждениями по истинностным значениям в логическом квадрате мы уже знаем, что из истинности подчиняющих суждений (А, Е) с необходимостью дедуктивно следует истинность подчиненных суждений (I, О). Данное дедуктивное следование опирается на следующую аксиоматику:

1) если некоторый признак-свойство присущ каждому элементу объёма понятия, стоящего на месте S в суждениях вида А, то он с необходимостью присущ любой части объема понятия, стоящего на месте S в суждении вида I;

2) если признак-свойство не присущ каждому элементу объема понятия, стоящего на месте субъекта S в суждении вида Е, то он с необходимостью не присущ и любой части объема понятия, стоящего на месте субъекта S в суждении вида О.

Данная аксиоматика объясняет дедуктивность и силлогистичность следующих непосредственных умозаключений отношения подчинения вида:

 

а)

б)

Но в ЛК являются непосредственными силлогизмами отношения подчинения также умозаключения вида:

 

в)

г)

 

Их дедуктивность и, следовательно, силлогистичность обосновывается опосредованным способом, т.е. с учетом свойств отрицания суждений, входящих в ЛК.

Рассмотрим умозаключение вида в). Понятно, что для обоснования дедуктивности и силлогистичности этого умозаключения нужно допустить истинность I, т.е. истинность суждения с логической формой «Неверно, что некоторые S есть Р». Как известно из ЛК, суждение данного вида равнозначно истинному суждению вида Е: «Ни один S не есть Р», которое находится в отношении контрарности с суждением вида А. Тогда на основании свойств отношения контрарности (суждения, находящиеся в отношении контрарности, т.е. А, Е, не могут быть вместе истинными, но могут быть вместе ложными) и того, что Е является истинным, следует, что А является ложным. Но тогда отрицание А, т.е. А, примет значение «истина». Таким образом, в умозаключении вида в) мы с логической необходимостью переходим от истинной посылки к истинному заключению, т.е. умозаключение вида в) является дедуктивным и силлогистичным.

Аналогичная ситуация имеет место для умозаключения вида г). Допустим, что суждение вида О является истинным суждением. Тогда равнозначное ему суждение А также будет истинным, а суждение вида Е, находящееся с ним в отношении контрарности, примет значение «ложь». Но отсюда следует, что отрицание суждения вида Е, т.е. суждение вида Е, примет значение «истина». Таким образом, в умозаключении вида г) мы также с логической необходимостью переходим от истинной посылки к истинному заключению, что свидетельствует о его дедуктивности и силлогистичности.

Примеры[37]:

а) А: Все студенты есть учащиеся. – И

I: Некоторые студенты есть учащиеся. – И

б) Е: Ни один треугольник не есть квадрат. – И

О: Некоторые треугольники не есть квадраты. – И

в) I: Неверно, что некоторые треугольники есть квадраты. – И

А: Неверно, что все треугольники есть квадраты. – И

г) О: Неверно, что некоторые квадраты не есть ромбы. – И

Е: Неверно, что все квадраты не есть ромбы. – И

Интуитивно ясно, что следующие непосредственные умозаключения отношения подчинения представляют недедуктивные правдоподобные умозаключения:

д)

е)

Примеры[38]:

д) I: Некоторые жильцы нашего дома имеют вклады в банках. – И

А: Все жильцы нашего дома имеют вклады в банках. – И

 

е) О: Некоторые жильцы нашего дома не были в Риме. – И

Е: Все жильцы нашего дома не были в Риме. – И

 

2) Непосредственные силлогизмы и правдоподобные умозаключения отношения субконтрарности.

В отношении субконтрарности в ЛК находятся суждения вида I,О.

К числу непосредственных силлогизмов отношения субконтрарности относятся умозаключения вида: а) I б) О

 

О I

Обоснование их силлогистичности и дедуктивности.

Рассмотрим случай а). Допустим, что суждение вида I является истинным, тогда суждение вида I будет ложным. Но суждения, находящиеся в отношении субконтрарности, т.е. суждения вида I, О, не могут быть вместе ложными. Отсюда следует, что при ложности I суждение вида О с необходимостью будет истинным. Таким образом, в умозаключениях вида а) с логической необходимостью осуществляется переход от истинной посылки I к истинному заключению вида О, что свидетельствует о силлогистичности и дедуктивности умозаключения данного вида.

Рассмотрим случай б). Допустим, что суждение вида О истинно, тогда суждение О примет значение «ложь», но так как О и I не могут быть вместе ложными, то при ложности суждения вида О суждение вида I примет значение «истина».

Итак, в умозаключениях вида б) с логической необходимостью осуществляется переход от истинной посылки вида О к истинному заключению вида I.

К числу непосредственных умозаключений отношения субконтрарности следует также отнести умозаключения вида
в) I г) О д) I е) О

О I О I

Рассмотрим умозаключения вида в). Допустим, что посылка I является истинным суждением. Тогда заключение О может оказаться как истинным, так и ложным суждением, так как суждения I, О в ЛК не могут быть вместе ложными, но могут быть вместе истинными. Таким образом, в умозаключении вида в) при истинности посылки I не исключается истинность заключения О, что в соответствии с определением правдоподобного следования на качественном уровне (см. 4.2. Понятие о логическом следовании (о логичности рассуждения в §4 Главы 1) позволяет отнести умозаключение вида в) к числу недедуктивных правдоподобных умозаключений.

Пример. I: Некоторые студенты знают логику – И,

Правдоподобно следует, что О: Некоторые студенты не знают логику. – И, Л

Рассмотрим умозаключение вида г).

Допустим, что посылка О является истинным суждением, тогда заключение I может оказаться как истинным, так и ложным, ведь суждения I,О не могут быть вместе ложными, но могут быть вместе истинными. Таким образом, умозаключения вида г) можно отнести к числу недедуктивных правдоподобных умозаключений.

Пример. О: Некоторые студенты не знают логику – И,

Правдоподобно следует, что I: Некоторые студенты знают логику. – И, Л

Рассмотрим умозаключение вида д ). Допустим, что посылка I является истинной. Тогда суждение вида О может оказаться как истинным, так и ложным, поскольку О, I в ЛК не могут быть вместе ложными, но могут быть вместе истинными; но отрицание О, т.е. суждение вида О, также может оказаться как истинным, так и ложным, ведь отрицание истинного суждения О даст ложное суждение вида О, а отрицание ложного суждения О даст истинное суждение О.

Это значит, что в соответствии с определением правдоподобного следования на качественном уровне (см. 4.2. §4 Главы 1) умозаключение вида д) является недедуктивным правдоподобным умозаключением.

Пример. I: Некоторые студенты знают логику – И,

Правдоподобно следует, что О: Неверно, что некоторые студенты не знают логику. – И, Л

Рассмотрим умозаключение вида е).

Допустим, что посылка О является истинной, тогда суждение вида I может оказаться как истинным, так и ложным, потому что I, О в ЛК не могут быть вместе ложными, но могут быть вместе истинными. Такая же ситуация сохранится и для суждения вида I, что в конечном счете приводит к выводу, что умозаключение вида е) также является недедуктивным правдоподобным умозаключением.

Пример. О: некоторые студенты не знают логику – И,

Правдоподобно следует, что I: Неверно, что некоторые студенты знают логику. – И, Л

3) Непосредственные силлогизмы и правдоподобные умозаключения отношения контрарности.

В отношениях контрарности в ЛК находятся суждения А, Е. К числу непосредственных силлогизмов отношения контрарности относятся умозаключения:

а) А б) Е

Е А

Обоснование силлогистичности и дедуктивности умозаключения вида а).

Допустим, что суждение вида А истинно. Так как суждения, находящиеся в отношении контрарности, не могут быть вместе истинными, но могут быть вместе ложными, то при истинности посылки А суждение Е с логической необходимостью будет ложным. В этой ситуации очевидно, что для получения силлогистичного умозаключения в отношении контрарности с истинной посылкой А необходимо взять ложное суждение Е под отрицание. В результате получим истинное суждение - заключение вида Е.

Обоснование силлогистичности и дедуктивности умозаключения вида б).

Оно аналогично обоснованию силлогистичности и дедуктивности умозаключения вида а). Предлагаем читателю самостоятельно осуществить данную процедуру.

 

Содержательные примеры непосредственных силлогизмов:

Пример для а):

А: Все липы есть деревья. – И

Е: Неверно, что ни одна липа не есть дерево. – И

Пример для б):

Е: Ни один треугольник не есть квадрат. – И

А: Неверно, что все треугольники есть квадраты. – И

К числу недедуктивных правдоподобных умозаключений отношения контрарности относятся умозаключения вида

в) А г) Е

Е А

Обоснование правдоподобности непосредственных умозаключений вида в).

Допустим, что суждение - посылка вида А является истинной. Тогда суждение А, входящее в посылку, будет ложным. Так как в ЛК суждения, находящиеся в отношении контрарности, не могут быть вместе истинными, но могут быть вместе ложными, то при ложности суждения А суждение Е может быть как истинным, так и ложным. Это значит, что в заключении не исключается случай истинности суждения Е, что соответствует определению правдоподобного следования на качественном уровне в контексте умозаключения. Следовательно, в умозаключениях вида в) посылка и заключение связаны между собой отношением правдоподобного следования, в силу чего само умозаключение вида в) квалифицируется как недедуктивное правдоподобное умозаключение.

Содержательный пример правдоподобного умозаключения в)[39].

А: Неверно, что все карандаши, лежащие на этом столе, красные – И,

Е: Все карандаши, лежащие на этом столе, не есть красные. – И, Л

 

Обоснование правдоподобности непосредственных умозаключений вида г) аналогично обоснованию правдоподобности умозаключений вида в). Читателю предоставляется возможность самому убедиться в этом.

Содержательный пример правдоподобного умозаключения вида г)[40].

Е: Неверно, что все карандаши, лежащие на этом столе, некрасные. – И,

А: Все карандаши, лежащие на этом столе, – красные. – И, Л

Выше мы привели содержательные примеры недедуктивных правдоподобных умозаключений, в которых суждения А, Е, а также Е, А относятся к категории фактофиксирующих (случайно истинных/ложных суждений).

Когда же эти суждения относятся к категории необходимо истинных/ложных суждений, то здесь, на наш взгляд, просматривается ситуация обнаружения недедуктивных неправдоподобных умозаключений.

Пример 1. А: Неверно, что все лебеди белые – И,

Е: Ни один лебедь не бел. – Л

Пример 2. Е: Неверно, что ни одно четное число не является простым – И,

А: Все четные числа являются простыми. – Л

 

4) Непосредственные силлогизмы и неправдоподобные умозаключения отношения контрадикторности.

При выделении непосредственных силлогизмов отношения контрадикторности будем исходить из предпосылки, что суждения, находящиеся в отношении контрадикторности (А, О, Е, I), не могут быть вместе истинными и не могут быть вместе ложными: при истинности одного из них другое обязательно (необходимо) будет ложным и, наоборот, при ложности одного из них другое с необходимостью будет истинным (см. «Логический квадрат», с.109).

Отсюда следует, что если выбрать в качестве посылки истинное суждение отношения контрадикторности, то другое суждение этого отношения, которое примет статус заключения непосредственного умозаключения отношения контрадикторности, окажется необходимо ложным, т.е. мы получим недедуктивное неправдоподобное умозаключение, так как посылки и заключения в данной ситуации будут находиться между собой в отношении противоречия.

Данная ситуация подсказывает следующие два способа выделения всех непосредственных силлогизмов отношения контрадикторности:

Первый способ. Подвергнуть отрицанию суждения, входящие в посылки. Тогда если эти суждения были ложными, то их отрицание даст истинную посылку при истинном заключении, т. е. данная логическая форма умозаключения обеспечит необходимый переход от истинной посылки к истинному заключению, и, следовательно, данное умозаключение будет дедуктивным и силлогистичным. Если же эти суждения были истинными, то их отрицание даст ложные посылки, а из лжи, как мы уже знаем, следует все что угодно, т.е. и в данной ситуации также с необходимостью выполняется условие дедуктивности и силлогистичности умозаключения. В итоге на данном пути мы получим следующие виды непосредственных силлогизмов отношения контрадикторности:

а)

б)

в)

г)

Второй способ. Подвергнуть отрицанию суждения, которые займут место заключения в непосредственном умозаключении отношения контрадикторности. Тогда при истинных посылках мы с необходимостью придем к истинным заключениям, так как в силу отношений между суждениями A, O, E, I по истинностным значениям в логическом квадрате мы подвергнем отрицанию ложные суждения, стоящие в заключении, и, следовательно, выполним условие дедуктивности и силлогистичности умозаключений данного вида. Если же посылка будет ложной, то очевидно, что отношение дедуктивного следования между посылкой и заключением в данной ситуации также сохраняется. В итоге на втором пути мы получим также четыре вида непосредственных силлогизмов:

а)

б)

в)

г)

Таким образом, по всем отношениям между суждениями вида A, E, I, O мы получим 16 непосредственных силлогизмов по логическому квадрату. Читателю предлагается самостоятельно убедиться, что непосредственные умозаключения вида:

 

будут представлять недедуктивные неправдоподобные и тем самым нелогичные умозаключения.