
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила выводов логики суждений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Существует группа дедуктивных умозаключений, для логического анализа которых достаточно рассматривать входящие в них суждения как не расчлененные на части (на субъект и предикат), т.е. без учета внутренней структуры этих суждений. Такие умозаключения строятся с учетом логических связей между отдельными суждениями. Они называются выводами логики суждений (высказываний). Правила выводов логики суждений подразделяются на основные и производные. Основные правила являются более простыми. Их перечень составляется так, чтобы, во-первых, правила были содержательно очевидными и, во-вторых, образованная из них система удовлетворяла требованию полноты, т.е. определяла все возможные правила выводов логики суждений. Производные правила выводятся из основных правил. Как основные, так и производные правила, в свою очередь, делятся на прямые и непрямые (косвенные). Прямые правила указывают на выводимость одних суждений из других суждений (заключений — из посылок). Непрямые правила дают возможность заключить о правомерности некоторых выводов на основании правомерности других выводов.
Прямые правила: А 1. Правило введения конъюнкции (ВК) — В. А Ù В
А Ù В.; А Ù В. 2. Правило удаления конъюнкции (УК) — А В
3. Правило введения дизъюнкции (ВД) — А; В. А Ú В А Ú В
4. Правило удаления дизъюнкции (УД) —
А É В 5. Правило удаления импликации (УИ) — А. В
6. Правило введения эквиваленции (ВЭ) — А É В В É А А «В
7. Правило удаления эквиваленции (УЭ) — А «В А É В В É А
8. Правило введения двойного отрицания (ВДО) — А
9. Правило удаления двойного отрицания (УДО) — А
Непрямые правила: 1. Правило введения импликации (ВИ) —
П (посылки)
А (добавочное допущение) : : В.
А É В
(При записи ВИ и некоторых других правил мы будем использовать квадратные “горизонтальные” скобки, в которых для получения вывода помещаются добавочные допущения и следствия из них. Находящиеся в этих скобках выражения выполняют, образно говоря, роль строительных лесов, которые можно убрать после построения вывода). Правило ВИ устанавливает, что если на основании посылок П и добавочного допущения А мы получим суждение В качестве следствия, то можно заключить о выводимости из П импликации А É В; 2. Правило сведения “к абсурду” (СА) —
П (посылки)
А (добавочное допущение) : :
Правило СА устанавливает, что если при посылках П и добавочном допущении А в процессе вывода получаются два противоречащих друг другу суждения В и С помощью названных основных правил можно вывести все производные правила. Например, так называемое правило условного силлогизма
А É В В É С АÉ С
выводится так: 1. А É В (посылка) 2. В É С (посылка) 3. А (добавочное допущение) 4. В (УИ: 1,3) 5. С (УИ: 2,4) 6. А É С (ВИ: 1, 5) Выражения в скобках указывают, на основании каких правил и строк вывода получено то или иное следствие. Например, выражение (УИ: 1,3) означает, что следствие, находящееся слева от данного выражения, получено на основании применения правила УИ к строкам 1 и 3. При обосновании производных правил вывода весьма удобным приемом является так называемый способ рассуждения “от противного”. Он состоит в том, что к посылкам в качестве добавочного допущения приписывается отрицание заключения и по правилам выводов находятся следствия. Если в процессе рассуждения мы приходим “к абсурду”, то допущение признается ложным, а, следовательно, заключение является истинным. Правила выводов тесно связаны с логическими законами. Всегда можно сформулировать логический закон, соответствующий тому или иному правилу вывода. Так, правило, по которому на основании посылки “Если сегодня суббота, то завтра воскресенье” получено заключение “Если неверно, что завтра воскресенье, то неверно, что сегодня суббота”, можно сформулировать следующим образом: “Из суждения вида А É В можно выводить суждения вида
|
||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 845; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.36 (0.006 с.) |

 ;
; 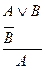


 , то данное допущение должно быть отвергнуто и признано, что из П выводимо отрицание допущения —
, то данное допущение должно быть отвергнуто и признано, что из П выводимо отрицание допущения — 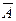 .
.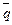 É
É  ).
).


