Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Язык и правила выводов логики предикатов.Содержание книги
Поиск на нашем сайте
На языке логики предикатов можно выражать логические схемы, в которых отображается внутренняя структура суждений. В этом языке используются следующие семантические категории: а) все семантические категории, используемые при построении языка логики высказываний (пропозициональные переменные, вместо которых можно подставлять высказывания с конкретным содержанием, и функторы, способные к порождению из одних высказываний других, более сложных высказываний; б) пропозициональные функции вида P(x), Q(x), R(x,y),R(x,y,z) и т.п. (предикаты), где P, Q, R обозначают свойства предметов или отношение между ними, а x, y, z,... — именные переменные (следует обратить внимание на то, что здесь термин “предикат” определен иначе, чем в традиционной логике); в) имена предметов а, в, с,..., которые можно подставить вместо переменных x, y, z,...; г) кванторы: общности " и существования $. Используя эти категории, можно составить различные выражения. Например, выражение " xP(x), которое читается: “Для всякого х верно, что х имеет свойство Р” (сокращенно: “Для всякого х: Р от х”), — и является схемой произвольного суждения, гласящего, что все предметы какого-то класса обладают свойством Р; выражение $ хР(х), которое читается: “Существует предмет, обладающий свойством Р” (сокращенно: “Существует х: Р от х”, — и является схемой произвольного суждения, гласящего, что существует предмет (хотя бы один), который имеет свойство Р; выражение " х $ уР(х,у), которое является схемой произвольного суждения, гласящего, что всякий предмет находится в отношении Р к некоторому предмету у (сокращенно читается: “Для всякого х существует у: Р от х и у”). Предикат, не расчлененный на другие предикаты, называется элементарным. Приписывание к предикату квантора общности или существования называется операцией связывания квантором. Операция связывания квантором является одним из способов образования суждения из предиката. Вторым способом является подстановка вместо переменных их значений (постоянных). Правильная подстановка, т.е. такая, в результате которой из истинных выражений получаются только истинные выражения, требует соблюдения определенных правил. Правила подстановки для логики предикатов первой ступени, где в качестве переменных могут выступать лишь именные переменные, следующие:
1. Подставляемые выражения должны принадлежать к той же предметной области, на которой определена переменная х; 2. Подстановка значений вместо переменной х возможна лишь там, где переменная свободна; 3. Если мы прибегаем к подстановке некоторого значения вместо переменной х, то подстановка осуществляется везде, где встречается х в данном выражении; 4. В результате подстановки ни одна свободная переменная не должна оказаться связанной. К основным правилам выводов логики предикатов относятся все основные правила выводов логики суждений, а также правила удаления и введения кванторов. Правила для выражений логики предикатов с одной переменной следующие: Правило удаления квантора общности: если имеется выражение вида "aF, то из него можно выводить выражение вида F’, получающееся из F путем подстановки вместо переменной a постоянной или произвольной переменной. Правило введения квантора общности: если в выводе имеется выражение вида F, то можно выводить выражение вида "a F, с условием, что переменная a является связанной в посылках и допущениях. Правило удаления квантора существования: если в выводе имеется выражение вида $aF, то можно выводить выражение вида F ’, получающееся из F путем подстановки вместо переменной a некоторой постоянной, не встречавшейся ни в одной из строк вывода. Правило введения квантора существования: если в выводе имеется выражение вида F, то можно выводить выражение вида $aF ’, в котором F ’ получается из F путем подстановки вместо постоянной или переменной (везде, где она свободна) переменной a, с условием, что переменная a является связанной в посылках и допущениях. 5. Выводы посредством преобразования суждений. В традиционной логике рассматриваются так называемые непосредственные умозаключения, или выводы посредством преобразования суждений. К ним относятся: превращение, обращение, противопоставление предикату, выводы из отношений между суждениями, или выводы по логическому квадрату. Характерной особенностью этих умозаключений является наличие одной посылки. Превращением называется преобразование суждения в суждение, противоположное по качеству с предикатом, противоречащим предикату исходного суждения.
Чтобы превратить суждение, нужно изменить его связку на противоположную, а предикат — на противоречащее понятие. Схемы превращения: (А) Все S суть Р (Е) Ни одно S не есть Р (Е) Ни одно S не есть не-Р (А) Все S суть не-Р
(I) Некоторые S суть Р (О) Некоторые S не суть Р (О) Некоторые S не суть не-Р (I) Некоторые S суть не-Р
Обращением называется преобразование суждения, в результате которого субъект исходного суждения становится предикатом, а предикат — субъектом заключения. Схемы обращения: (А) Все S суть Р (Е) Ни одно S не есть Р (I) Некоторые Р суть S (E) Ни одно Р не есть S
(I) Некоторые S суть Р (I) Некоторые Р суть S
Частноотрицательные суждения (О) не обращаются. Противопоставлением предикату называется преобразование суждения в результате которого субъектом становится понятие, противоречащее предикату, а предикатом — субъект исходного суждения. Схемы противопоставления предикату: (А) Все S суть Р (Е) Ни одно S не есть Р. (Е) Ни одно не-Р не есть S (I) Некоторые не-Р суть S
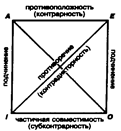
(О) Некоторые S не суть Р (I) Некоторые не-Р суть S Частноутвердительное суждение (I) путем противопоставления предикату не преобразуется. Противопоставление предикату может быть рассмотрено как результат двух последовательных операций: превращения и обращения. Умозаключения по логическому квадрату. Простые сравнимые суждения, имеющие одинаковые термины и различающиеся по качеству и количеству, находятся в определенных отношениях, которые иллюстрируются с помощью логической схемы (логического квадрата).
Опираясь на логический квадрат, можно строить выводы, устанавливая следование истинности или ложности одного суждения из истинности или ложности другого суждения в зависимости от свойств отношений. Отношение противоречия (контрадикторности): A—O, E—I. Эти суждения не могут быть одновременно ни истинными, ни ложными. Из истинности одного суждения следует ложность другого суждения, из ложности одного — истинность другого. Выводы строятся по схемам: Аи ® Ол; Ал ® Ои; Еи ® Iл; Ел ® Iи. Отнош ение противоположности (контрарности): А — Е. Противоположные суждения не могут быть одновременно истинными, но могут быть одновременно ложными. Из истинности одного суждения следует ложность другого, но из ложности одного из них может следовать как истинность, так и ложность другого суждения. Выводы строятся по схемам: Аи ® Ел; Еи ® Ал; Ал ® Е?; Ел® А? Отношение частичной совместимости (субконтрарности): I — O. Эти суждения могут быть одновременно истинными, но не могут быть одновременно ложными. Из ложности одного суждения следует истинность другого, но из истинности одного из них может следовать как истинность, так и ложность другого. Выводы строятся по схемам: Iл ® Oи; Oл ® Iи; Iи ® O?; Ои ® I? Отношения подчинения: А—I, Е—О. Из истинности подчиняющего суждения следует истинность подчиненного суждения, но не наоборот: из истинности подчиненного суждения истинность подчиняющего суждения не следует, оно может быть истинным, но может быть ложным. Выводы строятся по схемам: Aи ® Iи; Eи ® Oи; Iи ®?; Ои ®? Из ложности подчиненного суждения следует ложность подчиняющего суждения, но не наоборот: из ложности подчиняющего суждения ложность подчиненного суждения с необходимостью не следует, оно может быть истинным, но может быть и ложным. Выводы строятся по схемам: Iл ® Aл; Oл ® Eл; Aл ®?; Eл ®?
|
|||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.255.227 (0.009 с.) |