
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о формализованном языке. Семантические категории.Содержание книги
Поиск на нашем сайте
Логика Материалы к курсу Евпатория 2013 ☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺ Тема 1. Предмет формальной логики. Понятие о логической форме. Логика изучает формы или структуры мыслей, отвлекаясь от их конкретного содержания. Для уяснения этого положения рассмотрим несколько примеров. Пусть у нас имеются несколько утверждений: “Все квадраты - прямоугольники”, “Все птицы - позвоночные”. Легко заметить, что эти мысли по своему конкретному содержанию отличаются друг от друга. Но вместе с тем они обладают чем-то общим. А именно, в них зафиксировано наличие у объектов (в данном случае у квадратов и птиц) соответствующих признаков (того, что они прямоугольники или позвоночные) и эти признаки выражаются с помощью одинаково расположенных общих для этих выражений слов — “все” и “суть” (в наших примерах слово “суть” заменено тире). Обозначим все части предложений, находящиеся между словами “все” и “суть”, буквой А. Те же, которые расположены после “суть”, буквой В. Получается общая схема построения этих мыслей. Она имеет следующую логическую форму: “Все А суть В”. Таким образом, видно, что общее характеризуется не конкретным содержанием этих мыслей и утверждений, а способом их построения, или логической формой. Теперь рассмотрим более сложные примеры: “Если по данному проводнику протекает электрический ток, то вокруг него образуется магнитное поле. Следовательно, если вокруг проводника не образуется магнитное поле, то по проводнику не проходит электрический ток”. “Если число делится на 2 и 3, то оно делится на 6. Следовательно, если число не делится на 6, то оно не делится на 2 и 3”. Как и вышеприведенные более простые примеры эти контексты отличаются друг от друга конкретным содержанием. Но есть и нечто общее, объединяющее их. Это общее заключается в том, что здесь мы путем преобразования одних мыслей получаем какие-то новые мысли. Это новое знание получается с помощью схемы или логической формы. Для более четкого понимания разобьем данные контексты на простые высказывания и обозначим их, как это принято в логике, маленькими буквами из середины латинского алфавита. Для первого контекста этими высказываниями будут: “По данному проводнику протекает электрический ток” и “Вокруг него образуется магнитное поле”. Обозначим их соответственно p и q. Поставив буквы p и q в данный контекст, получим следующую логическую форму данного выражения — “Если p, то q, следовательно, если не q, то не p”. Проделав ту же операцию формализации со вторым контекстом и выделив в качестве элементарных высказываний выражения “число делится на 2 и 3” и “оно (число) делится на 6”, а также заменив соответствующие высказывания буквами латинского алфавита,, мы увидим, что второй контекст имеет ту же самую логическую форму, что и первый. А именно: “Если p, то q, следовательно, если не q, то не p”.
Таким образом, как в сложных, так и в простых выражениях можно выделить логическую форму. Она определяется в логике как сложившаяся в процессе многовековой практики структура отображения в человеческом мышлении наиболее общих, чаще всего встречающихся отношений вещей объективного мира, связей вещей и их свойств. Как и другие науки, логика пользуется словами, которые не меняют своего значения в любом контексте или рассуждении. Эти слова называются логическими постоянными. Чаще всего в качестве логических постоянных используют слова “все”, “некоторые”, “ суть”, “и”, “или”, “если..., то”, “неверно, что”, “необходимо”, “возможно” и др. Используемые в логике для обозначения выражений с различным содержанием знаки называются логическими переменными. В наших примерах это буквы А, В, p и q. Хотя можно вводить и другие знаки. Конкретное содержание выражений, замененное логическими переменными, называется значениями этих переменных. Мы использовали следующие значения переменных: “Квадраты”, “птицы”, “по данному проводнику протекает электрический ток”, “число делится на 2 и 3” и др. Множество предметов, свойств или отношений, из которого можно выбирать для переменной ее значение называется областью значений этой переменной. Выявление логической формы мысли называется ее формализацией. Для достижения четкости и строгости выражений логики выражает логические постоянные при помощи символов. “Все” обозначается знаком ", “некоторые” — $, “и” — Ù, “или” — Ú, выражение “если..., то” — É, “неверно, что” — `(черта над выражением) или ù, “необходимо” — , “возможно” — à и т.д. Впрочем, для обозначения логических постоянных, по соглашению, можно вводить и другие символы.
Предварительные сведения о логическом законе. Логическими законами называются такие структуры, при пользовании которыми мы, отталкиваясь от ранее полученного истинного знания, с неизбежностью приходим к новому, тоже истинному знанию. Эта правильность перехода от одного знания к другому при помощи логических законов обнаруживает действительные, реально существующие, объективные связи и отношения предметов внешнего мира. Для разъяснения данного положения рассмотрим следующую схему: “Некоторые А суть В, следовательно, некоторые В суть А”. Нетрудно заметить, что она отвечает требованиям правильности, т.к. при истинности утверждения “Некоторые А суть В” утверждение “Некоторые В суть А” будет истинным с необходимостью. Теперь проанализируем другую схему: “Некоторые А суть В, следовательно, все А суть В”. В данном случае из истинности утверждения “Некоторые А суть В” не следует с необходимостью истинность утверждения “Все А суть В”. Это легко видно, если вместо символов А и В в схеме поставить конкретные выражения. Так, например, из истинности утверждения “Некоторые ученые — спортсмены” не вытекает истинности утверждения “Все ученые — спортсмены”. Таким образом, видно, что в первом случае рассуждение ведется по логическим законам, во втором же рассуждение неправильно. Анализ понятия “логический закон” позволяет нам более четко представить предмет логики и определить ее как науку о закономерностях правильного мышления, т.е. такого мышления, при котором обеспечивается переход от ранее установленных истин к новому знанию без обращения в каждом конкретном случае к опыту, на основании использования мыслительных схем, сложившихся в результате многократного повторения при постижении истины. Тема 2. Понятие. Общая характеристика понятия. Содержание и объем понятия. Виды понятий. Понятие — это форма мышления, в которой обобщаются и выделяются предметы и явления того или иного класса по существенным признакам. Существенным называется такой признак, который выражает коренную природу выделяемых предметов и служит основой обобщения их в классы. Всякое понятие со стороны структуры характеризуется наличием определенного объема и содержания. Объемом понятия называется совокупность (класс) предметов, которые мыслятся в данном понятии, а содержанием — совокупность признаков, на основании которой предметы обобщаются в классы. По объему понятия делятся на единичные и общие. Единичными называются понятия, в которых отражаются классы состоящие из одного элемента (“философ Сократ”), а понятия, в которых отражаются классы, состоящие из двух и более элементов, называются общими (“философ”). Кроме этого, выделяют понятия, объемы которых представляют собой классы, не содержащие ни одного элемента (“вечный двигатель”). Такие понятия называются нулевыми или пустыми. Общие понятия могут быть регистрирующими и нерегистрирующими. Регистрирующими называются понятия, в которых множество мыслимых в нем элементов поддается учету, регистрируется (во всяком случае в принципе). Например, «участник международной конференции по физике». Регистрирующие понятия имеют конечный объем.
Общее понятие, относящееся к неопределенному числу предметов, называется нерегистрирующим. Так, в понятии «человек» множество мыслимых в нем элементов (людей) не поддается учету. Так как в понятии «человек» мыслятся все люди, которые существовали когда-либо, существуют и будут существовать. Нерегистрирующие понятия имеют бесконечный объем. В особую группу выделяются собирательные понятия, в которых мыслятся совокупности элементов, составляющих единое целое, например «коллектив», «полк», «созвездие». Эти понятия, так же как и общие, отражают множество элементов (членов коллектива, солдат и командиров полка, звезд), однако, как и в единичных понятиях, это множество мыслится как единый предмет. Содержание собирательного понятия нельзя отнести к каждому отдельному элементу, входящему в его объем, оно относится ко всей совокупности элементов. Например, существенные признаки коллектива (группа лиц, объединенных общей работой, общими интересами) неприложимы к каждому отдельному члену коллектива. Собирательные понятия могут быть общими («коллектив», «полк» и т. п.) и единичными: «коллектив нашего института», «86-й стрелковый полк», «созвездие Большой Медведицы». В процессе рассуждения общие понятия могут употребляться в разделительном и собирательном смысле. Если высказывание относится к каждому элементу класса, то такое употребление понятия будет разделительным; если же высказывание относится ко всем элементам, взятым в единстве, и неприложимо к каждому элементу в отдельности, то такое употребление понятия является собирательным. Например. высказывая мысль «Студенты нашего института изучают логику», мы употребляем понятие «студенты нашего института» в разделительном смысле, так как данное утверждение относится к каждому студенту института. В высказывании «Студенты нашего института провели теоретическую конференцию» утверждение относится ко всем студентам нашего института в целом. Здесь понятие «студенты нашего института» употребляется в собирательном смысле. Слово «каждый» к данному суждению неприложимо. Понятия делятся на конкретные и абстрактные в зависимости от того, что отражают понятия: предмет (класс предметов) или его свойство (отношение между предметами). Понятие, в котором мыслится предмет или совокупность предметов как нечто самостоятельно существующее, называется конкретным; понятие, в котором мыслится свойство предмета или отношение между предметами, называется абстрактным. Так, понятия «книга», «свидетель», «государство», «происшествие», «обвинение» являются конкретными; понятия «белизна», «смелость», «ответственность» — абстрактными.
Различие между конкретными и абстрактными понятиями основано на различии между предметом, который мыслится как целое, и свойством предмета, отвлеченным от самого предмета и отдельно от предмета не существующим. Абстрактные понятия образуются в результате отвлечения, абстрагирования определенного признака предмета от самого предмета; эти признаки мыслятся как самостоятельные объекты мысли. Так, понятия «смелость», «невменяемость» отражают признаки, не существующие сами по себе, в отрыве от лиц, обладающих этими признаками. Это абстрактные понятия. Не следует смешивать конкретные понятия с единичными, а абстрактные с общими. Общие понятия могут быть и конкретными, и абстрактными (например, понятие «преступление» — общее, конкретное; понятие «преступность» — общее, абстрактное). Как конкретным, так и абстрактным может быть и единичное понятие (например, понятие «Великая Французская революция» — единичное, конкретное; понятие «смелость рядового Смирнова» — единичное, абстрактное). Понятия делятся на положительные и отрицательные в зависимости от того, составляют ли их содержание признаки, присущие предмету, или признаки, отсутствующие у него. Понятия, содержание которых составляют признаки, присущие предмету, называются положительными. Понятия, в содержании которых указывается на отсутствие у предмета определенных признаков, называются отрицательными. Так, понятия «грамотный», «порядок», «логичный», «верующий» являются положительными; понятия «неграмотный», «беспорядок», «алогичный», «неверующий» — отрицательными. В русском языке отрицательные понятия выражаются словами с отрицательными приставками «не» и «без»: «независимость», «небрежность», «беззаконие», «бездействие», «неповиновение», «неисполнение приказа», «недонесение»; в словах иностранного, преимущественно греческого, происхождения — чаще всего словами с отрицательной приставкой «а»: «аморальный», «аполитичный», «асимметрия» и т. д. (Не следует смешивать логическую характеристику понятий как положительных и отрицательных с политической, нравственной, юридической оценкой тех явлений, которые они отражают. Так, понятия «национальная вражда», «преступление» являются положительными: в них указаны признаки, принадлежащие предмету. Однако явления, отраженные в этих понятиях, вызывают у нас отрицательную оценку. Ясно, например, что национальная вражда как объективно существующее явление не может вызвать у человека положительного отношения). Понятия делятся на безотносительные и соотносительные в зависимости от того, мыслятся ли в них предметы, существующие раздельно или в связи с другими предметами. Безотносительные понятия отражают предметы, существующие раздельно и поэтому мыслящиеся вне отношения к другим предметам. Таковы понятия «студент», «государство», «народный суд», «потерпевший», «место преступления» и др. В соотносительных понятиях отражаются предметы, существование которых связано с существованием других предметов, поэтому они не мыслятся один без другого. Например: «родители» и «дети», «начальник» и «подчиненный», «причина» и «следствие». В этих понятиях отражены предметы, существование одного из которых предполагает существование другого.
Определить, к какому виду относится то или иное понятие, значит дать ему логическую характеристику. Так, давая логическую характеристику понятию «юрист», нужно указать, что это понятие общее (нерегистрирующее), конкретное, положительное, безотносительное. Логическая характеристика понятий помогает уточнить их содержание и объем, выработать более точное употребление выражающих их слов. Отношения между понятиями. Отношения между понятиями по объему делятся на две группы; совместимые, когда элементы объема одного понятия частично или полностью принадлежат объему другого понятия, и несовместимые, когда ни один элемент объема одного понятия не принадлежит объему другого понятия. Совместимые понятия могут находиться в отношении равнозначности (тождества), пересечения (перекрещивания), и подчинения (субординации), а несовместимые – в отношении соподчинения (координации), противоположности (контрарности), и противоречия (контрадикторности). Отношение между объемами понятий изображаются с помощью круговых схем. При этом каждый круг обозначает объем какого-либо понятия, а каждая точка круга — элемент этого объема. Для иллюстрации отношения равнозначности (тождества), в котором находятся фактически равные по объему понятия, употребляется схема, показанная на рис. 1. Символы А и В могут обозначать, в частности, А — “прямоугольник с равными сторонами”, В — “квадрат”.
Отношение пересечения, когда объемы понятий совпадают лишь в некоторой своей части (напр., А — “адвокат”, В — “спортсмен”), изображено на рис. 2. Общая часть двух кругов (С) иллюстрирует образованное в результате частичного совпадения объемов двух понятий новое понятие — “адвокат-спортсмен”. Отношение подчинения, когда объем одного понятия полностью входит в объем другого, но не исчерпывает его (напр., В — “город”, А — “населенный пункт”), изображено на рис. 3. При изображении отношений несовместимых понятий возникает необходимость во введении более широкого по объему понятия, которое включало бы объемы несовместимых понятий. Например, для изображения отношения соподчинения, в котором находятся понятия А — “майор” и В — “капитан”, мы должны ввести новое, подчиняющее их понятие С — “офицер” (рис. 4).
Отношение противоположности, в котором находятся два понятия, отражающие крайние моменты в последовательном ряду каких-либо предметов (напр., А — “белый”, В — “черный”), изображено на рис. 5. Схема показывает, что сумма объемов противоположных понятий не исчерпывает объема объединяющего их родового понятия С — “цвет”. Отношение противоречия, в котором находятся положительное и соответствующее ему отрицательное понятие (напр., В — “млекопитающее”, При изображении отношений более чем двух понятий сначала определяются попарно вид отношения, а затем вычерчивается общая схема, отображающая эти отношения. Например, отношения между понятиями А — “рабочий”, В — “член профсоюза”, С — “спортсмен” и D — “рабочий ЗИЛа” можно изобразить схемой, показанной на рис. 8. Операции над классами. Поскольку объем всякого понятия представляет собой некоторое множество предметов, обладающих определенными общими признаками, к ним применим чисто количественный подход. При этом над ними можно производить следующие логические операции: сложение (объединение классов), умножение (пересечение классов) и отрицание класса (образование дополнения к классу). Смысл операции объединения классов состоит в образовании нового класса, включающего все элементы слагаемых классов. Так, например, сложив класс населенных пунктов (А) с классом городов (В), мы получим в сумме класс населенных пунктов (А È В). При пересечении классов образуется новый класс, включающий элементы, общие для умножаемых классов. Например, умножив класс женщин (А) и класс учителей (В), в произведении получим класс учительниц (А Ç В). Сущность образования дополнения к классу состоит в нахождении такого класса, который в сумме с дополняемым классом составляет универсальный класс. Например, дополнением к классу позвоночных животных (А) является класс беспозвоночных животных ( Деление объема понятий. Делением называется логическая операция, раскрывающая объем родового понятия путем перечисления его видов. В делении различают: а) понятие, объем которого подвергается делению, или делимое; б) видовые понятия, получающиеся в результате деления, или члены деления: в) признак, с учетом которого производится деление, или основание деления. Различают: а) деление по видоизменению признака и б) дихотомическое деление. Сущность деления по видоизменению признака состоит в том, что каждый из получаемых в его результате видов приобретает один и тот же признак, лежащий в основании деления, но у каждого из этих видов он находит специфическое проявление. Например, признак “обладать тягой” присущ всем локомотивам, но у паровозов паровая тяга, у электровозов — электрическая, у тепловозов — тепловая. Таким образом, локомотивы можно разделить по характеру тяги на паровозы, электровозы и тепловозы. Сущность дихотомического деления состоит в выделении интересующего нас вида из объема родового понятия и образовании дополнения к этому виду, т.е. понятия, противоречащего данному. Например, животные делятся на позвоночных и беспозвоночных. Производя деление объема понятия по видоизменению признака, необходимо соблюдать следующие правила: 1. Деление должно быть соразмерным, т.е. объем делимого понятия должен быть равен сумме объемов членов деления. При нарушении этого правила возможны ошибки: а) неполное деление, когда некоторые виды при делении опускаются; б) деление с лишними членами, когда среди членов деления называются виды, не соответствующие основанию деления. При достаточно большом количестве членов деления правило соразмерности соблюдается употреблением выражений “и т.д.”, “и т.п.”, “и др.”; 2. Деление должно производиться по одному основанию. Хотя объем одного и того же понятия можно разделить по-разному в зависимости от избранного основания, однако нельзя при однократном делении наряду с видами, соответствующими основанию деления, называть виды, ему не соответствующие. Ошибка, возникающая при нарушении этого правила, называется подменой основания. Например: “Жиры бывают животные, растительные и твердые”. 3. Деление должно быть последовательным, т.е. членами деления должны быть однопорядковые по отношению к делимому понятию виды. Когда наряду с видами первого порядка называются виды иных порядков, возникает ошибка, носящая название “скачок в делении”. Пример: “Грамматические предложения бывают простые, сложные и сложносочиненные”. 4. Члены деления должны исключать друг друга, т.е. находиться в отношении соподчинения, а не пересечения. Деление объема понятий необходимо отличать от членения целого на части. Члены деления представляют собой видовые понятия, обладающие признаками делимого родового понятия, тогда как части не обладают признаками целого. Определение понятий. Определением называется логическая операция, позволяющая раскрывать содержание понятия, отличать предмет, отражаемый понятием, от сходных с ним предметов, устанавливать смысловое значение слова или выражения. В зависимости от того, что определяется (сам предмет или имя, его обозначающее), определения делятся на реальные (определения предметов) и номинальные (определения имен). В определении различают то, что определяется (определяемое понятие, definiendum, сокращенно — Dfd), и то, при помощи чего определяется Dfd (определяющее понятие, definiens, Dfn). Наиболее распространено определение через ближайший род и видовое отличие, сущность которого состоит в том, что при определении какого-либо предмета указывают на ближайшие родовое понятие, в объеме которого мыслится определяемый предмет, и называют его специфический отличительный признак. Общий вид таких определений можно выразить формулой А=Вс, где А — определяемый предмет, В — ближайшее родовое понятие, с — видообразующий признак. Например: “Логика (А) — это наука (В), которая изучает структуру мыслей и законы их построения (с)”. Наиболее часто встречающимися разновидностями родо-видовых определений являются генетеческие, операциональные, целевые и квалифицирующие. Генетическое определение - это определение, в котором видообразующий признак указывается на способ порождения (образования) предметов. Например: Окружность – это замкнутая линия, образованная вращением радиуса определенной длины вокруг неподвижной точки в некоторой плоскости. Операциональное определение – это определение, в котором указывается процедура, посредством которой можно узнать, подпадает произвольный предмет из некоторого класса под данный термин или нет. Например: Кислота – это жидкость, которая окрашивает лакмусовую бумажку в красный цвет. Целевое определение – это определение, в котором указывается на то, как используется предмет, для достижения каких целей он применяется. Например: Транспорт – это средство, с помощью которого осуществляется пространственное перемещение людей и грузов. Квалифицирующим называется определение, с помощью которого фиксируются какие-то структурные особенности предмета, его атрибуты, а также особенности внешнего вида. Например: Квадрат – это прямоугольник с равными сторонами. В науке и обыденном мышлении используются и такие приемы, сходные с определением, как описание, характеристика, указание, дескриптивное определение, различение, пояснение, сравнение и остенсивное определение. Задача описания состоит в том, чтобы более точно и полно перечислить признаки предмета (события, места, где оно произошло, лица и т.д.), причем перечисляются, как правило, внешние признаки. Цель описания — создать наглядный образ предмета, его представление. (Например описание Пугачева в “Капитанской дочке”: “Он был лет сорока, роста среднего, худощав и широкоплеч”.). Характеристика состоит в перечислении внутренних, чувственно не воспринимаемых признаков предмета (характеризуя, например, Пугачева, следовало бы указать, что он донской казак, участник семилетней и русско-турецкой войн, хорунжий, предводитель Крестьянской войны 1773-1775 гг., проявил выдающиеся организаторские способности). Указание — это прием, сходный с определением, с помощью которого выявляется родовое понятие посредством называния его видов. Дескриптивное определение — это прием, сходный с определением, имеющий вид: “Это тот х, который...”. Различение - это прием, сходный с определением, посредством которого показывается отличие каких-либо объектов не от всех других, а лишь от наиболее сходных с ними. Например: Понятие от суждения отличается отсутствием утверждения или отрицания о явлениях действительности. Пояснение – это прием, сходный с определением, суть которого состоит в раскрытии не всего содержания понятия, а лишь части его с какой-либо целью, которая может состоять в том, чтобы подготовить строго логическое определение. Например: Способность к абстрактному мышлению является признаком, отличающим человека от животного. Сравнение – это прием, сходный с определением, применяющийся с целью пояснения одного понятия другим, более ясным, например абстрактное – конкретным. Например: Религия – опиум народа. Остенсивное определение (ostendo лат. – показываю) – это прием, сходный с определением, посредством которого устанавливается значение термина путем демонстрации предмета, обозначаемого этим термином. Это определение применяется для характеристики предметов доступных непосредственному восприятию. Чтобы определение решало свои познавательные задачи, необходимо соблюдать следующие правила: 1. Определение должно быть соразмерным. Это значит, что объем определяемого понятия должен быть равен объему определяющего, т.е. Dfd и Dfn должны быть равнообъемными понятиями. При нарушении этого правила возникают ошибки, которые называются “ слишком широкое определение” (когда Dfn по объему шире Dfd) и “слишком узкое определение” (когда наоборот, Dfd, по объему шире Dfd); 2. В определении не должно содержаться круга. Ошибка “круг в определении” встречается в двух разновидностях: а) “порочный круг”, когда Dfd определяется через Dfn, а в свою очередь Dfn определяется через Dfd; б) тавтология, когда Dfd и Dfn выражены одинаковыми по смыслу терминами; 3. Определение должно быть четким, ясным, не содержащим двусмысленностей. Из этого правила вытекают следующие требования: а) в научных определениях не должно содержаться художественно-образных средств — метафор, сравнений и др.; б) научное определение должно формулироваться в однозначно определенных терминах; в) нельзя определять неизвестное через неизвестное; 4. Определение по возможности не должно быть отрицательным. Тема 3. Суждение. Выделяющие суждения. Суждение, в котором идет речь о признаке, принадлежащем (или не принадлежащем) только предмету мысли и не принадлежащем (принадлежащем) другим предметам, называется выделяющим. Например: “Только студенты исторического факультета изучают археологию”; “Только некоторые параллелограммы — квадраты”. Всякое выделяющее суждение можно разложить на два суждения. При этом в одном из них наличие какого-либо признака у предмета утверждается, а во втором — отрицается. Так, суждение “Только некоторые параллелограммы — квадраты” является синтезом суждений “Некоторые параллелограммы являются квадратами” и “Некоторые параллелограммы не являются квадратами”. Отрицание суждения Отрицанием называется логическое действие, посредством которого образуется новое суждение, истинное тогда и только тогда, когда исходное суждение ложно, и ложное в том случае, если исходное суждение истинно. Термином “отрицание” нередко обозначают суждение, получающееся в результате применения этой операции. Для определения того, какие суждения находятся в отношении отрицания друг к другу, необходимо обратиться к теме “Умозаключения по логическому квадрату” (Тема 5. Умозаключение. Параграф 5. Выводы посредством преобразования суждений). Сложные суждения В теме 1 указывалось, что используя такие семантические категории, как высказывания и заменяющие их переменные, а также функторы (логические союзы) “неверно, что” (`) или (ù),”и” (Ù), “или” (Ú), “либо..., либо” (Ú Смысл логических союзов в логике суждений уточняется с помощью следующих определений: “Неверно, что” (отрицание) (ù) — логический союз, с помощью которого образуется новое суждение, истинное тогда и только тогда, когда исходное суждение (аргумент) ложно, и ложное, когда исходное суждение (аргумент) истинно. “И” (конъюнкция) (Ù) — логический союз, с помощью которого образуется сложное суждение, истинное тогда и только тогда, когда истинным является каждый из аргументов. “Или” (неисключающая дизъюнкция) (Ú) — логический союз, с помощью которого образуется сложное суждение, истинное тогда и только тогда, когда истинным является хотя бы один аргумент. “Либо..., либо” (исключающая дизъюнкция) (Ú) — логический союз, с помощью которого образуется сложное суждение, истинное тогда и только тогда, когда истинным является только один аргумент. “Если..., то” (импликация) (É) — логический союз, с помощью которого образуется сложное суждение, ложное тогда и только тогда, когда первый аргумент (антецедент) истинен, а второй (консеквент) ложен. “Тогда и только тогда, когда” (эквиваленция) («) — логический союз, с помощью которого образуется сложное суждение, истинное тогда и только тогда, когда его аргументы либо истинны, либо ложны. Смысл определенных таким образом логических союзов лишь приблизительно совпадает со смыслом соответствующих грамматических союзов, которые в повседневном обиходе употребляются, как правило, неоднозначно. Определения логических союзов в логике высказываний могут быть заданы также с помощью так называемых таблиц истинности, указывающих на логическое значение сложного суждения, зависящее от логических значений аргументов. Отрицание задается такой таблицей истинности (и — истинно, л — ложно):
Остальные логические союзы имеют следующие таблицы истинности:
Если при одинаковых значениях переменных таблицы истинности двух сложных высказываний совпадают, то такие высказывания называются равносильными. В противном случае они не равносильны и, следовательно, не могут быть взаимозаменяемыми в процессе рассуждения. Тема 4. Законы логики. Закон тождества. Закон тождества формулируется следующим образом: всякая мысль тождественна самой себе. Это значит, что в процессе рассуждения она, сколько бы ни повторялась, должна сохранять одно и то же содержание. Отсюда вытекает, что нельзя нетождественные мысли принимать за тождественные и наоборот. Соблюдение этого требования предохраняет мышление от расплывчатости, туманности, двусмысленности, позволяет достичь определенности, являющейся существенным свойством правильного мышления. Закон тождества выражается так: p есть p (или p= p), p É p. Закон противоречия. Мышление человека должно быть не только ясным, четким и определенным, но и последовательным, непротиворечивым. Последовательность — существенное свойство правильного мышления. Оно выражается в законе противоречия (непротиворечия), который гласит: два противоположных суждения не могут быть одновременно истинными, — по крайней мере, одно из них необходимо ложно. Закон противоречия выражается как: p не есть не-p,ù (p Ùù p). Тема 5. Умозаключение. Дедуктивные умозаключения Среди необходимых умозаключений особое место принадлежит дедуктивным умозаключениям. В основе выделения дедуктивных умозаключений лежит отношение строгого логического следования. Это отношение можно определить следующим образом. Пусть даны два произвольных суждения a и b. В таком случае считается, что из a строго следует b, если и только если всякий раз, когда истинно a, то истинным оказывается и b. Иными словами, истинность b гарантируется с необходимостью истинностью a. Например, суждение ù q É ù p строго следует из суждения p É q. Как видно из таблицы истинности этих выражений, во всех случаях, когда p É q истинно, истинным является и ùq É ùp (см. табл.). (Уместно заметить, что для данных выражений верно и обратное, т.е. из ùq É ùp строго следует p É q).
Из определения строгого логического следования вытекает такое утверждение: из a строго следует b тогда и только тогда, когда a ® b является логическим законом. Его, как и определение можно использовать для установления факта, является ли то или иное ра
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.213.119 (0.02 с.) |

 В
В 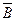 А B
C
Рис.4 Рис. 5 Рис. 6 Рис. 7 Рис. 8
А B
C
Рис.4 Рис. 5 Рис. 6 Рис. 7 Рис. 8
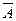 ) и наоборот.
) и наоборот. ), “если..., то” (É), “тогда и только тогда, когда” («), можно создавать новые высказывания и на этой основе строить особого рода рассуждения. Логическая теория, в которой анализируются такого рода высказывания и рассуждения, называется логикой высказываний (логикой суждений).
), “если..., то” (É), “тогда и только тогда, когда” («), можно создавать новые высказывания и на этой основе строить особого рода рассуждения. Логическая теория, в которой анализируются такого рода высказывания и рассуждения, называется логикой высказываний (логикой суждений).


