
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложные суждения. Таблицы истинности сложных суждений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Состав сложного суждения Сложные суждения состоят из ряда простых («Человек не стремится к тому, во что не верит, и любой энтузиазм, не подкрепляясь реальными достижениями, постепенно угасает»), каждое из которых в математической логике обозначается латинскими буквами (A, B, C, D… a, b, c, d…). В зависимости от способа образования различают конъюнктивные, дизъюнктивные, импликационные, эквивалентные и отрицательные суждения. Дизъюнктивные суждения образуются с помощью разделительных (дизъюнктивных) логических связок (аналогичных союзу «или»). Подобно простым разделительным суждениям, они бывают: § нестрогими (нестрогая дизъюнкция), члены которой допускают совместное сосуществование («то ли…, то ли…»). Записывается как § строгими (строгая дизъюнкция), члены которой исключают друг друга (либо одно, либо другое). Записывается как Импликационные суждения образуются с помощью импликации, (эквивалентно союзу «если …, то»). Записывается как Конъюнктивные суждения образуются с помощью логических связок сочетания или конъюнкции (эквивалентно запятой или союзам «и», «а», «но», «да», «хотя», «который», «зато» и другим). Записывается как Эквивалентные суждения указывают на тождественность частей суждения друг другу (проводят между ними знак равенства). Помимо определений, поясняющих какой-либо термин, могут быть представлены суждениями, соединенными союзами «если только», «необходимо», «достаточно» (например: «Чтобы число делилось на 3, достаточно, чтобы сумма цифр, его составляющих, делилась на 3»). Записывается как Отрицательные суждения строятся с помощью связок отрицания «не». Записываются либо как a ~ b, либо как a b (при внутреннем отрицании типа «машина не роскошь»), а также с помощью черты над всем суждением при внешнем отрицании (опровержении): «не верно, что …» (a b). Таблица истинности – таблица, с помощью которой устанавливается значение истинности сложного суждения в зависимости от значения истинности простых суждений, входящих в его состав. Каждое из сложных суждений имеет свою таблицу истинности. В классической логике сводные данные для конъюнкции, дизъюнкции, импликации и эквиваленции имеют следующий вид Таблица истинности – это таблица, устанавливающая соответствие между всеми возможными наборами логических переменных, входящих в логическую функцию, и значениями функции.
Таблицы истинности находят широкое применение для · Вычисления истинности сложных высказываний; · Установления эквивалентности высказываний; · Определения тавтологий.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 2862; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.219.203 (0.006 с.) |

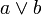 ;
; .
. или
или  . В естественном языке союз «если …, то» иногда является синонимом союза «а» («Погода изменилась и, если вчера было пасмурно, то сегодня не одной тучи») и, в таком случае, означает конъюнкцию.
. В естественном языке союз «если …, то» иногда является синонимом союза «а» («Погода изменилась и, если вчера было пасмурно, то сегодня не одной тучи») и, в таком случае, означает конъюнкцию. .
. (у разных математиков по-разному, хотя математический знак тождества всё-таки
(у разных математиков по-разному, хотя математический знак тождества всё-таки  ).
).


