
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дихотомическое деление. Классификация, ее значение.Содержание книги
Поиск на нашем сайте
Суждение и его сущность. Виды суждений. Простое категорическое суждение. Суждение — форма мышления, в которой что-либо утверждается или отрицается о предмете, его свойствах или отношениях между предметами. Виды суждений и отношения между ними изучаются в философской логике. В формальной и математической логике суждениям соответствуют высказывания. Виды суждения: Простые и сложные суждения Простые суждения — суждения, составными частями которых являются понятия. Простое суждение можно разложить только на понятия. Сложные суждения — суждения, составными частями которых являются простые суждения или их сочетания. Сложное суждение может рассматриваться как образование из нескольких исходных суждений, соединенных в рамках данного сложного суждения логическими союзами (связками). От того, при помощи какого союза связываются простые суждения, зависит логическая особенность сложного суждения. Простое категоричное суждения. Состав простого суждения Простое (атрибутивное) суждение — это суждение о принадлежности предметам свойств (атрибутов), а также суждения об отсутствии у предметов каких-либо свойств. В атрибутивном суждении могут быть выделены термины суждения — субъект, предикат, связка, квантор. § Субъект суждения — это мысль о каком-то предмете, понятие о предмете суждения (логическое подлежащее). § Предикат суждения — мысль об известной части содержания предмета, которое рассматривается в суждении (логическое сказуемое). § Логическая связка — мысль об отношении между предметом и выделенной частью его содержания (иногда только подразумевается). § Квантор — указывает, относится ли суждение ко всему объёму понятия, выражающего субъект, или только к его части: «некоторые», «все» и т. п. Опираясь на уже известное определение простого суждения, категорическое суждение (суждение действительности) можно определить как такое, в котором что-то утверждается или отрицается относительно предмета мысли. Другими словами — это такое простое суждение, в котором между субъектом и предикатом устанавливается категорическая (утвердительная или отрицательная) связь, т.е. отношение тождества, подчинения, частичного совпадения, противоречия, противоположности и соподчинения: "Жучка есть собака», «Студент не есть профессор» и т.п. Как и любое суждение, простое категорическое суждение может быть истинным («и») или ложным («л»). В языке это суждение выражается повествовательным предложением, при этом тесная связь и взаимозависимость суждения и предложения не является основанием для их отождествления. Структура простого категорического суждения обычно представляется трехэлементной, т.е. такое суждение состоит из субъекта, предиката и связки, что удобно представить в виде формулы: S--P. Но здесь непроизвольно опускается тот элемент, который связан с количественной характеристикой субъекта суждения, т.е. квантор. C учетом его приходится говорить о четырех элементах простого категорического суждения. Символическое изображение такого суждения уже приводилось. Логическая связь (утверждение или отрицание), т.е. связка между субъектом и предикатом простого категорического суждения выступает основным структурным законом, необходимой связью элементов, формирующих целостность данной форму мысли. Простые категорические суждения по количественному и качественному признакам подразделяются на виды. По количественному (объемному) показателю, выражаемому квантором, простые категорические суждения делятся на единичные, частные и общие. Единичное суждение отражает единственный предмет мысли, т.е. субъект этого суждения — единичное понятие: «Крупнейший город Северо-Запада нашей страны расположен в устье Невы». Частное суждение отражает некоторую совокупность предметов, но не всю, что и подчеркивается квантором: «Некоторые S есть Р», «Многие студенты — отличники», «Встречаются такие S, которые есть Р».
Классификация суждений. По качеству § Утвердительные — S есть P. Пример: «Люди пристрастны к самим себе». § Отрицательные — S не есть P. Пример: «Люди не поддаются лести». [править]По объёму § Общие — суждения, которые справедливы относительно всего объёма понятия (Все S суть P). Пример: «Все растения живут». § Частные — суждения, которые справедливы относительно части объема понятия (Некоторые S суть P). Пример: «Некоторые растения суть хвойные». [править]По отношению § Категорические — суждения, в которых сказуемое утверждается относительно субъекта без ограничений во времени, в пространстве или обстоятельствах; безусловное суждение (S есть P). Пример: «Все люди смертны». § Условные — суждения, в которых сказуемое ограничивает отношение каким-либо условием (Если А есть В, то С есть D). Пример: «Если дождь пойдет, то почва будет мокрая». Для условных суждений § Основание — это (предыдущее) суждение, которое содержит условие. § Следствие — это (последующее) суждение, которое содержит следствие. [править]По отношению между подлежащим и сказуемым
Логический квадрат, описывающий отношения между категорическими суждениями Субъект и предикат суждения могут быть распределены (индекс «+») или не распределены (индекс «-»). § Распределено — когда в суждении подлежащее (S) или сказуемое (P) берется в полном объеме. § Не распределено — когда в суждении подлежащее (S) или сказуемое (P) берется не в полном объёме. Суждения А (обще-утвердительные суждения) Распределяет свое подлежащее (S), но не распределяет свое сказуемое (P) Объем подлежащего (S) меньше объема сказуемого (Р) § Прим.: «Все рыбы суть позвоночные» Объемы подлежащего и сказуемого совпадают § Прим.: «Все квадраты суть параллелограммы с равными сторонами и равными углами»
В этом суждении мы отрицаем всякое совпадение между подлежащим и сказуемым § Прим.: «Ни одно насекомое не есть позвоночное»
Часть класса подлежащего входит в класс сказуемого. § Прим.: «Некоторые книги полезны» § Прим.: «Некоторые животные суть Позвоночные»
§ Прим.: «Некоторые животные не суть позвоночные (S)» § Прим.: «Некоторые змеи не имеют ядовитых зубов (S)»
таблица распределения подлежащего и сказуемого
Общая классификация: § общеутвердительные (A) — одновременно общие и утвердительные («Все S+ суть P-») § частноутвердительное (I) — частное и утвердительное («Некоторые S- суть P-») Прим: «Некоторые люди имеют черный цвет кожи» § общеотрицательное (E) — общее и отрицательные («Ни один S+ не суть P+») Прим: «Ни один человек не всеведущ» § частноотрицательное (O) — частное и отрицательное («Некоторые S- не суть P+») Прим: «Некоторые люди не имеют черного цвета кожи» [править]Другие § Разделительные - 1) S есть или А, или В, или С 2) или А, или В, или С есть Р когда в суждении остается место неопределенности § Условно-разделительные суждения - Если А есть В, то С есть D или Е есть F если есть А, то есть а, или b, или с Прим: «Если кто желает получить высшее образование, то он должен учиться или в университете, или в институте, или в академии»
§ Суждения тождества — понятия субъекта и предиката имеют один и тот же объём. Пример: «Всякий равносторонний треугольник есть равноугольный треугольник». § Суждения подчинения — понятие с менее широким объёмом подчиняется понятию с более широким объёмом. Пример: «Собака есть домашнее животное». § Суждения отношения — именно пространства, времени, отношения. Пример: «Дом находится на улице».
§ Экзистенциальные суждения или суждения существования — это такие суждения, которые приписывают только лишь существование. § Аналитические суждения — суждения, в которых мы относительно субъекта высказываем нечто такое, что в нём уже содержится. § Синтетические суждения — суждения, расширяющие познание. В них не раскрывается содержание подлежащего, а присоединяется нечто новое. [править]Модальность суждений Основная статья: Модальная логика Модальные понятия, или модальности — понятия, выражающие контекстную рамку суждения: время суждения, место суждения, знание о суждении, отношение говорящего к суждению. В зависимости от модальности выделяются следующие основные виды суждений: § Суждения возможности — «S, вероятно, есть Р» (возможность). Пример: «Возможно падение метеорита на Землю». § Ассерторические — «S есть P» (действительность). Пример: «Киев стоит на Днепре». § Аподиктические — «S необходимо должно быть P» (необходимость). Пример: «Две прямые линии не могут замыкать пространства».
Состав сложного суждения Сложные суждения состоят из ряда простых («Человек не стремится к тому, во что не верит, и любой энтузиазм, не подкрепляясь реальными достижениями, постепенно угасает»), каждое из которых в математической логике обозначается латинскими буквами (A, B, C, D… a, b, c, d…). В зависимости от способа образования различают конъюнктивные, дизъюнктивные, импликационные, эквивалентные и отрицательные суждения. Дизъюнктивные суждения образуются с помощью разделительных (дизъюнктивных) логических связок (аналогичных союзу «или»). Подобно простым разделительным суждениям, они бывают: § нестрогими (нестрогая дизъюнкция), члены которой допускают совместное сосуществование («то ли…, то ли…»). Записывается как § строгими (строгая дизъюнкция), члены которой исключают друг друга (либо одно, либо другое). Записывается как Импликационные суждения образуются с помощью импликации, (эквивалентно союзу «если …, то»). Записывается как Конъюнктивные суждения образуются с помощью логических связок сочетания или конъюнкции (эквивалентно запятой или союзам «и», «а», «но», «да», «хотя», «который», «зато» и другим). Записывается как Эквивалентные суждения указывают на тождественность частей суждения друг другу (проводят между ними знак равенства). Помимо определений, поясняющих какой-либо термин, могут быть представлены суждениями, соединенными союзами «если только», «необходимо», «достаточно» (например: «Чтобы число делилось на 3, достаточно, чтобы сумма цифр, его составляющих, делилась на 3»). Записывается как Отрицательные суждения строятся с помощью связок отрицания «не». Записываются либо как a ~ b, либо как a b (при внутреннем отрицании типа «машина не роскошь»), а также с помощью черты над всем суждением при внешнем отрицании (опровержении): «не верно, что …» (a b). Таблица истинности – таблица, с помощью которой устанавливается значение истинности сложного суждения в зависимости от значения истинности простых суждений, входящих в его состав. Каждое из сложных суждений имеет свою таблицу истинности. В классической логике сводные данные для конъюнкции, дизъюнкции, импликации и эквиваленции имеют следующий вид Таблица истинности – это таблица, устанавливающая соответствие между всеми возможными наборами логических переменных, входящих в логическую функцию, и значениями функции.
Таблицы истинности находят широкое применение для · Вычисления истинности сложных высказываний; · Установления эквивалентности высказываний; · Определения тавтологий. Правила фигур силлогизма Как видно из анализа модусов 1-й фигуры, они имеют следующие два правила: 1. Бόльшая посылка – общее суждение 2. Меньшая посылка – утвердительное суждение. Модусы 2-й фигуры указывают на следующие правила: 3. Бόльшая посылка – общее суждение 4. Одна из посылок – отрицательное суждение. 3-я фигура имеет такие правила: 5. Меньшая посылка – утвердительное суждение 6. Заключение – частное суждение. 4-я фигура также имеет свои правила и модусы. Однако выведение заключения из посылок по этой фигуре не характерно для естественного процесса рассуждения.
23.Условно-категорическое умозаключение. Ошибки в условно-категорических умозаключениях. Условно-категорическим называется умозаключение, одна из посылок которого является условным суждением, а другая посылка и вывод — категорическими суждениями. Условное суждение имеет форму: если A есть B, то C есть D, например: если Земля вращается вокруг своей оси, то происходит смена дня и ночи. Первое суждение есть основание (антецедент), а второе — следствие (консеквент). Существуют два модуса условно-категорических умозаключений. Первый из них называется modus ponens, то есть устанавливающий, утверждающий, конструктивный модус; второй называется modus tolens, то есть разрушающий, отрицающий, деструктивный модус. Конструктивный модус имеет следующий вид. Если A есть B, то C есть D; A есть B; Следовательно, C есть D. Например: Если Земля вращается вокруг Солнца, то происходит смена дня и ночи; Земля вращается вокруг Солнца; Следовательно, происходит смена дня и ночи.
Это правило связано с тем, что при несовместимых суждениях-антецедентах, одно из которых ложно, возможно истинное заключение: если Земля вращается вокруг Солнца, то происходит смена дня и ночи, если Солнце вращается вокруг Земли, то происходит смена дня и ночи, поэтому нельзя сделать заключение: *происходит смена дня и ночи, следовательно, Земля вращается вокруг Солнца. Деструктивный модус имеет следующий вид. Если A есть B, то C есть D; C не есть D; Следовательно, A не есть B.
При отрицании следствия любой из возможных в принципе альтернативных антецедентов окажется ложным: если смены дня и ночи не происходит, то Земля не вращается вокруг Солнца и Солнце не вращается вокруг Земли. Если человек есть мера всех вещей, то принципы нравственности условны; Принципы нравственности не условны; Следовательно, человек не есть мера всех вещей. Рассмотрим, однако, следующие умозаключения, которые иногда подводят преподавателя: Если студент слушает лекции, то он приобретает необходимые познания; Студент N слушал лекции; Следовательно, он приобрел необходимые познания. Или: Если студент слушает лекции, то он приобретает необходимые познания; Студент N не приобрел необходимых познаний; Следовательно, он не слушал лекции. Понятно, что оба они могут оказаться ложными, ибо не всякий, кто слушает лекции, понимает их.
Итак, доказательным (при условии истинности большей посылки) будет следующее рассуждение: Если и только если студент слушает лекции, он приобретает необходимые познания; Студент N не приобрел необходимых познаний; Следовательно, он не слушал лекций.
Дихотомическое деление. Классификация, ее значение. Дихотоми́я (греч. διχοτομία: δῐχῆ, «надвое» + τομή, «деление») — раздвоенность, последовательное деление на две части, не связанные между собой. Дихотомическое деление в математике, философии, логике и лингвистике является способом образования взаимоисключающих подразделов одного понятия или термина и служит для образования классификации элементов. Дихотомическое деление не всегда заканчивается установлением двух противоречащих понятий. Иногда отрицательное понятие вновь делится на два понятия, что помогает выделить из большого круга предметов группу предметов, интересующих нас в каком-либо отношении. Пример Объём понятия «человек» можно разделить на два взаимоисключающих класса: мужчины и не мужчины. Понятия «мужчины» и «не мужчины» являются противоречащими друг другу, поэтому их объёмы не пересекаются. От дихотомии следует отличать обычное деление, приводящее к тому же самому результату. Например, объём понятия «человек» можно разделить по признаку пола на мужчин и женщин. Но между понятиями мужчина и женщина нет логического противоречия, поэтому здесь нельзя говорить о дихотомическом делении. Классификация - это сложный вид деления с основанием, состоящим из нескольких признаков, включающий несколько уровней. В классификации каждый член деления получает строго определенное, единственное место в получившейся системе. Основные разновидности классификаций: 1. Естественными классификациями называют классификации, в которых в качестве основания берутся признаки самих классифицируемых предметов. 2. Вспомогательные (технические) классификации - это классификации, в которых в качестве основания деления берутся признаки, которые человек сам привносит в предметы с учетом собственного удобства, например, легкой и оперативной доступности (всякого рода системы маркировки, составление каталогов по алфавиту и т.п.). Среди естественных различают классификации на основе существенных признаков, их-то и считают в полном смысле научными классификациями, и классификации на основе произвольных признаков, т.е. такие, относительно оснований которых неясно являются ли соответствующие признаки существенными или нет. Такие классификации были названы в свое время искусственными, хотя это слово следовало бы закрепить за вспомогательными или техническими классификациями. Как в отношении всякого деления, так и в отношении любой классификации следует соблюдать некоторые основные правила деления, избегать определенных ошибок. Различают следующие основные правила деления и связанные с ними ошибки: а) в каждом делении должно быть строго определенное, единственное основание, которое не изменяется на протяжении всего деления (правило основания). Ошибка, которая при этом совершается, называется "подменой, или потерей основания". Так, нельзя делить понятие "республика" на "парламентские", "президентские" и "федеративные", поскольку здесь явно смешиваются два различных основания; б) деление должно быть соразмерным (правило соразмерности), то есть совокупность объемов членов деления должна полностью исчерпывать объем делимого понятия. При делении не должен быть пропущен ни один предмет из объема делимого понятия и не должен появиться ни один лишний предмет. Соответственно ошибки, которые здесь могут встретиться, называются "слишком узкое деление" (когда при перечислении членов деления некоторые из них теряются, не указываются, упускаются) и "слишком широкое деление" (когда появляются лишние, не входящие в объем делимого понятия части). в) члены деления должны взаимно исключать друг друга, быть в состоянии несовместимости (соподчинения, или субординации, противоположности, противоречия). Ошибка, которая при этом нередко допускается, называется "смешением членов деления". Она встречается в том случае, когда какой-нибудь элемент объема делимого понятия входит одновременно в объемы двух и более членов деления; г) деление должно быть непрерывным (правило многоступенчатого деления). Все члены деления должны являться ближайшими вида-ми исходного понятия, выделяемыми по выбранному основанию. Ошибка, которая при этом может быть совершена, называется "скачок в делении". Она встречается в том случае, если члены деления не являются ближайшими видами делимого понятия, т.е. можно найти такие понятия среди членов деления, которые будут выступать видами для делимого понятия и родами для других членов деления. Для классификационного деления большое значение имеет последнее правило - правило непрерывности, поскольку классификация, как правило, включает в себя несколько (много) уровней деления, (достаточно вспомнить классификации животных и растений в биологии).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 800; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.157.241 (0.009 с.) |


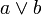 ;
; .
. или
или  . В естественном языке союз «если …, то» иногда является синонимом союза «а» («Погода изменилась и, если вчера было пасмурно, то сегодня не одной тучи») и, в таком случае, означает конъюнкцию.
. В естественном языке союз «если …, то» иногда является синонимом союза «а» («Погода изменилась и, если вчера было пасмурно, то сегодня не одной тучи») и, в таком случае, означает конъюнкцию. .
. (у разных математиков по-разному, хотя математический знак тождества всё-таки
(у разных математиков по-разному, хотя математический знак тождества всё-таки  ).
).


