
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие методические указания по выполнению лабораторных работСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение полных сопротивлений и измерение длины волны в волноводе Цель работы
Приборы и принадлежности 1. Генератор дециметрового диапазона ГЗ-10А. 2. Измерительная коаксиальная линия. 3. Милливольтметр. 4. Согласованная нагрузка. 5. Развязывающий аттенюатор. 6. Короткозамыкающая заглушка. 7. Исследуемые нагрузки. Краткая теория метода Основные понятия о характеристиках процессов в линии передачи В зависимости от возмущения электромагнитной волны в волноводе подразделяются на волны типа Е=ТМ – плоские магнитные волны, в которых отсутствует продольная составляющая магнитного поля Н, и волны типа Н=ТЕ – при отсутствии продольной составляющей электрического поля Е. В коаксиальных измерительных линиях чаще всего используется плоская волна типа ТЕМ, не имеющая продольных компонентов Е и Н. Электрические силовые линии направлены радиально от центрального проводника к внешнему, а магнитные – концентрическими окружностями вокруг центрального провода. Возьмем измерительную линию, слева присоединенную к генератору СВЧ а справа к измеряемой нагрузке (рис. 1). направим ось х от генератора к нагрузке вдоль измерительной линии с началом отсчета в некоторой точке х =0.
рис. 1 При включении генератора в волноводе измерительной линии установятся стоячие волны, так как часть энергии поля будет отражаться от нагрузки. Поперечные составляющие полей Е и Н могут быть представлены как сумма падающей и отраженной волн (т.е. идущей в положительном направлении Е+ и в отрицательном Е- соответственно): Е=Е++Е-, (3) Н=Н++Н-. (3’) Коэффициентом отражения ρ в данной точку волновода называется комплексная величина, равная отношению взятых в этой точке поперечных составляющих Е и Н:
При этом Коэффициент отражения зависит от точки, в которой он определяется, так как при перемещении по волноводу фазы волн изменяются. в самом деле, для начала отсчета (точки 0):
а любой другой точки для волновода без потерь:
но поэтому
и мы получим:
Здесь Характеристическим или волновым сопротивлением волновода Z0 называется отношение поперечных компонент полей Е и Н для бегущей волны:
Оно является неизменным для любой точки. Полным сопротивлением волновода в данной точке называют комплексную величину, равную отношению полей (3) и (3*):
или учитывая (4), (4*) и (7),
Таким образом, для определения полного сопротивления в данной точке волновода необходимо измерить в ней коэффициент отражения ρ. Для измерения модуля ρ достаточно измерить коэффициент бегущей волны S (КБВ) или обратную ему величину – коэффициент стоячей волны (КСВ). Коэффициентом стоячей волны называют отношение напряженностей полей в точках минимума (Еmin) и максимума (Emax) электрического поля (рис.1)
Процесс образования в волноводе стоячих волн для некоторой точки удобно представить графически:
Рис. 2 Из рис. 2 видно, что картина стоячих волн получится в согласии с рис. 1, если вектор Е- вращать против часовой стрелки. Из этих же рисунков ясно, что
Если из эксперимента известны Еmin и Emax, то используя (10), можно определить модуль коэффициента отражения:
Для определения фазы коэффициента отражения достаточно измерить расстояние данной точки от ближайшего минимума, где фаза принимается равной (2n-1)π. Тогда для точки минимума по (6): φ=φ0+2βxmin=(2n-1) π, откуда: φ0=(2n-1)π -2βxmin, и для точки х, в которых нужно определить фазу, будем иметь φ=(2n-1) π -2βxmin+2βx=(2n-1) π -2β(х-хmin), (12) Принимаем условие, при котором φ всегда расположено в интервале между - π и + π, тогда n=0. Обозначая х-хmin=dmin, окончательно получим: φ=-2βdmin- π, (13) На практике определяют обычно местоположение минимума и измеряют расстояние до него со стороны нагрузки, а не со стороны источника. Расчетная часть
По данным значениям модуля
Порядок выполнения работы
1. Изучить теорию метода, описание измерительной линии PI-18, генератора ГЗ-10А. 2. Подготовить установку для измерений, для этого: 2.1. Собрать установку согласно её блок-схеме. Выход измерительной линии подключить к короткозамыкающей заглушке. Аттенюатор выхода мощности генератора поставить на минимум. Каретку измерительной линии установить около середины. Частоту генератора установить около середины диапазона. 2.2. Включить генератор и дать ему прогреться в течении 5 минут на непрерывной генерации. 2.3. Поставить индикатор подстройки резонатора каретки PI-18 в соответствии с частотой генератора. 2.4. Выводя аттенюатор, увеличить выходную мощность генератора, не превышая допустимой мощности до появлений показаний индикатора измерительной линии. Если при увеличении выходной мощности генератора индикатор не даёт показаний, значит, либо зонд каретки PI-18 находится вблизи минимума стоячей волны (тогда его следует сместить вправо или влево на несколько сантиметров), либо не настроен объемный резонатор каретки (нужно вращать микрометрический винт подстройки резонатора), либо неисправен детектор индикатора каретки. Получив показания индикатора, сместить каретку до максимальных показаний индикатора (пучность стоячей волны), подстроить объемный резонатор каретки до максимальных показаний индикатора (изменяя также выходную мощность), а за тем для уменьшения связи индикатора каретки с линией расстроить резонатор до половины показаний индикатора. После этого, увеличивая мощность на выходе генератора (пучность стоячей волны), довести показания индикатора до 85-90 делений. После этих операций установка к работе готова. 4. Получить картинку стоячих волн и измерить длину волны λg в волноводе измерительной линии: 1. Сместить каретку PI-18 в крайнее левое положение, и перемещая ее до конца в право, пронаблюдать картину распределения стоячих волн в измерительной линии. При правильной подготовке установки к измерению индикатор PI-2 в узлах стоячей волны должен показать нуль, а в пучностях не выходить за пределы максимальных показаний. Проделать указанную операцию, отмечая по оси абсцисс на миллиметровой бумаге перемещение каретки, а по оси ординат - показания индикатора. В пределах одной полуволны делать 10-15 отсчетов, при этом поскольку минимумы значительно острее максимумов, отсчеты проводить вблизи них значительно чаще. Указанное проделать в обе стороны движения каретки. Подсчитать по полученным измерениям длину волны по расстояниям между точками минимумов, используя при этом метод «вилки». Из полученных 8-10 отсчетов длины волны найти среднее значение и погрешность измерения. 5. Измерить комплексные сопротивления некоторых нагрузок генератора. 2. Определение начала отсчёта измерительной линии: В длинноволновой радиотехнике за начало отсчета длин в линиях передачи часто принимают либо местоположение (координату) генератора, либо нагрузки. Поскольку на сверхвысоких частотах нагрузки часто соизмеримы с длинной волны, нет необходимости говорить о «координате нахождения нагрузки». Тоже относится и к генератору. Поэтому на СВЧ, как правило, за начало отсчета принимают один из минимумов стоячей волны при коротком замыкании измерительной линии.
Если частота генератора не низменна, то, воспользовавшись данными пункта 3, за начало отсчёта принимают координату минимума, ближайшего к правому концу линии (точка Р на рис. 8).
рис. 8 3. измерение комплексных сопротивлений нагрузки:
Для измерения Z некоторой нагрузки необходимо согласно формуле (8) найти коэффициент отражения Кривая 1 представляет собой эпюру стоячих волн при коротком замыкании линии (как на рис. 8), кривая 2 – при присоединении исследуемой нагрузке. Из рис. 9 видно, что, во-первых, минимум стоячей волны сместиться в точку Р на величину ∆L и, во-вторых, появился отличный от нуля коэффициент бегущей волны:
Из полученной эпюры определяется
φ=-2βdmin- π, (12*) где
Полученное значение
Рис. 9
Задания по пункту 4
8. Измерить генератор комплексного сопротивления фиксированного аттенюатора по частоте генератора, используемой в пункте 3. 9. Измерить комплексные сопротивления коаксиальных волноводов. 10. При обработке результатов измерений необходимо произвести градуировку кристаллического детектора линии. Для этого можно воспользоваться результатами измерений пункта 3. В линии должно быть синусоидальное пространственное распределение поля, когда волновод замкнут короткозамыкающей пластиной. На зависимости 11. Отклонение экспериментальной кривой от теоретической учитывается при подсчёте погрешностей измерений комплексного сопротивления. Градуировку детектора и выбор начала отсчёта следует проводить всякий раз при изменении частоты генератора. В ряде случаев измеряемый КБВ (S) – величина малая, поэтому его определение по отношению Emin/Emax неточно. для более точного определения необходимо (рис. 10):
4. поместить каретку с зонтом в минимум стоячей волны; 5. Увеличить мощность генератора (в пределах допустимой), довести показания индикатора зонда до 1015 делений. Перемещая каретку поставить точно в минимум стоячей волны. Записать это положение каретки (x0) и показания индикатора; 6. сместить каретку влево от x0 до удвоенных показаний индикатора. Записать это положение каретки (x1) и показания индикатора.
Рис. 10 6. Проделать ту же операцию, смещая каретку от х0 вправо. Зафиксировать это положение (x2). Из полученных данных определить коэффициент бегущей волны, который при квадратичной характеристике детектора находится по формуле:
При обработке результатов измерений определение импедансов проводится как расчетным путем (по форм. 18), так и по номограмме расчетных сопротивлений. Полученные результаты сравниваются.
Отчёт должен содержать следующие материалы: 12. Расчётные данные по определению полных сопротивлений. 13. Блок-схему лабораторной установки. 14. Экспериментальные данные по измерению длинны волны. 15. Эпюры стоячих волн при короткозамкнутой и нагруженной линии. 16. Эпюру градуировок детектора. 17. Экспериментальные данные по измерению полных сопротивлений нагрузок. 18. Сравнение величин сопротивлений, полученных расчетным путем и при использовании круговой номограммы полных сопротивлений.
Контрольные вопросы 19. Как определяется полное сопротивление на сверхвысоких частотах? Какие существуют методы измерения сопротивлений? 20. Как определяется полное сопротивление методом измерительной линии? 21. Что называется коэффициентом отражения, КСВ (КБВ)? связь между ними. Как определяется модель и фаза коэффициента отражения? 22. Выражение для полного сопротивления нагрузки. Преобразование полного сопротивления? 23. Объясните принцип построения диаграммы Вольперта. Какие основные применения диаграммы Вольперта? 24. Устройство и принцип действия измерительной линии? 25. Как осуществляется градуировка детектора измерительной линии? 26. Как измерить длину волны, КСВ и входное сопротивление с помощью измерительной линии? 27. Источники ошибок при работе с измерительной линией.
Литература
28. Лебедев Н.В. Техника и приборы СВЧ. – М.: Высшая школа, 1970.-Т.1. 29. Мирский Г.А. Радиоэлектронные измерения. –М.: Энергия, 1976. 30. Валитов Р.А., Сретенский В.Н. Радиотехнические измерения. –М.: Советское радио, 1970. 31. Стариков В.Д. Методы измерений на СВЧ с применением измерительных линий. –М.: Советское радио, 1972. 32. Дворяшин Б.В., Кузнецов Л.И. Радиотехнические измерения. –М.: Советское радио, 1978. 33. описание измерительной линии PI-2. 34. Описание генератора ГЗ-10А.
Сведения из теории Прямоугольный волновод, представляющий металлическую пустотелую трубу прямоугольного сечения, предназначенный для передачи электромагнитной энергии в диапазоне сантиметровых и миллиметровых длин волн, показан на рис.1 вместе с используемой системой координат. При решении задач распространения электромагнитных волн в волноводе сначала находят собственные волны, распространяющиеся по однородному прямолинейному волноводу бесконечной длинны, которые являются решениями однородного уравнения Гельмгольца для комплексных амплитуд векторов поля в волноводе.
Электромагнитные волны могут переносить энергию лишь вдоль волновода, поэтому усредненный за период колебаний вектор Пойнтинга может иметь только одну составляющую
и его величина полностью определяется поперечными составляющими напряженностей электрического и магнитного полей, существующих в волноводе. Поэтому, для решения задач передачи энергии достаточно найти лишь поперечные составляющие поля. Поперечные составляющие напряженностей полей в волноводе для собственных волн могут быть легко определены, если найдено решение однородного уравнения Гельмгольца для векторных потенциалов поля, ориентированных по оси Z. Но для пустотелых волноводов решение часто ищут иначе. Как показано в (1) собственные волны таких волноводов можно разделить на два типа: волны типа «Е», которые имеют продольную составляющую напряженности электрического поля в волноводе Еz (причем Hz=0), и волны типа «Н», имеющие продольную составляющую напряженности магнитного поля в волноводе Hz (причем Ez=0). В этом случае поперечные составляющие напряженностей поля в волноводе могут быть выражены непосредственно через продольные составляющие полей.
Рис. 1. Прямоугольный металлический трубчатый волновод
Рис.2 Диаграмма существования волн различных типов в прямоугольном волноводе.
Методика определения полей в прямоугольном волноводе обычно сводится к следующему: а) предполагается, что стенки волновода идеально проводящие и форма поверхностей стенок идеальна; б) записывается однородное уравнение Гельмгольца для составляющей Нz и ищется его решение в виде распространяющейся вдоль оси Z волны методом разделения переменных; в) пользуясь уравнениями Максвелла, определяют поперечные составляющие напряженностей электрического и магнитного полей в волноводе, выражая их через Нz; г) пользуясь принципом перестановочной двойственности уравнений электродинамики, находят общее решение для волн типа «Е»; д) на найденные в пп. б), в), г) решения накладывают граничное условие Еt=0 на стенках волновода, определяют постоянные интегрирования и получают решения в окончательном виде. При заданных поперечных размерах волновода и длине волн генератора (длине волны колебания, создаваемого генератором, измеряемой в свободном пространстве) l0, волны типов «Е» и «Н» характеризуются двумя числовыми индексами m, n. Колебания с заданными индексами могут существовать лишь в определенных диапазонах длин волн, как это показано на диаграмме существования волн в прямоугольном волноводе, приведенной на рис.2. Как видно из рис.2, в некотором диапазоне длин волн в волноводе может распространяться лишь одна волна, она называется волной основного типа. В прямоугольном волноводе волной основного типа является Н10, которая имеет три составляющие поля (2):
где
На рис.3 показана картина силовых линий напряженностей поля в волноводе, построенная по (2), а на рис.4 приведены графики, показывающие изменения амплитуд составляющих волны в поперечном направлении и изменение мгновенных значений составляющих поле в продольном направлении. При произвольной системе сторонних источников, возбуждающих волновод, или в неоднородном волноводе поле может быть представлено в виде разложения по собственным волнам волновода (в виде суперпозиции собственных волн, имеющих разные амплитуды). Но в большинстве технических устройств размеры волновода выбираются таким образом, что в нем может распространяться только волна основного типа.
Рис.3. Картина силовых линий для волны Н10
Рис.4. Распределение амплитуд составляющих поля в поперечном сечении волновода и зависимость мгновенных значений от координаты Z для момента времени t=0.
Диапазон длин волн, в котором существует только волна основного типа, с нижней стороны ограничен значениями длин волн, при которых по волноводу могут распространятся высшие типы волн, а с верхней стороны ограничен значением lкр=2а. Колебания, у которых l0 >=lкр, не могут распространяться по волноводу в виде бегущей волны, так как для них постоянная b становится мнимой, как видно из (2). Амплитуда таких колебаний экспоненциально уменьшается при увеличении Z. Длина волны l0=lкр называется длинной критической волны основного типа в волноводе или длинной критической волны для волновода - это наибольшая длинна волны, до которой поле основного типа в волноводе может существовать в виде бегущей (распространяющейся) волны. Колебания в волноводе, для которых l0>lкр, называются закритическими. Понятие критической длинны волны таким же образом вводится для волн высших типов. Постоянную b, называемую постоянной распространения или продольным волновым числом для волновода, можно представить в виде
где Vф - фазовая скорость распространения волны данного типа в волноводе; С0 - скорость света в свободном пространстве; f - частота электромагнитного колебания; fкр=C0/lкр - критическая частота волны данного типа. Из этого выражения можно определить фазовую скорость. Для волны типа Н10
Отсюда следует, что фазовая скорость в волноводе является функцией частоты электромагнитного колебания. Такое явление получило название дисперсии. На рис.5 показаны дисперсионные характеристики прямоугольного волновода для основного в первых высших типов колебаний. Наличие дисперсии приводит к нелинейным искажениям сигналов, передаваемых по волноводу, при достаточно большой ширине спектра радиосигналов. Но в некоторых СВЧ устройствах, например, в антенных решетках с частотным сканированием, явление дисперсии является полезным и используется в работе устройств. Дисперсию можно исследовать, получая в волноводе режим стоячих волн. Тогда поле в волноводе можно представить в виде наложения падающей и отраженной волн
в соответствии с (5) амплитуда поля в волноводе будет функцией Z и изменяется, как показано на рис.6, причем расстояние между соседними нулевыми значениями амплитуды равно lb/2. Измеряя при помощи измерительной линии расстояние между соседними минимумами поля в волноводе, можно построить эмпирическую дисперсионную характеристику волновода.
Рис.5. Дисперсионные характеристики прямоугольного волновода.
Рис.6. График изменения амплитуды стоячей волны.
Реальные волноводы изготавливаются из материалов, имеющих конечную величину проводимости. Поэтому токи проводимости, протекающие по стенкам волновода, частично преобразуют энергию электромагнитного поля в тепловую энергию, и по мере движения по волноводу энергия поля уменьшается (затухает). При этом одновременно уменьшаются амплитуды всех составляющих поля. С учетом затухания выражения (2) для волны основного типа преобразуются к виду
Мощность, переносимая по волноводу, будет описываться формулой
Здесь a - постоянная затухания, измеряемая в (дб/м) или в (неп/м), показывающая насколько децибел или непер уменьшится амплитуда волны при прохождении волновода длиной 1м. Приближенное теоретическое выражение для расчета постоянной затухания волны основного типа имеет вид
где Rn- поверхностное сопротивление стенки волновода. На рис.7 построены графики, показывающие изменения постоянных затухания волн низших типов в прямоугольном волноводе в зависимости от частоты. Постоянные затухания имеют минимум на некоторых частотах. При увеличении частоты постоянные затухания возрастают за счет Rn, так как начинает сильнее сказываться поверхностный эффект. При уменьшении частоты постоянные затухания увеличиваются из-за приближения к закритической области.
Рис. 7. Частотные зависимости постоянных затухания для прямоугольного волновода.
В действительности, затухание поля в волноводе вызывается и другими причинами, к которым относятся поглощение энергии поля в среде, заполняющей волновод, передача части энергии колебания других типов в волноводе и т.д. поэтому реальная величина постоянной затухания превосходит рассчитанную по (3). Для точного определения постоянной затухания прибегают к измерениям. Для измерений можно использовать замкнутый на конце волновод, присоединенный к измерительной линии. В измерительной линии будут действовать две волны: падающая, идущая в волноводе, и отраженная от короткозамкнутого конца волновода. Обозначим через Е0 амплитуду падающей волны в измерительной линии. За счет затухания в волноводе поля у короткозамыкателя будет иметь амплитуду Е0exp(-al), где l- длина волновода между короткозамыкателем и зондом измерительной линии. Волна, отраженная от короткозамыкателя, еще раз проходит через волновод и в измерительной линии ее амплитуда равна E0exp(-2al). Определяя при помощи измерительной линии коэффициент стоячей волны в тракте (КСВ), равный отношению максимальной амплитуды волны в волноводе измерительной линии к минимальной амплитуде, получим:
Отсюда
В реальных волноводах постоянная затухания достаточно мала, поэтому можно записать приближенное выражение
Порядок выполнения работы
Включить аппаратуру установки согласно инструкциям по эксплуатации используемых приборов, прогреть аппаратуру в течении 10 - 15 мин. Настроить генератор на частоту 10 ГГц. На указанной частоте настроить генератор на максимальную выходную мощность. Регулировкой аттенюатора А1 установить нулевые показания на его шкале. Убедиться, что при этом показания индикаторного прибора зависят от уровня СВЧ мощности.
1. Изучение картины поля стоячей волны основного типа в прямоугольном волноводе. 1.1. Переместить зонд измерительной линии в пучность стоячей волны в волноводе. Регулировками, имеющимися на измерительной линии, получить максимальные показания на индикаторе. Регулировками индикатора установить стрелку прибора на 80 - 90 делений шкалы. Переместить зонд измерительной линии в узел стоячей волны. 1.2. Производить отсчет показаний по измерительному усилителю, перемещая зонд измерительной линии вдоль волновода. Измерения производить с шагом 2 мм до следующего узла стоячей волны. Результаты измерений свести в таблицу 1.
Таблица 1
1.3. Переместить зонд измерительной линии в пучность стоячей волны. Вводить в волновод пластину аттенюатора А1 с шагом 1 мм и для каждого значения погружения пластины производить отсчет показаний индикатора. Результаты измерений свести в таблицу 2.
Таблица 2
2. Изучение дисперсии и затухания волны основного типа в прямоугольном волноводе. 2.1. Установить нулевые показания по шкале аттенюатора А1. 2.2. Отсчитать показания индикаторного прибора, при условии, что зонд измерительной линии находится в пучности стоячей волны. Переместить зонд измерительной линии в узел стоячей волны и, используя переключатель пределов измерения индикатора, отсчитать показания индикаторного прибора. Данные занести в таблицу 3. Переключатель пределов измерения индикатора вернуть в первоначальное положение.
Таблица 3
2.3. Отсчитать показания l1 по шкале измерительной линии, при условии, что зонд измерительной линии находится в узле стоячей волны. Переместить зонд в соседний узел стоячей волны. Положения зонда контролировать по индикатору. Отсчитать новое положение l2 по шкале измерительной линии. Данные занести в таблицу 4. 2.4. Настроить генератор на другую частоту, указанную в таблице 3. Настроить генератор на максимальную мощность на этой частоте. Настроить измерительную линию. Проделать п. 2.2. - п. 2.4. Выполнять измерения для всех частот, указанных в таблице 3.
Таблица 4
Содержание отчета
1. Цель работы. 2. Функциональная схема установки. 3. Таблицы с экспериментальными результатами и расчетами. 4. Графики, построенные по данным таблиц 1 - 4. 5. Дисперсионную характеристику волновода, построенную по (4) для частот, указанных в таблице 3. 6. График для постоянной затухания, построенный по (8) для частот, указанных в таблице 3. 7. Выводы по проделанной работе.
Контрольные вопросы
1. Нарисовать картину силовых линий для волны Н10 в прямоугольном волноводе. 2. Нарисовать графики, показывающие изменение амплитуд составляющих волны Н10 в зависимости от поперечных координат. 3. Дать понятие критической длинны волны основного типа. 4. Нарисовать и объяснить дисперсионную характеристику для волны основного типа. 5. Рассчитать размеры волновода так, чтобы в нем могла распространяться только волна Н10 в диапазоне частот 5 - 7 ГГц. 6. Как можно измерить дисперсионную характеристику волновода? 7. Объяснить причины затухания электромагнитных волн в волноводе. 8. Как можно измерить постоянную затухания волновода?
Список литературы
1. Лебедев И. В. Техника и приборы СВЧ. М., «Высшая школа», т.1, 1970. 2. Вольман В. И., Пименов О. В. Техническая электродинамика. М., «Связь», 1971. 3. Красюк Н. П., Дымович Н. Д. Электродинамика и распространение радио волн. М., «Высшая школа», 1974.
Метод волноводных мостов
Этот метод основан на измерении фазового сдвига и затухания волны, проходящей через заполненный исследуемым материалом участок волновода.
В данной схеме энергия генератора делится на две равные части, одна из которых идет в верхнее плечо моста, содержащего образец толщиной d. В другом плече находится калибровочный аттенюатор и фазовращатель, служащие для установления нулевого баланса индикаторного прибора. Процесс измерения состоит в установлении нулевого баланса сначала без образца, а затем с образцом. Измеряемые величины, которые являются разностью соответствующих показаний фазовращателя и аттенюатора, позволяют вычислить действительную и мнимую части диэлектрической проницаемости материала образца. Экспериментальная часть Описание установки Генератор СВЧ возбуждает электромагнитные волны в волноводе, в качестве которого используется волновод измерительной линии.
Чтобы измерительная линия, представляющая в режиме стоячей волны реактивную нагрузку, не влияла на работу генератора, она подключается через аттенюатор (отрезок волновода, в который погружается пластина, поглощающая СВЧ мощность). Измерение рекомендуется проводить в положении аттенюатора 10 дБ. Обычно генератор имеет собственный аттенюатор. Исследуемый диэлектрик помещен в отрезок волновода. Положение максимума поля относительно диэлектрика регулируется короткозамыкателем.
Определение Определение производится сочетанием методов холостого хода и короткого замыкания. При этом используется соотношение (12)
Для этого сначала берется пустой отрезок волновода, закорачивается пластиной. Затем измеряется длина волны в волноводе
Смещение максимума и длины волны в волноводе позволяет определить:
Затем короткозамыкатель устанавливается на расстояние Таким образом, зная
Контрольные вопросы 1. Запишите уравнения Максвелла для диэлектрика. 2. Что такое комплексная диэлектрическая проницаемость? Каков ее физический смысл. 3. Что такое 4. Каков критерий разделения сред на проводники и диэлектрики? 5. Охарактеризуйте методы измерения диэлектрической проницаемости? 6. В чем отличие метода полного заполнения сечения во
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 549; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.17.75 (0.019 с.) |


 (4) (4’)
(4) (4’) . На практике для определения чаще всего используют выражение (4), поэтому ниже под коэффициентом отражения мы будем понимать
. На практике для определения чаще всего используют выражение (4), поэтому ниже под коэффициентом отражения мы будем понимать  .
. (5)
(5) (6)
(6) , а
, а  ,
,
 ,
,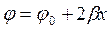 (6*),
(6*),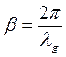 -фазовая постоянная, или волновое число для волновода,
-фазовая постоянная, или волновое число для волновода,  -длинна волны в волноводе.
-длинна волны в волноводе. (7)
(7) ,
,


 , (10)
, (10) . (11)
. (11) и фазы
и фазы  коэффициента отражения определить полные сопротивления нагрузок по формуле (18) и с помощью круговой номограммы. R =50 Ом (Z0)
коэффициента отражения определить полные сопротивления нагрузок по формуле (18) и с помощью круговой номограммы. R =50 Ом (Z0)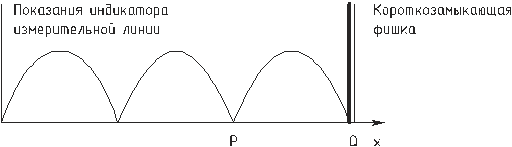

 , т.е. модуль коэффициента отражения
, т.е. модуль коэффициента отражения 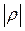 и фазу
и фазу  в «месте нахождения» нагрузки. Для этого короткозамыкающая фишка удаляется и в место её подключается исследуемая нагрузка (фиксированный аттенюатор, штыревая антенна и прочее). В этом случае эпюра стоячих волн изменится, и будет выглядеть примерно как на рисунке 9.
в «месте нахождения» нагрузки. Для этого короткозамыкающая фишка удаляется и в место её подключается исследуемая нагрузка (фиксированный аттенюатор, штыревая антенна и прочее). В этом случае эпюра стоячих волн изменится, и будет выглядеть примерно как на рисунке 9.
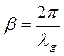 , а dmin – расстояние от нагрузки до ближайшего минимума, (рис. 9).
, а dmin – расстояние от нагрузки до ближайшего минимума, (рис. 9).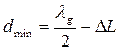 . (21)
. (21) подставляем в формулу (18), чем и определяем искомое комплексное сопротивление нагрузки.
подставляем в формулу (18), чем и определяем искомое комплексное сопротивление нагрузки.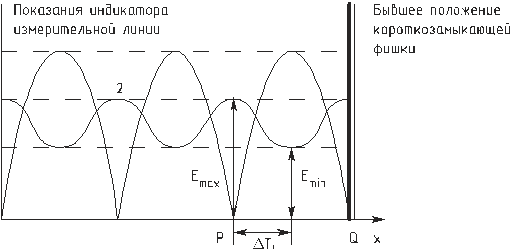
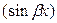 от
от 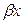 наносятся экспериментальные точки (рис. 8) с учётом квадратичной характеристики детектора, т.е. пропорциональности показаний индикатора квадрату напряженности поля.
наносятся экспериментальные точки (рис. 8) с учётом квадратичной характеристики детектора, т.е. пропорциональности показаний индикатора квадрату напряженности поля.
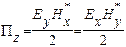 (1)
(1)
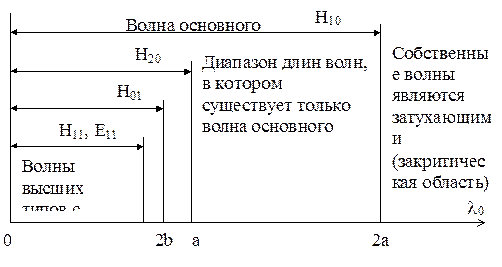
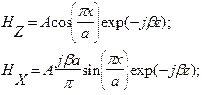

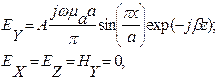 (2)
(2)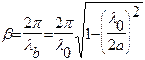

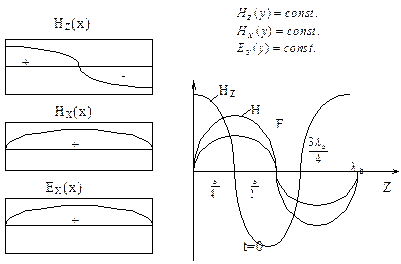
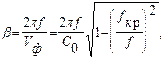 (3)
(3)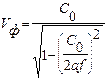 (4)
(4)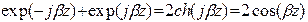 (5)
(5)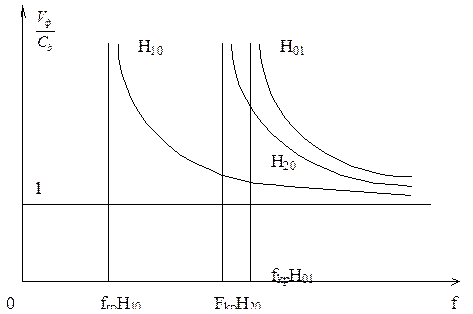
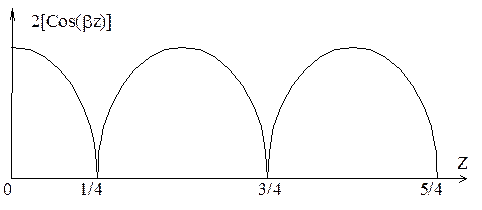
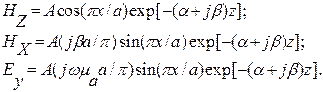 (6)
(6)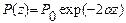 (7)
(7)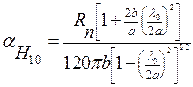 [неп/м], (8)
[неп/м], (8)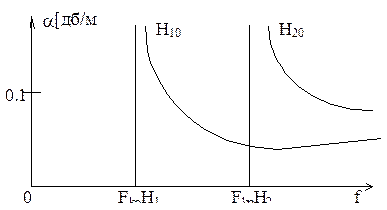
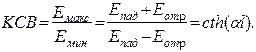 (9)
(9)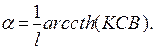
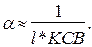 (10)
(10)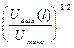
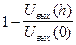
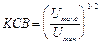




 и координата любого максимума поля стоячей волны. После этого на месте пустого отрезка волновода ставится отрезок с диэлектриком известной толщины. Измеряется смещение максимума
и координата любого максимума поля стоячей волны. После этого на месте пустого отрезка волновода ставится отрезок с диэлектриком известной толщины. Измеряется смещение максимума  и коэффициент бегущей волны:
и коэффициент бегущей волны: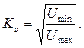

 от образца, и измеряются те же параметры, что и в первом случае.
от образца, и измеряются те же параметры, что и в первом случае. можно решить уравнение (12), что дает возможность определить
можно решить уравнение (12), что дает возможность определить  .
.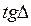 ?
?


