
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение полных сопротивлений и измерение длины волны в волноводеСодержание книги
Поиск на нашем сайте
Цель работы
Приборы и принадлежности 1. Генератор дециметрового диапазона ГЗ-10А. 2. Измерительная коаксиальная линия. 3. Милливольтметр. 4. Согласованная нагрузка. 5. Развязывающий аттенюатор. 6. Короткозамыкающая заглушка. 7. Исследуемые нагрузки. Краткая теория метода Основные понятия о характеристиках процессов в линии передачи В зависимости от возмущения электромагнитной волны в волноводе подразделяются на волны типа Е=ТМ – плоские магнитные волны, в которых отсутствует продольная составляющая магнитного поля Н, и волны типа Н=ТЕ – при отсутствии продольной составляющей электрического поля Е. В коаксиальных измерительных линиях чаще всего используется плоская волна типа ТЕМ, не имеющая продольных компонентов Е и Н. Электрические силовые линии направлены радиально от центрального проводника к внешнему, а магнитные – концентрическими окружностями вокруг центрального провода. Возьмем измерительную линию, слева присоединенную к генератору СВЧ а справа к измеряемой нагрузке (рис. 1). направим ось х от генератора к нагрузке вдоль измерительной линии с началом отсчета в некоторой точке х =0.
рис. 1 При включении генератора в волноводе измерительной линии установятся стоячие волны, так как часть энергии поля будет отражаться от нагрузки. Поперечные составляющие полей Е и Н могут быть представлены как сумма падающей и отраженной волн (т.е. идущей в положительном направлении Е+ и в отрицательном Е- соответственно): Е=Е++Е-, (3) Н=Н++Н-. (3’) Коэффициентом отражения ρ в данной точку волновода называется комплексная величина, равная отношению взятых в этой точке поперечных составляющих Е и Н:
При этом Коэффициент отражения зависит от точки, в которой он определяется, так как при перемещении по волноводу фазы волн изменяются. в самом деле, для начала отсчета (точки 0):
а любой другой точки для волновода без потерь:
но поэтому
и мы получим:
Здесь Характеристическим или волновым сопротивлением волновода Z0 называется отношение поперечных компонент полей Е и Н для бегущей волны:
Оно является неизменным для любой точки. Полным сопротивлением волновода в данной точке называют комплексную величину, равную отношению полей (3) и (3*):
или учитывая (4), (4*) и (7),
Таким образом, для определения полного сопротивления в данной точке волновода необходимо измерить в ней коэффициент отражения ρ. Для измерения модуля ρ достаточно измерить коэффициент бегущей волны S (КБВ) или обратную ему величину – коэффициент стоячей волны (КСВ). Коэффициентом стоячей волны называют отношение напряженностей полей в точках минимума (Еmin) и максимума (Emax) электрического поля (рис.1)
Процесс образования в волноводе стоячих волн для некоторой точки удобно представить графически:
Рис. 2 Из рис. 2 видно, что картина стоячих волн получится в согласии с рис. 1, если вектор Е- вращать против часовой стрелки. Из этих же рисунков ясно, что
Если из эксперимента известны Еmin и Emax, то используя (10), можно определить модуль коэффициента отражения:
Для определения фазы коэффициента отражения достаточно измерить расстояние данной точки от ближайшего минимума, где фаза принимается равной (2n-1)π. Тогда для точки минимума по (6): φ=φ0+2βxmin=(2n-1) π, откуда: φ0=(2n-1)π -2βxmin, и для точки х, в которых нужно определить фазу, будем иметь φ=(2n-1) π -2βxmin+2βx=(2n-1) π -2β(х-хmin), (12) Принимаем условие, при котором φ всегда расположено в интервале между - π и + π, тогда n=0. Обозначая х-хmin=dmin, окончательно получим: φ=-2βdmin- π, (13) На практике определяют обычно местоположение минимума и измеряют расстояние до него со стороны нагрузки, а не со стороны источника.
|
||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.62.5 (0.007 с.) |


 (4) (4’)
(4) (4’) . На практике для определения чаще всего используют выражение (4), поэтому ниже под коэффициентом отражения мы будем понимать
. На практике для определения чаще всего используют выражение (4), поэтому ниже под коэффициентом отражения мы будем понимать  .
. (5)
(5) (6)
(6) , а
, а  ,
,
 ,
,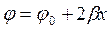 (6*),
(6*),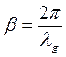 -фазовая постоянная, или волновое число для волновода,
-фазовая постоянная, или волновое число для волновода,  -длинна волны в волноводе.
-длинна волны в волноводе. (7)
(7) ,
,


 , (10)
, (10) . (11)
. (11)


