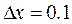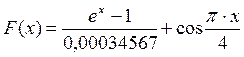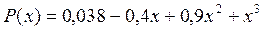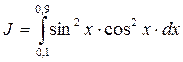Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Scilab-5.1.1. Работа в диалоговом режимеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ИНФОРМАТИКА
Лабораторный практикум
Часть VI
Изучение системы компьютерных вычислений в Scilab
МОСКВА 2010
Составители: А.В. Захаров, ст. преп. (разд. 3), И.М. Шаронова, доц., канд. техн. наук (разд. 1,2)
Под редакцией проф., д-ра физ.-мат. наук В.В. Серова
Информатика: Лаб. практикум. Ч. 6 / Российск. заочн. ин-т текстил. и легк. пр-сти; Сост. В.А. Захаров, И.М. Шаронова. М., 2010. …. с.
Предназначено для студентов всех специальностей.
Редактор О.Л.Лобанова План 2010г., поз..
Сдано в производство. Формат 60х84/16. Бумага офсетная. Печать офсетная. Усл. печ. Л_____. Уч.-изд. л. ____Тираж 100 экз. Заказ. Цена договорная.
Российский заочный институт текстильной и легкой промышленности. 123423 Москва ул. Демьяна Бедного, 7. Введение Для решения инженерных и экономических задач были созданы языки программирования Бейсик, Фортран, Паскаль, Кобол и другие. Но разработка программы на любом из этих языков требует определенной подготовки, а также немалых затрат времени и труда. Начиная с 60-х годов прошлого столетия, параллельно с языками программирования развивались системы компьютерной математики. Эти пакеты программ позволяют получить решение многих задач в численном или символьном виде в диалоговом режиме даже без программирования. Кроме того, каждый из этих комплексов программ имеет свой язык программирования, предназначенный для решения очень сложных технических и экономических проблем. Современные системы компьютерной математики Mathcad, Maple, Mathematica, Matlab обладают такой вычислительной мощью, о которой инженеры и экономисты еще несколько десятилетий тому назад могли только мечтать. Все вышеперечисленные пакеты программ обладают широкими графическими возможностями, способны выполнять символьные преобразования математических выражений. Однако, поскольку значительная часть пользователей нуждается только в простом помошнике-вычислителе, эти системы спроектированы так, что методы решения сложных проблем, если они не используются, никак себя не проявляют. Пакет Mathcad прост в использовании и легок в изучении, а математические выражения и формулы записываются в нем так, как это принято в алгебре, например:
Широкое распространение среди инженеров и научных работников получила система компьютерной математики Matlab. По утверждению разработчиков этой системы студенты более чем 3500 ведущих зарубежных университетов изучают этот пакет программ. Язык программирования, созданный для первых версий Matlab, очень прост и не вызывает никаких затруднений при изучении. В более поздних версиях пакета в этот язык добавлены новые конструкции, которые позволяют опытным пользователям разрабатывать объектно-ориентированные приложения, работать с многопроцессорными системами, использовать программы, написанные на других языках. Система Matlab может быть использована в диалоговом режиме. В этом режиме она представляет собой чрезвычайно мощный калькулятор, которому доступны и вызов огромного количества функций, и построение графиков. Коммерческая система Matlab создавалась специально для моделирования сложных технических объектов, для проведения сложных расчетов, в которых используются вектора, матрицы, комплексные числа. Поэтому основным типом данных в этой системе является матрица, а графики зависимости функций от их аргументов создаются системой Matlab в форме, используемой в инженерной документации. К сожалению, комплексы программ Mathcad, Maple, Mathematica, Matlab – коммерческие и очень дорогие пакеты. Однако в Интернете можно найти свободно распространяемые их аналоги, которые разрабатываются энтузиастами. В этих разработках участвуют и некоторые коммерческие фирмы. Однако, имеющаяся в Интернете документация к свободно распространяемым пакетам представлена в основном на английском языке. Для свободно распространяемой системы Scilab (аналога Matlab) имеется довольно обширная документация на русском языке. В этой системе применяется интерфейс подобный интерфейсу Matlab и практически тот же язык программирования. Многие команды, используемые для решения задач вычислительной математики, построения графиков имеют названия те же или схожие с названиями соответствующих команд Matlab. Система Scilab разрабатывалась для OC Linux. В настоящее время доступны последние версии этой системы для Windows. Их можно загрузить на сайте http://www.scilab.org. Далее рассматриваются некоторые вопросы использования Scilab для решения вычислительных задач.
Командное окно После запуска Scilab на экране появится окно системы (рис.1). Вид окна зависит от версии программы и настроек. Обычно оно содержит строку меню, панель инструментов и командное окно. Пользователь вводит операторы (команды) в строке, которая начинается с символа -->, за которым следует мигающий курсор (приглашения начать ввод). Эта строка называется командной. Для выполнения введенного оператора следует нажать клавишу Ente r. Мигающий курсор переместится ниже и, если введенная команда не заканчивается символом «точка с запятой», результат расчета будет выведен на экран. Записанный в конце оператора символ «точка с запятой» подавляет вывод результата расчета. Целая часть числа отделяется от дробной части точкой. Пример 1.1. Вычислить функцию -->x=0.5 x = 0.5 -->y=1.05; -->z=x+y z = 1.55 Для редактирования и выполнения введенной ранее команды необходимо скопировать ее в командную строку. Присвоенные переменным значения сохраняются в специальной области памяти. Для очистки значений всех переменных в этой области используется команды clear, а для очистки значения одной или нескольких переменных - clear имя или список разделенных запятыми имен, например, clear x, y
Рис. 1.1. Командное окно программы
В Scilab можно вычислять и выводить в командное окно не только значения переменных или функций, но и значения выражений. Результат вычисления выражения присваивается системной переменной ans, которую можно использовать в других выражениях. Пример 1.2. Вычислить значение выражения -->x=2.5; -->x^2 // вычисляется значение выражения ans = // ответ 6.25 //ans - первые символы английского слова answer (ответ, решение) -->ans=ans+1 // используется ответ 7.25 Записанные в программе подряд два символа / (слэш) служат признаком комментария. В Scilab разрешается размещать в одной строке несколько операторов (команд). Каждый из них, за исключением последнего, должен заканчиваться символом «точка с запятой». Пример 1.3. -->x=0.25; y=1.2; z=2*y-x z = 2.15 В системе имеется много подпрограмм, предназначенных для вычисления математических функций. Некоторые из них перечислены в представленной ниже таблице (Таблица 1). Для вызова функции следует записать ее имя, а за ним, в круглых скобках – аргумент или аргументы. Между именем функции и скобкой не должно быть ни пробелов, ни каких-либо символов. Таблица 1
Для часто используемых констант, называемых системными переменными, применяются специальные обозначения. Некоторые из них приведены ниже. %pi – число π %е – число e (2.7182818) %i - мнимая единица %NaN – неопределенный результат, например, 0/0.
Пример 1.4. Вычислить значение функции f, если х =0,25.
Решение: ->x=0.25; ->f=(x^2+cos(%pi*x/4))/(1+%e^x) // знаменатель может быть записан f = // в виде: (1+exp(x)) 0.4567748 Используемое в программе имя переменной не должно содержать более 24 символов. Регистр букв в имени имеет значение: ab, Ab, aB, AB – разные имена. В отличие от VBA, в именах переменных буквы русского алфавита не допускаются. Вектора и матрицы Основным типом данных в системе Scilab является матрица – двумерная таблица с заданным количеством строк и столбцов.
В Scilab столбец или строку матрицы называют вектором. Вектор – матрица, состоящая из одного столбца или одной строки. Скаляр – матрица, в которой имеется один столбец и одна строка. Элементы матрицы могут быть целыми, вещественными или комплексными числами, могут быть и переменными других типов. Один из способов задания векторов и матриц - это их поэлементная запись в операторе присваивания. Все элементы вектора или матрицы заключаются в квадратные скобки и разделяются пробелами или запятыми. -->X=[3 9 5 4] X = 3. 9. 5. 4. Элементы матрицы перечисляются в квадратных скобках строка за строкой. Строки в матрицах и в векторах-столбцах заканчиваются символом «точка с запятой». -->Z=[1,2;3,4] // матрица Z = 1. 2. 3. 4. -->Y=[0;1] // вектор-столбец Y = 0. 1. Если вектор-строка представляет собой арифметическую прогрессию, то ее элементы можно задать следующим образом:
Здесь Результат вычисления элементарной функции от вектора, также представляет собой вектор. Пример 1.5. Вычислить значения функции y=sin(x), если х изменяется от 0 до 1 с шагом dx, равным 0,1. -->x=0:0.1:0.5 x = 0. 0.1 0.2 0.3 0.4 0.5 -->y=sin(x) y = 0. 0.0998334 0.1986693 0.2955202 0.3894183 0.4794255 Если параметр dx в операторе задания вектора-строки отсутствует, то по умолчанию он принимается равным единице. -->w=1:5 w = 1. 2. 3. 4. 5. Для записи арифметических операций в выражении используются перечисленные ниже обозначения. · Сложение и вычитание матриц, векторов, скаляров: + и -; · Умножение и деление скаляров, алгебраическое перемножение матриц: символы * и /; · Возведение в степень скаляров и матриц: ^; Квадратную матрицу можно возводить только в целую степень. Для работы с элементами векторов и матриц введены специальные операции. · Поэлементное умножение векторов или матриц одного размера: .* · Поэлементное деление: ./ · Поэлементное возведение в степень: .^ Символ «’» (апостроф, одиночная кавычка) означает транспонирование. В результате выполнения операции алгебраического умножения вектора-столбца на вектор-строку получается число. В результате выполнения операции алгебраического умножения вектора-столбца на вектор-строку получается матрица. Пример 1.6. Дан вектор-столбец В. Записать его в виде вектора строки В1. Вычислить алгебраические произведения В и В1, В1 и В, а также поэлементное произведение В и В1. -->B=[1; 3; 4; 5] // это вектор-столбец! B = 1. 3. 4. 5. -->B1=B' // транспонирование вектора-столбца В B1 = 1. 3. 4. 5. // это вектор-строка! -->B*B1 // умножение столбца на строку – получается матрица ans = 1. 3. 4. 5. 3. 9. 12. 15. 4. 12. 16. 20. 5. 15. 20. 25. -->B1*B // умножение строки на столбец - получается число ans = 51. -->B.*B1’ // Поэлементное умножение векторов В и В1’ ans = 1. // это вектор-столбец! 9. 16. 25. Допускается поэлементное умножение только векторов одинаковой длины или матриц одного разиера. Для определения размера матрицы или вектора можно использовать команду size(имя): -->size(B) ans = 4. 1. // эта матрица (вектор-столбец) содержит 4 строки и 1 столбец Plot(x,y) Здесь x – массив значений аргумента, y – массив значений функции. Пример 1.6. Для аргумента х, изменяющегося от 0 до 1 с шагом 0.01, вычислить значения функции -->x=0:0.01:1; -->y=cos(10*x); // Вычисление функции у -->plot(x,y) // Построение графика
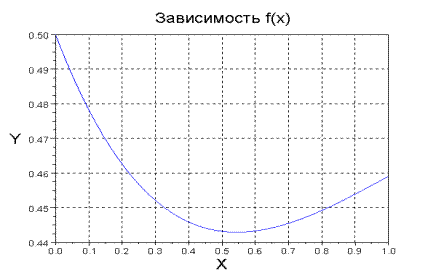
Рис. 1.2. График функции Пример 1.7. Для аргумента х, изменяющегося от 0 до 1 с шагом 0.01, вычислить значения функции f и построить график зависимости функции f от x (рис. 1.3).
Вид графика улучшится, если для вывода сетки использовать оператор Xgrid() Для вывода заголовка графика, надписей у осей используется оператор xtitle(‘Заголовок графика','ось X','ось Y') Решение -->x=0:0.01:1; -->f=(x.^2+cos(%pi.*x./4))./(1+exp(x)); -->plot(x,f) -->xgrid() // вывод сетки -->xtitle('Зависимость f(x)','X','Y') // вывод надписей Записанные подряд два символа / (слэш) служат признаком комментария.
Рис. 1.3. График функции f=(x.^2+cos(%pi.*x./4))./(1+exp(x));
Вычисление определителя Для вычисления определителя матрицы используется функция det(имя). ->A=[2 3 7 6; 3 5 3 1; 5 3 1 3; 3 3 1 6] A = 2. 3. 7. 6. 3. 5. 3. 1. 5. 3. 1. 3. 3. 3. 1. 6. -->W=det(A) W = - 420.
Определение корней полинома Полиномом называется многочлен:
Для создания полинома следует перечислить в квадратных скобках все его коэффициенты (по возрастанию степени х), например, y=[1 2 3] Затем следует вызвать функцию poly(y,’x’,’c’). Здесь параметр ‘с’ означает, что полином строится по заданным его коэффициентам. Пример. -->y=[1 2 3]; -->P=poly(y,'x','c') P = 1 + 2x + 3x Для вычисления корней полинома используется функция roots(P) Здесь P - определенный с помощью функции poly полином. Вычисляются как действительные, так и комплексные корни полинома.
Пример 1.12. Вычислить корни полинома -->P=poly([-1 0.6 0.4 1],'x','c') P = 2 3 - 1 + 0.6x + 0.4x + x -->roots(P) ans = 0.7153636 - 0.5576818 + 1.0425361i - 0.5576818 - 1.0425361i Пример 1.13. Найти все корни уравнения -->Y=poly([0.139104 -0.7044 -0.01 1],'x','c') Y = 2 3 0.139104 - 0.7044x - 0.01x + x -->Korny=roots(Y) Korny = 0.21 0.72 - 0.92 Условный оператор Как правило, линейные алгоритмы и программы используются в процессе обучения для приобретения навыков работы с арифметическими выражениями, стандартными функциями, операторами ввода-вывода. На практике гораздо чаще применяются программы, в которых реализованы разветвляющиеся алгоритмы. В них кроме вычисления функций имеет место проверка различных условий. В зависимости от результата проверки расчеты выполняются по тем или иным формулам, т.е. работают те или иные ветви алгоритма. Операторы программы выполняются в том порядке, в каком они записаны, один за другим, пока не дойдет очередь до одного из операторов управления, которые позволяют организовать многократное повторение группы операторов или осуществить переход к фрагменту, записанному в другой части программы. В Scilab имеется несколько операторов управления. Рассмотрим одну из форм условного оператора, который записывается в виде: if условие оператор или операторы Else оператор или операторы End Условие - это логическое выражение, которое может принимать только одно из двух значений: истина или ложь. Частным случаем логического выражения является отношение - операция сравнения двух величин. В таблице 2 приведены принятые в Scilab обозначения операций отношения. Оператор выполняется следующим образом. Вычисляется значение логического выражения (условия). Если это значение есть "истина", то выполняется оператор или группа операторов, записанных после условия, иначе управление работой программы передается операторам, которые следуют за служебным словом else. Заканчивается условный оператор служебным словом end. В случае необходимости можно разместить после условия или после служебного слова else несколько операторов, в качестве которых разрешается использовать операторы присваивания, цикла, ввода-вывода, а также другой оператор условного перехода. Таблица 2
Пример записи условного оператора. if x>0 a=1+x; else a=1; end Служебное слово else и следующие за ним оператор или операторы можно опустить. В этом случае условный оператор записывается в виде: if (условие) оператор или операторы End
Оператор цикла Решение задачи численными методами практически всегда включает в себя многократное повторение вычислений по одним и тем же формулам, но с различными числовыми данными. Эта часть называется циклом. Для организации цикла используется специальный оператор, который позволяет малым количеством операторов описать процесс выполнения большого объема вычислений и называется оператором цикла.. Оператор цикла состоит из заголовка, тела цикла, включающего один или несколько операторов, и завершается оператора end, который указывает, где именно заканчивается оператор цикла В теле цикла описывается фрагмент программы, который должен выполняться многократно. В языке программирования Scilab имеется несколько вариантов оператора цикла. Здесь рассматривается один из них. Заголовок этого оператора имеет вид: for x=x0: dx: xkon Здесь x - параметр цикла, переменная, величина которой изменяется от значения x0 до xkon с шагом dx. Если шаг изменения параметра цикла равен 1, то его можно не указывать в заголовке цикла. Тело цикла выполняется многократно при различных значениях параметра цикла. В случае, когда dx>0, оператор цикла выполняется следующим образом. Параметру цикла x присваивается значение x0. Затем проверяется условие x <= xk (*) Если значение этого отношения есть "истина", то выполняются операторы тела цикла, параметр цикла увеличивается на величину шага dx и снова проверяется условие (*). Если x > xk, то работа оператора цикла прекращается, и выполняется оператор, записанный за оператором цикла. Ниже приведена блок-схема, поясняющая работу оператора цикла.
Рис. 2.3. Блок-схема оператора цикла
Пример 2.2. Для аргумента х, изменяющегося от -1 до 1 с шагом dx =0.25, вычислить функцию:
где Текст программы i=1; // индекс элементов массивов, используемых при построении графика for x=-0.5:0.25:0.50001 // начало цикла if x>0 // начало условного оператора a=1+x; else a=1+x; end // конец условного оператора f=a*x; disp([x,f]) // вывод значений x и f в командное окно xgraf(i)=x; // создается массив значений х для построения графика fgraf(i)=f; // создается массив значений f для построения графика i=i+1; end // конец цикла plot(xgraf,fgraf) xgrid() xtitle('f=a*x','x','f') Результаты расчета (в командном окне) - 0.5 - 0.25 - 0.25 - 0.1875 0. 0. 0.25 0.3125 0.5 0.75
Рис. 2.4. График функции В приведенной программе для вывода результатов расчета в командное окно используется команда disp(имя). В этой команде в скобках указывается имя переменной или массива (только одного). При необходимости вывести значения нескольких переменных или массивов их заключают в квадратные скобки. График функции f(x) приведен на рисунке 2.4.
3. Решение задач вычислительной математики Для решения задач вычислительной математики применим редактор SciPad, как делали это в разделе 2. Открыть его можно, выбрав Инструменты в меню командного окна и команду Редактор – в открывшемся спускающемся списке (рис. 2.1). В окне SciPad создать новый файл с программой можно путем копирования из командного окна уже отлаженных операторов. По умолчанию создаваемому файлу присваивается имя Untitledx, где х - целое число, номер файла. Файл-сценарий можно сохранить, а потом открыть. Для запуска его на выполнение следует в меню окна выбрать команду Execute (рис. 2.2), а затем в спускающемся списке – команду Load into Scilab или Load all into Scilab.
Пример 3.4.
Программа для вычисления интеграла методом трапеций. t=0:0.1:%pi; Способ 3.
Синтаксис
Параметры Вычисляется Функция f задана в виде аналитической зависимости от v. Пример 3.5. Способ 4.
Синтаксис команды
Параметры Оценка точности вычислений: abs(I-v)<= max(ea,er*abs(I)), где I - точное значение интеграла.
Пример 3.6. Вычисление интеграла Программа deff('[F]=f(x)','F=x.^3+cos(x)') // программа в J=intg(0,1,f) // окне редактора
Результат J = // результат расчета в 1.091471 // командном окне Задания по выполнению лабораторной работы Задание 1. В ычислить значения функции 1.1 1.2 1.3 Задание 2. Найти корни полинома. 2.1. 2.2. 2.3. Задание 3. Решить нелинейное уравнение 3.1. 3.2. Задание 4. Вычислить определенный интеграл 4.1. 4.2. 4.3. Приложение. Примеры графиков
График функции
Литература 1. Е.Р. Алексеев, О.В. Чеснокова, Е.А. Рудченко. Scilab: Решение инженерных задач. – М.: ALT Linux; БИНОМ. Лаборатория знаний, 2008 2. М.И. Павлова. Руководство по работе с пакетом Scilab. http://www.csa/ru/~zebra/my-scilab/index/html 3. И.С. Тропин, О.И. Михайлова, А.В. Михайлов. Численные и технические расчеты в среде Scilab. Учебное пособие. – Москва: 2008, 65стр. (для школьников, Linux) http://www.unux/ru/static/MethodBooks-Scilab/Scilab/pdf 4. Е.Р. Алексеев. Scilab – теория и практика на русском языке. http://teacher.dn-ua.com/Math/Scilab/Scilab.html
Содержание Введение………………………………………………………………….. 3 1.Scilab-5.1.1. Работа в диалоговом режиме…………………………… 4 1.1. Командное окно…………………………………………………. 4 1.2. Вектора и матрицы……………………………………………… 7 1.3. Построение графиков на плоскости…………………………… 1.4. Вывод нескольких графиков в одном окне……………………. 1.5. Построение трехмерных графиков……………………………… 1.6. Решение некоторых задач линейной алгебры 1.6.1. Вычисление определителя………………………………….. 1.6.2. Линейные алгебраические уравнения……………………… 1.6.3. Определение корней полинома…………………………… 2. Разработка программы в Scilab……………………………………… 2.1. Использование редактора SciPad………………………………… 2.2 Условный оператор……………………………………………… 2.3. Оператор цикла……………………………………………………. 3. Решение задач вычислительной математики в окне редактора…… 3.1. Решение нелинейных уравнений………………………………… 3.2. Вычисление определенного интеграла …………………………. Задания по выполнению лабораторной работы………………………… Приложение. Примеры графиков………………………………………… Литература………………………………………………………………….
ИНФОРМАТИКА
Лабораторный практикум
Часть VI
Изучение системы компьютерных вычислений в Scilab
МОСКВА 2010
Составители: А.В. Захаров, ст. преп. (разд. 3), И.М. Шаронова, доц., канд. техн. наук (разд. 1,2)
Под редакцией проф., д-ра физ.-мат. наук В.В. Серова
Информатика: Лаб. практикум. Ч. 6 / Российск. заочн. ин-т текстил. и легк. пр-сти; Сост. В.А. Захаров, И.М. Шаронова. М., 2010. …. с.
Предназначено для студентов всех специальностей.
Редактор О.Л.Лобанова План 2010г., поз..
Сдано в производство. Формат 60х84/16. Бумага офсетная. Печать офсетная. Усл. печ. Л_____. Уч.-изд. л. ____Тираж 100 экз. Заказ. Цена договорная.
Российский заочный институт текстильной и легкой промышленности. 123423 Москва ул. Демьяна Бедного, 7. Введение Для решения инженерных и экономических задач были созданы языки программирования Бейсик, Фортран, Паскаль, Кобол и другие. Но разработка программы на любом из этих языков требует определенной подготовки, а также немалых затрат времени и труда. Начиная с 60-х годов прошлого столетия, параллельно с языками программирования развивались системы компьютерной математики. Эти пакеты программ позволяют получить решение многих задач в численном или символьном виде в диалоговом режиме даже без программирования. Кроме того, каждый из этих комплексов программ имеет свой язык программирования, предназначенный для решения очень сложных технических и экономических проблем. Современные системы компьютерной математики Mathcad, Maple, Mathematica, Matlab обладают такой вычислительной мощью, о которой инженеры и экономисты еще несколько десятилетий тому назад могли только мечтать. Все вышеперечисленные пакеты программ обладают широкими графическими возможностями, способны выполнять символьные преобразования математических выражений. Однако, поскольку значительная часть пользователей нуждается только в простом помошнике-вычислителе, эти системы спроектированы так, что методы решения сложных проблем, если они не используются, никак себя не проявляют. Пакет Mathcad прост в использовании и легок в изучении, а математические выражения и формулы записываются в нем так, как это принято в алгебре, например:
Широкое распространение среди инженеров и научных работников получила система компьютерной математики Matlab. По утверждению разработчиков этой системы студенты более чем 3500 ведущих зарубежных университетов изучают этот пакет программ. Язык программирования, созданный для первых версий Matlab, очень прост и не вызывает никаких затруднений при изучении. В более поздних версиях пакета в этот язык добавлены новые конструкции, которые позволяют опытным пользователям разрабатывать объектно-ориентированные приложения, работать с многопроцессорными системами, использовать программы, написанные на других языках. Система Matlab может быть использована в диалоговом режиме. В этом режиме она представляет собой чрезвычайно мощный калькулятор, которому доступны и вызов огромного количества функций, и построение графиков. Коммерческая система Matlab создавалась специально для моделирования сложных технических объектов, для проведения сложных расчетов, в которых используются вектора, матрицы, комплексные числа. Поэтому основным типом данных в этой системе является матрица, а графики зависимости функций от их аргументов создаются системой Matlab в форме, используемой в инженерной документации. К сожалению, комплексы программ Mathcad, Maple, Mathematica, Matlab – коммерческие и очень дорогие пакеты. Однако в Интернете можно найти свободно распространяемые их аналоги, которые разрабатываются энтузиастами. В этих разработках участвуют и некоторые коммерческие фирмы. Однако, имеющаяся в Интернете документация к свободно распространяемым пакетам представлена в основном на английском языке. Для свободно распространяемой системы Scilab (аналога Matlab) имеется довольно обширная документация на русском языке. В этой системе применяется интерфейс подобный интерфейсу Matlab и практически тот же язык программирования. Многие команды, используемые для решения задач вычислительной математики, построения графиков имеют названия те же или схожие с названиями соответствующих команд Matlab. Система Scilab разрабатывалась для OC Linux. В настоящее время доступны последние версии этой системы для Windows. Их можно загрузить на сайте http://www.scilab.org. Далее рассматриваются некоторые вопросы использования Scilab для решения вычислительных задач.
Scilab-5.1.1. Работа в диалоговом режиме Командное окно После запуска Scilab на экране появится окно системы (рис.1). Вид окна зависит от версии программы и настроек. Обычно оно содержит строку меню, панель инструментов и командное окно. Пользователь вводит операторы (команды) в строке, которая начинается с символа -->, за которым следует мигающий курсор (приглашения начать ввод). Эта строка называется командной. Для выполнения введенного оператора следует нажать клавишу Ente r. Мигающий курсор переместится ниже и, если введенная команда не заканчивается символом «точка с запятой», результат расчета будет выведен на экран. Записанный в конце оператора символ «точка с запятой» подавляет вывод результата расчета. Целая часть числа отделяется от дробной части точкой. Пример 1.1. Вычислить функцию -->x=0.5 x = 0.5 -->y=1.05; -->z=x+y z = 1.55 Для редактирования и выполнения введенной ранее команды необходимо скопировать ее в командную строку. Присвоенные переменным значения сохраняются в специальной области памяти. Для очистки значений всех переменных в этой области используется команды clear, а для очистки значения одной или нескольких переменных - clear имя или список разделенных запятыми имен, например, clear x, y
Рис. 1.1. Командное окно программы
В Scilab можно вычислять и выводить в командное окно не только значения переменных или функций, но и значения выражений. Результат вычисления выражения присваивается системной переменной ans, которую можно использовать в других выражениях. Пример 1.2. Вычислить значение выражения -->x=2.5; -->x^2 // вычисляется значение выражения ans = // ответ 6.25 //ans - первые символы английского слова answer (ответ, решение) -->ans=ans+1 // используется ответ 7.25 Записанные в программе подряд два символа / (слэш) служат признаком комментария. В Scilab разрешается размещать в одной строке несколько операторов (команд). Каждый из них, за исключением последнего, должен заканчиваться символом «точка с запятой». Пример 1.3. -->x=0.25; y=1.2; z=2*y-x z = 2.15 В системе имеется много подпрограмм, предназначенных для вычисления математических функций. Некоторые из них перечислены в представленной ниже таблице (Таблица 1). Для вызова функции следует записать ее имя, а за ним, в круглых скобках – аргумент или аргументы. Между именем функции и скобкой не должно быть ни пробелов, ни каких-либо символов. Таблица 1
|
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 911; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.02 с.) |


 , если
, если 



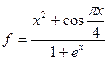


 - начальное значение х,
- начальное значение х, 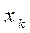 - конечное, а параметр dx - шаг прогрессии.
- конечное, а параметр dx - шаг прогрессии. и построить график зависимости функции y отаргумента x (рис. 1.2).
и построить график зависимости функции y отаргумента x (рис. 1.2).





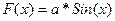 ,
,

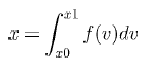
 .
. и построить график зависимости
и построить график зависимости  от
от  . Аргумент
. Аргумент