Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение трехмерных графиковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При построении поверхности z(x,y) вначале создается прямоугольная сетка на плоскости. Для ее формирования используется функция meshgrid(x,y).
или
Для построения поверхности можно использовать функции serf(x,y,z), mesh(x,y,z). Первая строит поверхность, заливая каждую ячейку цветом, который зависит от значения функции в узле сетки, а вторая заливает поверхность одним цветом. Пример 1.9. Построить график функции -->[x,y]=meshgrid(-2:0.05:2,-3:0.05:3); -->z=5*y.^2-x.^2; -->surf(x,y,z); -->xgrid() Пример 1.10. Построение поверхности (рис. 1.5) с помощью функции mesh(x,y,z) -->[x,y]=meshgrid(-2:0.05:2,-3:0.05:3); -->z=5*y.^2-x.^2; -->mesh(x,y,z) -->xgrid() -->xtitle('Использована функция mesh ','X','Y','Z') С помощью команд mesh(x,y,z) и surf(x,y,z) можно построить в одном окне несколько поверхностей. Имеются и другие функции, которые применяются для создания трехмерных графиков. В Scilab имеются программы построения кривых и поверхностей, заданных параметрически, построения линий уровня (изолиний), гистограмм, имеется возможность вручную редактировать графики, изменяя многие их параметры, например, размер и цвет используемых шрифтов.
Рис. 1.5. График функции z=5*y.^2-x.^2;
1.6. Решение некоторых задач линейной алгебры в диалоговом Вычисление определителя Для вычисления определителя матрицы используется функция det(имя). ->A=[2 3 7 6; 3 5 3 1; 5 3 1 3; 3 3 1 6] A = 2. 3. 7. 6. 3. 5. 3. 1. 5. 3. 1. 3. 3. 3. 1. 6. -->W=det(A) W = - 420.
Линейные алгебраические уравнения Пример 1.11.. Решить систему линейных алгебраических уравнений
Запишем эту систему в матричном виде: AX=B (*).
Умножим слева на Обратная матрица Для получения решения системы линейных уравнений надо набрать перечисленные ниже операторы. Записанные в выражении подряд три точки – признак переноса части этого выражения на следующую строку.
Решение 1 -->A=[2 3 7 6;... // матрица коэффициентов системы уравнений --> 3 5 3 1;... --> 5 3 1 3;... --> 3 3 1 6] A = 2. 3. 7. 6. 3. 5. 3. 1. 5. 3. 1. 3. 3. 3. 1. 6. -->B=[1; 3; 4; 5] // вектор-столбец правых частей системы уравнений B = 1. 3. 4. 5. ->A1=inv(A) // вычисление обратной матрицы A1 = 0.0285714 - 0.1285714 0.3857143 - 0.2 - 0.1238095 0.3071429 - 0.2547619 0.2 0.1714286 - 0.0214286 0.0642857 - 0.2 0.0190476 - 0.0857143 - 0.0761905 0.2 -->X=A1*B // Решение
X = 0.1857143 0.7785714 - 0.6357143 0.4571429
Другой способ решения системы уравнений – использование левого деления X=A\B Решение 2 -->A=[2 3 7 6; 3 5 3 1; 5 3 1 3; 3 3 1 6]; -->B=[1; 3; 4; 5]; -->X=A\B X = 0.1857143 0.7785714 - 0.6357143 0.4571429 Определение корней полинома Полиномом называется многочлен:
Для создания полинома следует перечислить в квадратных скобках все его коэффициенты (по возрастанию степени х), например, y=[1 2 3] Затем следует вызвать функцию poly(y,’x’,’c’). Здесь параметр ‘с’ означает, что полином строится по заданным его коэффициентам. Пример. -->y=[1 2 3]; -->P=poly(y,'x','c') P = 1 + 2x + 3x Для вычисления корней полинома используется функция roots(P) Здесь P - определенный с помощью функции poly полином. Вычисляются как действительные, так и комплексные корни полинома.
Пример 1.12. Вычислить корни полинома -->P=poly([-1 0.6 0.4 1],'x','c') P = 2 3 - 1 + 0.6x + 0.4x + x -->roots(P) ans = 0.7153636 - 0.5576818 + 1.0425361i - 0.5576818 - 1.0425361i Пример 1.13. Найти все корни уравнения -->Y=poly([0.139104 -0.7044 -0.01 1],'x','c') Y = 2 3 0.139104 - 0.7044x - 0.01x + x -->Korny=roots(Y) Korny = 0.21 0.72 - 0.92
|
||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 623; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.9.183 (0.006 с.) |

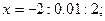
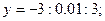
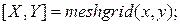
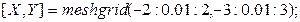
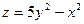 с помощью функции surf(x,y,z)
с помощью функции surf(x,y,z)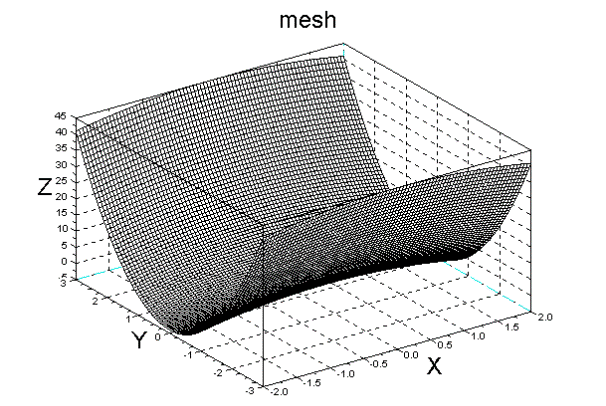
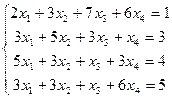
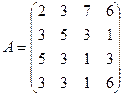
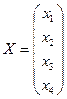
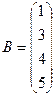
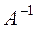 правую и левую части равенства (*). Получим:
правую и левую части равенства (*). Получим: 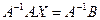 . Учитывая, что
. Учитывая, что 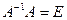 , где
, где  E – единичная матрица, найдем
E – единичная матрица, найдем