Кільце Ньютона. Інтерференція в природі.

Відповідь в посібнику ст. 88 де 2 пит. до ст. 89 „хвильові властивості світла, спостерігається в явищі дефракції.”

 

 

Хвильова і геометрична оптика

 

1. Тонка лінза.
2. Збиральна і розсіювальна лінза.
3. Побудова зображень у лінзі.
4. Формула тонкої лінзи.

 

Тонка лінза.

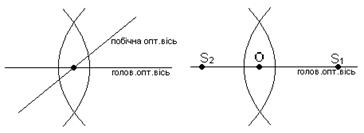
Прозоре тіло обмежене двома сферичними поверхнями називають лінзою (одна з поверхонь може бути плоска). Пряму, яка проходить через центр сферичних поверхонь називають головною оптичною віссю лінзи. На головній оптичній осі всередині кожної лінзи є т.О, яка називається оптичним центром лінзи. Будь-яка пряма яка проходить через оптичний центр лінзи т.О і не співпадає з головною оптичною віссю називається побічною оптичною віссю. Будь-який промінь, що проходить через оптичний центр лінзи т.О не заломлюється.

– збільшувальні лінзи

 

 

– розсіювальні лінзи

 

Лінзи середина яких тонша ніж краї називаються вгнутими (розсіювальні). Лінзи середина яких товстіша ніж краї називаються опуклими (збиральними). Якщо після виходу з лінзи промені сходяться то вони утворюють дійсне зображення. Коли ж промені, що пройшли через лінзу розходяться то перетинаються в одній точці не самі промені, а тільки їх продовження і зображення його будуть уявні. Спостерігати їх можна в оптичних приладах. Наприклад через лупу.

 

Збиральна і розсіювальна лінзи.

 

Збиральна лінза

 

мал.1

 

 

Якщо на збиральну лінзу спрямувати пучок променів, які паралельні її головній оптичній осі то ці промені зберуться в точці F з другого боку лінзи (мал..1). Ця точка F називається головним фокусом лінзи. У лінзі є два головних фокуси.

 

 

мал.2

 

Якщо в т.F розмістити джерело світла то після заломлення в лінзі промені підуть паралельно до головної оптичної осі лінзи (мал.2). Отже хід променів у лінзі взаємно оборотний

 

мал.3

 

 

Площина яка перпендикулярна до головної оптичної осі і яка проходить через т.F називається фокальною площиною (мал.3). Промінь, що проходить через оптичний центр лінзи т.О не заломлюється.

 

 

мал.4

 

Якщо промені падають на лінзу паралельно її побічній осі, наприклад АО (мал.4), то після заломлення в лінзі вони збираються на цій самій осі в т.В, яку називають побічним фокусом лінзи. Точка В утворена при перетині фокальної площини променем АО, який проходить через оптичний центр лінзи не заломлюючись.

Якщо в т.В розмістити джерело світла то після заломлення в лінзі промені підуть паралельно до побічної оптичної осі (мал. 4, тільки стрілочки на променях в другу сторону).

Розсіювальна лінза

 

 

Якщо на розсіювальну лінзу спрямувати пучок променів, які паралельні її головній оптичній осі то після лінзи ці промені йдуть розбіжним пучком, але так, що їх продовження збігаються в одній точці F, тобто в головному фокусі лінзи.

 

Побудова зображень у лінзі.

 

 

мал.1

 

Щоб побудувати зображення з допомогою збиральної лінзи користуються трьома променями.

І промінь паралельний головній оптичній осі заломившись проходить через її фокус.

ІІ її промінь проходить через головний оптичний центр лінзи без заломлення.

ІІІ промінь проходить через фокус лінзи і після заломлення в лінзі він пройде паралельно її головній оптичній осі.

Побудуймо зображення предмета АВ. Щоб знайти зображення т.А спрямуймо промінь АС паралельно її головній оптичній осі. Після заломлення він пройде через головний центр лінзи т.О без заломлення. У точці перетину цих двох променів і буде зображення А₁ т.А. І так можна побудувати інші точки предмета.

 

 

Якщо предмет знаходиться між головним фокусом лінзи і лінзою, то одержимо уявне зображення (мал. 2).

4. – формула для тонкої лінзи

d – відстань від предмета до лінзи (відстань ВО на малюнку).

f – відстань від лінзи до зображення (тобто відстань В₁О).

F– це фокусна відстань лінзи (ОF).

У формулі лінзи перед доданками , знаки потрібно ставити за таким правилом:

1. Якщо лінза збиральна то її фокус дійсний і перед доданком потрібно ставити "+". Коли ж лінза розсіювальна перед потрібно ставити знак "–".

2. Перед доданком ставлять знак "+", якщо зображення дійсне і "–", якщо зображення уявне.

Збільшення лінзи.

Н – висота зображення, h – висота предмета

– оптична сила лінзи

[D]= = д.п.т.р.

 

Сьома самостійна робота

 

 

Хвильова оптика.

 

1.Дефракція механічних хвиль.

2.Дефракція світла.

3.Дефракційна решітка.

4.Поляризація механічних хвиль.

5.Поляризація світла.

 

Дефракція механічних хвиль.

Дефракція від перешкоди.

Дифракцією називають огинання хвилями перешкод. Перешкоди порушують прямолінійність поширення хвиль. Явище дифракції для хвиль, які поширюються на поверхні води наведено на мал. 1-6. Якщо перешкода велика (порівняно з довжиною хвилі), то хвилі заходять за її краї (мал. 2), а дуже малу перешкоду хвилі огинають так, що за нею фронт хвилі ніяк не змінюються (мал. 1).

Дифракція від щілини:

Якщо щілина велика (порівняно з довжиною хвилі), то хвилі майже не заходять за її краї (мал.6). Якщо отвір маленький, хвилі помітно заходять за краї отвору (мал. 5). Якщо щілина дуже мала, то хвилі повністю покривають всю поверхню за перешкодою. У цьому разі отвір є ніби самостійним джерелом хвилі (мал.4).

 

Дефракція світла.

Дифракцією світла можна спостерігати тільки на значній відстані від перешкоди або отвору і розміри перешкоди повинні бути дуже малими, тому що довжина світлових хвиль дуже мала (менших від 1 мм в 1000 разів).

Нехай на шляху променю які йдуть від точкового джерела монохроматичного світла S розміщений дуже маленький непрозорий диск діаметром АВ (в області тіні) у вигляді темних і світлих тілець, які чередуються. В центрі екрану т.О буде світла точка, тому що різниця хвильових шляхів для цієї точки дорівнює нулю.

 

Дефракційна решітка.

Велику кількість паралельних і дуже близько розміщених вузьких щілин, які пропускають або відбивають світло називають дифракційною решіткою. Решітку виготовляють або з прозорої твердої речовини (скла) або з дзеркала, штрихи наносять алмазним різцем. Відстань від початкової 1-ї щілини до початкової 2-ї називають дифракційною сталою (d) або періодом решітки.

Нехай на решітку падає пучок паралельних монохроматичних променів, перпендикулярних до площини решітки, тоді дифракція призведе до поширення світлових хвиль з другого боку решітки від кожної щілини у всіх напрямках. Кожна щілина стає вторинним джерелом світла. (ніби в кожній щілині є маленька лампочка). На екрані світлові промені, які йдуть від різних щілин, накладаються (інтерферують). Якщо промені накладаються з однаковими фазами, то спостерігається підсилення світла – світла лінія, а якщо з протилежними фазами – послаблення світла – темна лінія. Якщо відкрита тільки одна щілина решітки, а всі інші закриті, то весь екран буде освітлений (дуже слабко).

Якщо на решітку падає пучок променів одного кольору (монохроматичних), то проти центра решітки на екрані буде видно максимум нульового порядку, а з обох боків від нього на однакових відстанях видно максимум першого порядку k=1, потім максимум другого порядку і т.д. Якщо дифракційну решітку освітлювати білим світлом, то в центрі екрану утвориться біла смуга (максимум нульового порядку), а з обох боків від неї спектри першого порядку, другого порядку і т.д.

d sin

- формула для дифракційної решітки.

- порядок спектру або порядок максимуму.

d – період решітки.

- кут під яким ми бачимо - тий порядок спектру ( = 1 – 1-й порядок і т. д.).

Виведення цієї формули в підручнику 11 кл. на ст. 141 (тільки виведення).