Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ввод изменений условий задачиСодержание книги
Поиск на нашем сайте
1. Перейдите на исходную таблицу (Таблица 2) 2. Как мы делали ранее, вызовите диалоговое окно Поиск решения 3. Измените граничные условия для Прод1: – В окне ограничения курсор на строку $В$3>=$В$4 – Изменить. На экране: диалоговое окно Изменить ограничение – Введите изменение: $В$3=10 – Ок 4. Аналогично ввести значение для Прод3: D3=6 5. Введите дополнительные условия для Прод2: – Добавить – Введите:С3=5 – Ок
Рис.12. Решение измененной задачи
6. Решите задачу, как мы это делали раньше. На экране: диалоговое окно, сообщающее о том, что поиск не может найти подходящего решения. Появление этого окна – признак несовместного решения. Чтобы решить подобную задачу, рассмотрим ее математическую модель:
Введем дополнительные необходимые ресурсы ti и запишем систему в виде:
Такая постановка задачи дает возможность определить минимальное значение дополнительных необходимых ресурсов t1, t2, t3. Математическая модель задачи примет вид:
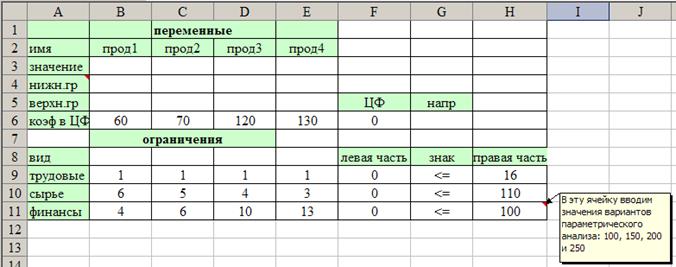
Преодоление несовместимости 1. Чтобы ввести систему (4), скопируйте таблицу для ввода данных (рис. 4) на отдельный лист книги Excel и отредактируйте так, как показано на рис.13 (данные) и рис.14 (формулы). Рис.13 отличается от рис. 4 следующим: – Введены столбцы F:H для переменных t1, t2, t3 – В ячейках F9:H11 введены –1 – В ячейке I6 зависимость для прибыли сохранена – В ячейку I4 введена зависимость для новой ЦФ, которая минимизируется
Рис.13. Форма ввода данных
Рис.14. Форма ввода данных в режиме представления формул
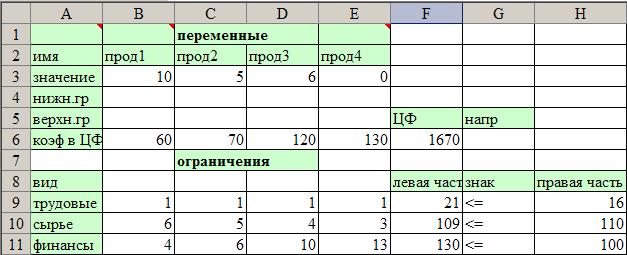
2. Сервис, Поиск решения… 3. Установите целевую ячейку I4 равной минимальному значению 4. В окно Изменяя ячейки введите В3:Н3 5. В окно Ограничения введите ограничения и граничные условия: В3=10, С3=5, D3=6, H3≥0, E3≥0, F3≥0, G3≥0, I9≤K9, I10≤K10, I11≤K11 6. Выполнить… На экране: результат решения (рис.15)
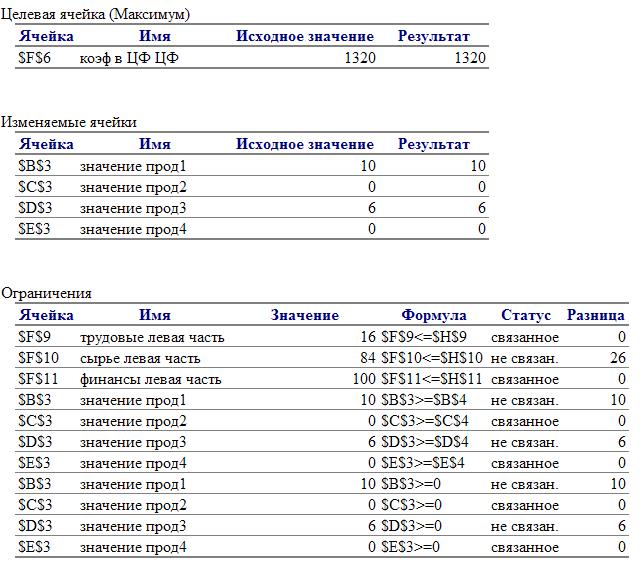
Рис.15. Оптимальное решение преодоления несовместности Из этого рисунка видно, что искомый дополнительный потребный ресурс равен t1=5, t2=0, t3=30. Это значит, что для заданного выпуска продукции необходимо иметь следующее количество ресурсов: трудовые 16+5=21, сырье 110+0=110, финансы 100+30=130. При этом будет получена прибыль, равная 1670. Анализ задач линейного программирования в Excel Анализ оптимального решения выполняется на основании применения положений симплекс-метода и начинается после успешного решения задачи, когда на экране появляется диалоговое окно Результат поиска решения. Решение найдено. С помощью этого окна можно вызвать отчеты трех типов: результаты, устойчивость, пределы. Отчет по результатам 1. Установите курсор на тип вызываемого отчета. Начнем с отчета по результатам 2. Ок. На экране: вызванный отчет на новом листе, на ярлычке которого указано название отчета. 3. Укажите курсором мыши на ярлычок с названием отчета. На экране: вызванный отчет (рис. 16).
Рис.16. Отчёт по результатам
Отчет по результатам состоит из трех таблиц: – Таблица 1 приводит сведения о ЦФ. В столбце Исходноприведены значения ЦФ до начала вычислений. – Таблица 2 приводит значения искомых переменных, полученных в результате решения задачи. – Таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий. В графе Формулаприведены зависимости, которые были введены в диалоговое окно Поиск решения. В графе Значениеприведены величины использованного ресурса. В графе Разницапоказано количество неиспользованного ресурса. Если ресурс используется полностью, то в графе Состояние указывается связанное, а при неполном использовании ресурса в этой графе указывается, не связан. Для Граничных условийприводятся аналогичные величины – разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием. 4. Отредактируйте отчет по результатам следующим образом (добавив примечания):
Рис. 17 Отредактированный Отчет по результатам
Рис. 18 Примечания в столбцах «Значение» и «Разница» Отчета по результатам Отчет по устойчивости Отчет по устойчивости состоит из двух таблиц (рис.19)
Рис.19. Отчёт по устойчивости В таблице 1 приводятся следующие значения для переменных: – результаты решения задачи – нормированную (редуцированную) стоимость, т.е. дополнительные двойственные переменные vj, которые показывают, насколько изменяется целевая функция при принудительном включении единицы этой продукции в оптимальное решение – коэффициенты целевой функции – предельные значения приращения коэффициентов целевой функции, при которых сохраняется набор переменных, входящих в оптимальное решение В таблице 2 приводятся аналогичные значения для ограничений: – величина использованных ресурсов – теневая цена, т.е. двойственные оценки, которые показывают, как изменится целевая функция при изменении ресурсов на единицу – значения приращения ресурсов,при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение. 5. Отредактируйте отчет по устойчивости следующим образом (добавив примечания):
Рис.20. Отредактированный Отчёт по устойчивости
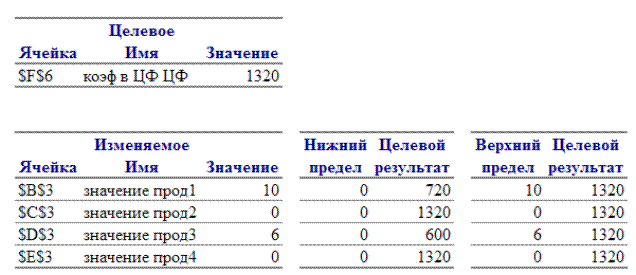
Рис.21. Примечания в столбце «Допустимое Увеличение» обоих таблиц Отчёта по устойчивости Отчет по пределам В этом отчете показано, в каких пределах может изменяться выпуск продукции, вошедший в оптимальное решение, при сохранении структуры оптимального решения: – приводятся значения xj в оптимальном решении – приводятся нижние пределы изменения значений xj – приводятся значения целевой функции при выпуске данного типа продукции на нижнем пределе.
Рис.22. Отчет по пределам Отредактируйте отчет по пределам следующим образом (добавив примечания):
Рис.23. Отредактированный Отчет по пределам
Рис.24. Примечания для столбцов «Нижний предел» и «Верхний предел» Отчета по пределам Параметрический анализ Под параметрическим анализом будем понимать решение задачи оптимизации при различных значениях того параметра, который ограничивает улучшение целевой функции. Вод данных Параметрический анализ будем выполнять для задачи, которая приведена в Таблице 2, решая ее при различных значениях имеющихся финансов. Для этого: 1. Составьте таблицу вариантов на отдельном листе (рис.25)
Рис.25. Таблица вариантов
2. Откройте таблицу с результатом решения задачи (рис.4) 3. Удалите результат решения, находящийся в В3:Е3:
Рис.26. Результат ввода данных
4. Решение задачи для первого варианта. 4.1. Введите в ячейку Н11=100 4.2. Сервис, Поиск Решения… 4.3. Выполнить. На экране: диалоговое окно Результаты поиска решения (рис.10) 4.4. Сохранить сценарий… На экране: диалоговое окно Сохранение сценария 4.5. Введите имя сценария финансы=100 4.6. Ок. На экране: диалоговое окно Результаты поиска решения (рис.10) 4.7. Ок. На экране: результат решения задачи для данного варианта финансы=100 (рис.11) 5. Решение задачи для последующих вариантов 5.1. Ввести в Н11 значения финансов из рис.15 для следующего варианта 5.2. Выполнить п. 4.2–п.4.7, при этом в п. 2.5 вводить имя сценария, соответствующее значению финансов.
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.123.103 (0.006 с.) |

 (2)
(2) (3)
(3)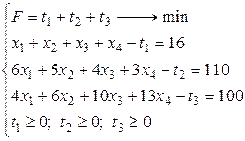 (4)
(4)