Экономико-математическая модель по оптимизации маршрута движения транспортных средств

Экономические задачи, связанные с нахождением наилучшей последовательности действий для достижения цели, удобно представлять для восприятия и анализа в виде графов. Граф - совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества пар вершин, которые называются ребрами.

Под сетевой моделью (сетевым графиком) понимается ориентированный граф, вершины которого отображают состояния (характеристики) некоторого объекта (например, строительного объекта, дорожной сети и т.д.), а дуги ‑ работы (процессы), связанные с этим объектом. Каждой дуге соответствует показатель (время, расстояние и т.д.), характеризующий работу (процесс).

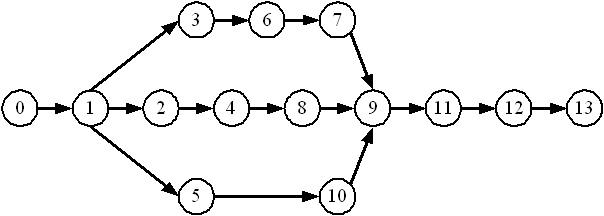
Рисунок 30. Пример ориентированного сетевого графика

Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.

В зависимости от задач управления применяют различные типы сетевых моделей, отличающиеся составом информации о комплексе работ (процессов). Среди них можно выделить два основных типа: модели с учетом только временных характеристик (ограничения на ресурсы не накладываются) и модели с учетом временных и ресурсных характеристик.

Модели первого типа не являются оптимизационными. Их применение позволяет найти минимальное время, в течение которого может быть выполнен весь комплекс работ, и определить календарные сроки начала и окончания каждой работы.

Модели второго типа относятся к задачам распределения ресурсов. Эти задачи являются оптимизационными и встречаются в разных постановках. В зависимости от принятого критерия оптимальности и характера ограничений их можно разбить на две основные группы:

задачи минимизации сроков наступления завершающего события при соблюдении заданных ограничений на использование ресурсов;

задачи оптимизации некоторого показателя качества использования ресурсов при заданных сроках выполнения комплекса. К этой группе относится, в частности, задача минимизации ресурсов при заданном времени выполнения комплекса работ.

Частным случаем сетевых моделей являются модели определения оптимального маршрута при различных условиях его формирования.

Постановка задачи и подготовка входной информации

Необходимо найти наиболее короткий маршрут доставки продукции из сельскохозяйственного предприятия (Пункт 1) на перерабатывающее (Пункт 15). Пунктами 2‑14 отмечены все развилки и перекрестки дорог.

Расстояния между пунктами известны и представлены в виде матрицы в таблице 35 (С_i-j, где i – номер пункта отправления, а j – номер пункта прибытия).

 

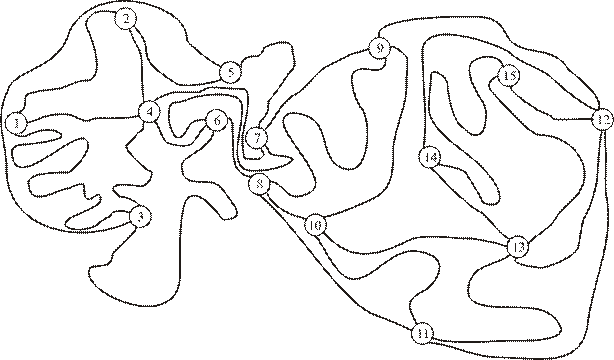
Рисунок 31. Карта автодорожной сети

Таблица 20. Расстояния между пунктами дорожной сети, км