Практикум по информационному обеспечению принятия управленческих решений

3.1. Применение MS EXCEL для решения задач линейного
программирования

Пример решения задачи по оптимизации использования ресурсов

Сельскохозяйственное предприятие специализируется на производстве зерна, сахарной свеклы и подсолнечника. Для возделывания этих сельскохозяйственных культур может быть выделено до 3 200 га пашни, дизельного топлива в объеме до 200 000 кг и минеральных удобрений в объеме до 400 000 кг действующего вещества. Требуется найти такое сочетание посевных площадей, которое обеспечило бы получение максимума прибыли.

Следует также учесть, что:

· площадь посева технических культур (сахарной свеклы и подсолнечника) не должна превышать 20% общей площади пашни;

· предприятием заключен договор на продажу зерна в объеме 105 000 ц.

Входная информация, необходимая для разработки экономико-математической модели приведена в таблице 1.

Таблица 1. Входная информация для разработки экономико-математической модели

Показатели	Сельскохозяйственные культуры
зерновые	сахарная свекла	подсолнечник
Урожайность, ц/га
Цена реализации 1 ц продукции, руб./ц
Выход товарной продукции с 1 га, тыс. руб.	19,2	57,0	20,4
Затраты на 1 га: материально-денежных средств, тыс. руб.	9,8	42,5	10,1
дизельного топлива, кг
минеральных удобрений, кг д. в-ва	90,0	360,0
Прибыль с 1 га, руб.	9,4	14,5	10,3

За неизвестные примем площади посева сельскохозяйственных культур по видам:

X₁ - зерновых культур;

X₂ - сахарной свеклы;

X₃ – подсолнечника.

Для построения экономико-математической модели задачи необходимо учесть все условия. В данном случае по этим условиям можно составить пять ограничений:

- сумма площадей посева сельскохозяйственных культур не должна превышать площади, имеющейся в предприятии (3 200 га). Коэффициенты при неизвестных характеризуют расход пашни на возделывание 1 га соответствующей сельскохозяйственной культуры. В правой части ограничения указывается объем площади пашни

1) Х₁+Х₂+Х₃<=3 200;

- сумма площадей посева технических культур не должна превышать площади, которая может быть отведена для этой цели (3200·20%=640 га). Коэффициенты при неизвестных характеризуют расход пашни, отводимой под технические культуры, на возделывание 1 га соответствующей технической культуры. В правой части ограничения указывается объем площади пашни, которая может быть отведена под технические культуры.

2) Х₂+Х₃<=640;

- третье и четвертое ограничения гарантируют, что использование ресурсов не превысит их наличия. То есть сумма произведений затрат ресурсов на 1 га на площади посева соответствующих сельскохозяйственных культур не должна превышать объемов ресурсов, имеющихся в предприятии. Коэффициенты при неизвестных характеризуют расход соответствующего ресурса на возделывание 1 га соответствующей сельскохозяйственной культуры. В правой части ограничений указывается наличие этих ресурсов в хозяйстве:

3) 50Х₁+ 124Х₂+68Х₃<=200 000;

4) 90Х₁+360Х₂+120Х₃<=350 000;

- пятое ограничение гарантирует производство запланированного объема реализации зерна. В качестве коэффициентов при переменных выступает выход зерна с 1 га площади посева зерновых культур. В правой части указывается запланированный объем реализации зерна

5) 40Х₁>=105 000.

В результате получена система пяти линейных неравенств с тремя неизвестными. Требуется найти такие неотрицательные значения этих неизвестных Х₁>=0; Х₂>=0; Х₃>=0, которые бы удовлетворяли данной системе неравенств и обеспечивали получение максимума прибыли:

Z_max = 9,4Х₁+14,5Х₂+10,3Х₃.

В качестве коэффициентов при неизвестных в целевой функции выступает прибыль в расчете на 1 га посева сельскохозяйственных культур.

Поскольку данная задача решается с помощью MS Excel, то и подготовку всей входной информации для построения экономико-математической модели целесообразно осуществлять также с использованием этого табличного процессора. Эти расчеты представлены на листе «Исходные» файла MS Excel (рисунок 7). Это не только облегчает расчеты, связанные с подготовкой входной информации, но и дает возможность в дальнейшем автоматически обновлять параметры экономико-математической модели при реализации различных вариантов.

Экономико-математическая модель по оптимизации структуры посевных площадей в матричном виде заполняется на листе «Модель» файла MS Excel, уже содержащего лист «Исходные» (рисунок 8). Технико-экономические коэффициенты, оценки целевой функции (столбцы D, E, F), объемы ограничений (столбец I) рекомендуется определять через ссылки на соответствующие ячейки листа «Исходные».

Рисунок 7. Входная информация для разработки экономико-математической модели

 

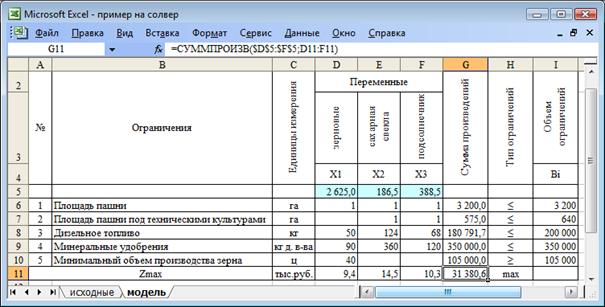
Рисунок 8. Экономико-математическая модель по оптимизации

структуры посевных площадей

На рисунке 8 показано, каким образом произошло заполнение ячейки F9, описывающей затраты минеральных удобрений на 1 га посева подсолнечника (смотри строку «f_x» рисунка 8).

В столбцы А (№), В (Ограничения), С (Единицы измерения) и H (Тип ограничений) вводятся соответствующие данные в текстовом формате. Они не используются в расчетах и служат для информативности и облегчения понимания содержания модели.

Для искомых величин переменных Х₁, Х₂, Х₃ необходимо оставить пустые ячейки соответственно D5, E5, F5. Столбец G (Сумма произведений), предназначен для определения суммы произведений значений искомых неизвестных (ячейки D5, E5, F5) и технико-экономических коэффициентов по соответствующим ограничениям (строки 6-10) и целевой функции (строка 11). Формула нахождения суммы произведений для строки с целевой функцией (для ячейки G11) приведена в верхней строке рисунка 9.

 

Рисунок 9. Экономико-математическая модель по оптимизации

структуры посевных площадей

То есть, в столбце G будет определяться:

· количество используемых ресурсов (ячейка G6 – общей площади пашни; G7 – пашни, которая может быть использована под посевы технических культур; G8 – трудовых ресурсов; G9 – минеральных удобрений);

· количество произведенного зерна (ячейка G10);

· величина прибыли (ячейка G11).

Таким образом, построен опорный план и получено первое допустимое решение. Значения неизвестных Х₁, Х₂, Х₃ равны нулю (ячейки D5, E5, F5 - пустые ячейки), ячейки столбца G «Сумма произведений» по всем ограничениям (строкам 6-10) и целевой строке (строка 11) также имеют нулевые значения.

Для оптимизации имеющегося плана воспользуемся инструментом Поиск решения, который находится в меню Сервис. Если нет такой команды в меню Сервис, необходимо в пункте Надстройка поставить галочку напротив Поиск решения. После этого данная процедура станет доступной в меню Сервис.

После выбора команды Поиск решения появится диалоговое окно.

Рисунок 10. Диалоговое окно команды Поиск решения

Поскольку в качестве критерия оптимизации нами выбрана максимизация прибыли, в поле Установить целевую ячейку необходимо ввести ссылку на ячейку, содержащую формулу расчета прибыли. В нашем случае это ячейка $G$11.

Рисунок 11. Диалоговое окно команды Поиск решения

Чтобы максимизировать значение конечной ячейки путем изменения значений влияющих ячеек (влияющими, в данном случае это и изменяемые ячейки, являются ячейки, которые предназначены для хранения значений искомых неизвестных), переключатель необходимо установить в положение Равной максимальному значению.

В поле Изменяя ячейки необходимо ввести ссылки на изменяемые ячейки, разделяя их запятыми, либо, если ячейки находятся рядом, указывая первую и последнюю ячейку, разделяя их двоеточием ($D$5:$F$5).

Рисунок 12. Диалоговое окно команды Поиск решения

В поле Ограничения необходимо ввести все ограничения, накладываемые на поиск решения.

В разделе Ограничения диалогового окна команды Поиск решения необходимо выбрать функцию Добавить. Появится следующее диалоговое окно.

Рисунок 13. Диалоговое окно команды Добавление ограничения

Добавление ограничений рассмотрим на примере всех ограничений. В поле Ссылка на ячейку необходимо ввести адрес одной ячейки (совокупности ячеек), на которую накладываются ограничения. В нашем случае это ячейки $G$6:$G$9, в которых находятся формулы расчета количества используемых ресурсов. Затем из раскрывающегося списка условных операторов необходимо выбрать необходимый знак, который должен располагаться между ссылкой на ячейку и ограничением. В нашем случае, это <=. В поле Ограничение необходимо ввести ссылки на ячейки, в которых находятся значения, характеризующие наличие ресурсов. В нашем случае это ячейки $I$6:$I$9.

В результате диалоговое окно примет следующий вид.

Рисунок 14. Диалоговое окно команды Добавление ограничения

После подтверждения добавления описанных ограничений (необходимо нажать кнопку Добавить), аналогично добавляется ограничение по обеспечению минимального объема производства зерна (строка 10).

Рисунок 15. Диалоговое окно команды Добавление ограничения

После описания последнего ограничения необходимо вернуться в диалоговое окно команды Поиск решения, нажав виртуальную кнопку OK.

Рисунок 16. Диалоговое окно команды Добавление ограничения

В случае внесения изменения в какое-либо из ограничений, необходимо выделить его в списке Ограничения и выбрать команду Изменить. Аналогичным способом можно удалить ненужное ограничение.

После добавления ограничений описываются параметры поиска решения. Для этого в диалоговом окне команды Поиск решения выбирается команда Параметры (рисунок 17).

Опция Линейная модель в диалоговом окне команды Параметры поиска решения служит для ускорения поиска решения линейной задачи оптимизации.

Опция Неотрицательные значения позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых она не была указана в поле Ограничение диалогового окна Добавить ограничение.

Остальные параметры можно оставить без изменений либо установить необходимые параметры, используя опцию Справка.

Выбор параметров подтверждается нажатием виртуальной кнопки ОК

Рисунок 17. Диалоговое окно команды Параметры поиска решения

Для запуска задачи на решение необходимо нажать виртуальную кнопку Выполнить диалогового окна команды Поиск решения.

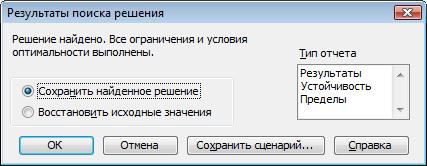
Рисунок 18. Диалоговое окно команды Результаты поиска решения

Для сохранения найденного решения на листе необходимо выбрать в диалоговом окне Результаты поиска решения опцию Сохранить найденное решение.

Для восстановления исходных данных применяется опция Восстановить исходные значения диалогового окна Результаты поиска решения.

Прерывание поиска решения осуществляется нажатием клавиши ESC.

В результате решения и сохранения результатов поиска модель примет вид, представленный на рисунке 19.

В ячейках D5:F5получены значения искомых неизвестных (площади посева равны: зерновых ‑ 2 625,0 га, сахарной свеклы – 186,5 га, подсолнечника – 388,5 га), в ячейках G6:G9 определены объемы используемых ресурсов (общей площади пашни – 3200 га; площади пашни, которая будет использоваться под посевы технических культур, – 575 га; дизельного топлива – 180 791,7 кг; минеральных удобрений – 350 000 кг д. в-ва), в ячейке G10 найдено количество зерна, которое может быть реализовано, ‑ 105 000 ц). При этом величина прибыли достигает 31 380,6 тыс. руб. (ячейка G11).

Рисунок 19. Экономико-математическая модель по оптимизации структуры посевных площадей с результатами решения

В случае если в результате поиска не было найдено решение, удовлетворяющее заданным условиям, в диалоговом окне Результаты поиска решения появится соответствующее сообщение

Рисунок 20. Диалоговое окно команды Результаты поиска решения

Одной из наиболее часто встречающихся причин невозможности найти оптимальное решение является невыполнение одного или нескольких ограничений. Сохранив найденное решение, требуется построчно сравнить полученные значения столбцов «Сумма произведений» и «Объем ограничений» и проверить, удовлетворяет ли отношение между ними ограничению, стоящему в столбце «Тип ограничений». Найдя, таким образом, невыполняемые ограничения, необходимо найти и ликвидировать причины, обусловливающие невозможность соблюдения данного конкретного условия (это может быть, например, слишком большие или, наоборот, очень маленькие запланированные объемы ограничений и т.п.).

Пример решения транспортной задачи

В агрохолдинге имеется четыре склада, на которых хранится 1 350 т дизельного топлива, которое необходимо доставить в пять механизированных отрядов. Общая потребность механизированных отрядов в дизельном топливе составляет 1 300 т.

Информация о наличии дизельного топлива в разрезе складов и потребность в дизельном топливе в разрезе механизированных отрядов приведены в таблице 2.

Таблица 2. Информация о наличии и потребности в дизельном топливе, т

Склады	Имеется дизельного топлива		Механизированные отряды	Требуется дизельного топлива
Склад №1			Мехотряд №1
Склад №2			Мехотряд №2
Склад №3			Мехотряд №3
Склад №4			Мехотряд №4
			Мехотряд №5
Всего имеется	1 350		Всего требуется	1 300

Требуется определить, с какого склада, сколько и в какой механизированный отряд поставлять дизельное топливо, чтобы объем грузооборота был минимальным.

Информация о расстояниях между складами и механизированными отрядами приведена в таблице 3.

Таблица 3. Информация о расстояниях между складами и

механизированными отрядами, км

Поставщики	Потребители
Мехотряд №1	Мехотряд №2	Мехотряд №3	Мехотряд №4	Мехотряд №5
Склад №1
Склад №2
Склад №3
Склад №4

На пересечении столбца конкретного механизированного отряда со строкой склада находится информация о расстояниях между этим пунктом доставки и складом. Например, расстояние между мехотрядом №1 и складом №3 равно 16 км.

Исходные данные для решения транспортной задачи представлены на листе «Транспортная задача» файла MS Excel (рисунок 21).

После формирования таблицы с исходными данными необходимо сформировать в матричной форме экономико-математическую модель транспортной задачи, которая представлена на рисунке 16.

Каждое значение в ячейках (диапазон ячеек C12:G15) на пересечении столбца конкретного пункта потребления и строки склада означает количество тонн, поставляемых с этого склада в данный пункт потребления. Поэтому в первом опорном плане эти ячейки заполняются нулями.

 

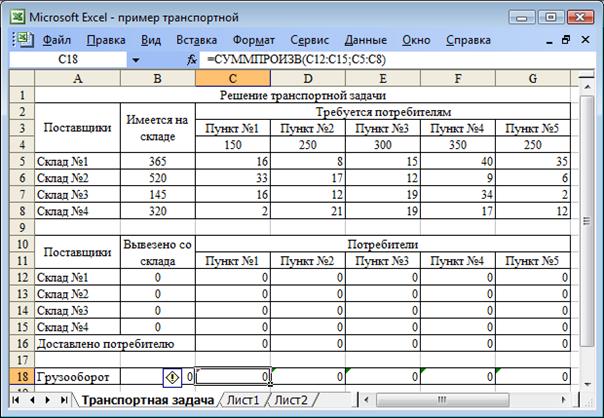
Рисунок 21. Исходные данные для решения транспортной задачи

Рисунок 22. Исходные данные для решения транспортной задачи

Ячейки B12:B15 (Вывезено со склада) определяются суммированием элементов соответствующих строк. Например, ячейка B12=СУММ(C12:G12).

Ячейки C16:G16 (Доставлено потребителю) определяются суммированием элементов соответствующих столбцов. Например, ячейка C16СУММ(C12:C15).

В 18-ой строке в ячейках C18:G18 определим грузооборот по каждому пункту потребления. Грузооборот определяется как сумма произведений расстояний от конкретного пункта потребления до каждого из складов и объемов перевозок груза в этот пункт потребления с каждого склада. Пример формулы расчета ячейки С18 приведен в строке fx на рисунке 22.

В ячейке В18 по формуле СУММ(С16:G16) будет вычисляться общий объем грузооборота дизельного топлива. В первом опорном плане все объемы грузоперевозок равны нулю.

Для решения транспортной задачи воспользуемся процедурой Поиск решения, которая находится в меню Сервис.

После выбора данной процедуры появится диалоговое окно команды Поиск решения (рис.23).

Рисунок 23. Диалоговое окно команды Поиск решения

Поскольку в качестве критерия оптимальности выбрана минимизация грузооборота, в поле Установить целевую ячейку: необходимо ввести ссылку на ячейку, содержащую формулу расчета общего объема грузооборота дизельного топлива. В нашем случае это ячейка $B$18.

Чтобы минимизировать значение конечной ячейки путем изменения значений влияющих ячеек (влияющими, в данном случае это и изменяемые ячейки, являются ячейки, которые предназначены для хранения значений искомых неизвестных), переключатель установите в положение минимальному значению.

В поле Изменяя ячейки: необходимо ввести ссылки на изменяемые ячейки, разделяя их запятыми; либо, если ячейки находятся рядом, указывая первую и последнюю ячейку, разделяя их двоеточием ($С$12:$G$15). Это означает, что для достижения минимального грузооборота перевозок будут меняться значения в ячейках с С12 по G15, то есть будет изменяться количество груза, перевезенного по конкретному маршруту (рис. 24).

Рисунок 24. Диалоговое окно команды Поиск решения

В поле Ограничения: необходимо ввести все ограничения, накладываемые на поиск решения.

В разделе Ограничения: диалогового окна команды Поиск решения необходимо выбрать функцию Добавить. Появится следующее диалоговое окно (рис.25).

Рисунок 25. Диалоговое окно команды Добавление ограничения

Экономический смысл ограничений в данной задаче состоит в следующем:

· с каждого склада должно быть вывезено дизельного топлива не больше, чем на нем есть;

· потребности каждого потребителя должны быть удовлетворены полностью;

· объем грузоперевозок не может быть отрицательным.

То есть:

B12≤B5, B13≤B6, B14≤B7, B15≤B8 или $B$12:$B$15<=$B$5:$B$8;

C16=C4, D16=D4, E16=E4, F16=F4, G16=G4 или $C$16:$G$16=$C$4:$G$4

После ввода первого ограничения следует нажать кнопку Добавить и ввести второе ограничение. По окончании его ввода необходимо нажать на виртуальную кнопку ОК.

После выполнения вышеперечисленных инструкций диалоговое окно команды Поиск решения будет иметь следующий вид (рис. 26).

Рисунок 26. Диалоговое окно команды Поиск решения с заполненными полями

Обратите внимание, условие неотрицательности переменных в системе ограничений не описывается. Это условие будет задано при описании параметров решения данной задачи.

В случае внесения изменения в какое-либо из ограничений, необходимо указать его в списке Ограничения диалогового окна команды Поиск решения и выбрать команду Изменить. Аналогичным способом можно удалить ненужное ограничение. После добавления ограничений описываются параметры поиска решения. Для этого в диалоговом окне команды Поиск решения выбирается команда Параметры. Диалоговое окно команды Параметры поиска решения приведено на рисунке 27.

Опция Линейная модель в диалоговом окне команды Параметры поиска решения служит для ускорения поиска решения линейной задачи оптимизации.

Рисунок 27. Диалоговое окно команды Параметры поиска решения с заполненными полями

Опция Неотрицательные значения позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых она не была указана в поле Ограничение диалогового окна Добавить ограничение. Остальные параметры можно оставить без изменений, либо установить необходимые параметры, используя опцию Справка. Выбор параметров поиска подтверждается нажатием виртуальной кнопки ОК.

Для запуска задачи на решение необходимо нажать виртуальную кнопку Выполнить диалогового окна команды Поиск решения.

Рисунок 28. Диалоговое окно команды Результаты поиска решения

Для сохранения найденного решения на листе, необходимо выбрать в диалоговом окне Результаты поиска решения опцию Сохранить найденное решение (рис. 28). Для восстановления исходные данные, необходимо выбрать в диалоговом окне Результаты поиска решения опцию Восстановить исходные значения.

Прерывание поиска решения осуществляется нажатием клавиши ESC.

В результате решения и сохранения результатов поиска решения модель примет вид, представленный на рисунке 29.

Рисунок 29. Результаты поиска решения

В результате решения потребность всех механизированных отрядов удовлетворена полностью. Потребность в дизельном топливе механизированного отряда №1 (150 т) удовлетворяется полностью за счет запасов, имеющихся на складе №4. С этого же склада 170 т дизельного топлива доставляется в мехотряд №5. Еще 80 т, необходимые данному мехотряду, будут доставлены со склада №3.

Со склада №3 15 т дизельного топлива будут доставлены в мехотряд №2. Остальная потребность этого мехотряда (235 т) будет покрыта за счет дизельного топлива, хранящегося на складе №1. Потребность в дизельном топливе мехотряда №3 будет покрыта со склада №1 (13 т) и склада №2 (170 т). Вся потребность мехотряда №3 будет покрыта за счет доставки дизельного топлива со склада №2.

Со склада №3 остались невывезенными 50 т дизельного топлива.

Суммарный объем грузоперевозок составил 9 500 тонно-километров.

Задание для самостоятельной работы

Вопросы для самоконтроля

3.2. Решение задач оптимального выбора методами линейного
программирования