
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение экономико-математической модели.Содержание книги
Поиск на нашем сайте
Система переменных данной экономико-математической задачи представлена основными и вспомогательной переменными. За основные переменные ( Все условия задачи записаны в виде линейных уравнений и неравенств (ограничений), которые можно разбить на группы: · по гарантированному удовлетворению потребности сельскохозяйственных животных в питательных веществах, макро- и микроэлементах; · по пределам включения отдельных кормов или групп кормов в рацион; · по соотношению отдельных видов кормов и добавок; · по определению суммарного количества кормовых единиц в рационе. Основными ограничениями (с 1 по 15) являются условия по гарантированному удовлетворению потребности сельскохозяйственных животных в питательных веществах, макро- и микроэлементах
где
Эти ограничения составляются на основании данных о содержании питательных веществ, макро- и микроэлементов в 1 кг кормов и кормовых добавок (таблица 5) и их минимальном содержании в суточном рационе кормления. Например, ограничение, гарантирующее, что в суточном рационе кормления будет содержаться не менее 5,3 к.ед., будет записано в следующем виде: 1,20X1+1,15X2+1,18X3+1,00X4+0,72X5+0,48X6+0,20X7+0,32X8+0,20X9+1,12X10+0,76X11+0,50X12>=5,5. Коэффициент 1,20 при X1 обозначает, что в одном килограмме дробленой пшеницы содержится 1,20 к.ед., коэффициент 0,48 при X6 ‑ что в одном килограмме сена содержится 0,72 к.ед. и т.д. Дополнительные ограничения (по пределам включения отдельных кормов или групп кормов в рацион и по соотношению отдельных видов кормов и добавок) разделены на три группы. Пределы включения отдельных кормов или групп кормов в рацион могут описываться двумя способами: во-первых, через указание минимальных и максимальных границ скармливания отдельных кормов и их групп в процентах от суммарного количества кормовых единиц, содержащихся в рационе; во–вторых, через ограничение максимального суточного потребления отдельных кормов в физической массе.
Первую группу дополнительных ограничений (с 16 по 25) составляют ограничения по установлению минимальных и максимальных границ скармливания отдельных кормов и их групп в процентах от суммарного количества кормовых единиц, содержащихся в рационе
где
αh13, βh13 - нижняя и верхняя граница включения в рацион h-ой группы корма в процентах. Например, условие по минимальному (20%) и максимальному (30%) удельному весу концентрированных кормов в рационе имеет вид: нижняя граница 1,20X1+1,15X2+1,18X3+1,00X4>=0,20X13 или 1,20X1+1,15X2+1,18X3+1,00X4 - 0,20X13>=0; верхняя граница 1,20X1+1,15X2+1,18X3+1,00X4<=0,30X13 или 1,20X1+1,15X2+1,18X3+1,00X4 - 0,30X13<=0. Вторую группу дополнительных ограничений (с 26 по 28) составляют ограничения по максимальному суточному потреблению отдельных кормов в физической массе
где
Ограничения по максимальному суточному потреблению витаминно-травяной муки в размере 1,8 кг, силоса – 30 кг, патоки - 2,0 кг имеют следующий вид: X5 <= 1,8; X9 <=30,0; X11<= 2,0 Третью группу дополнительных ограничений (с 29 по 30) составляют ограничения по соотношению отдельных видов кормов и добавок
где
Эти ограничения формулируют с использованием алгебраических преобразований. Так, ограничение по включению комбикорма в размере не более 50 % от питательности концентрированных кормов первоначально имеет форму 1,00X4<=0,50·(1,20X1+1,15X2+1,18X3+1,00X4) Проведем преобразования: 1,00X4 - 0,50·(1,20X1+1,15X2+1,18X3+1,00X4) <=0, -0,50·1,20X1-0,50·1,15X2-0,50·1,18X3+ (1,00-0,50) ·X4<=0, 0,600X1-0,575X2-0,590X3+0,500X4<=0. Ограничение по включению сена в группу грубых кормов в размере не более 55% их питательности будет записано так: 0,48X6<=0,55·(0,48X6+0,20X7)
Проведем преобразования: 0,48X6 - 0,55·(0,48X6+0,20X7) <=0, (1‑0,55)·0,48X6‑0,55*0,20X7<=0, 0,216X6‑0,110X7<=0. Вспомогательное ограничение (31) накладывается для подсчета суммарного количества кормовых единиц в рационе
где aj - содержание кормовых единиц в единице j -го корма и кормовой добавки. Это ограничение имеет следующий вид: 1,20X1+1,15X2+1,18X3+1,00X4+0,72X5+0,48X6+0,20X7+0,32X8+0,20X9+1,12X10+0,76X11+0,5X12 = X13, или 1,20X1+1,15X2+1,18X3+1,00X4+0,72X5+0,48X6+0,20X7+0,32X8+0,20X9+1,12X10+0,76X11+0,5X12-X13= 0. Значения переменных должны быть неотрицательными:
В качестве критерия оптимальности данной задачи принята минимизация себестоимости рациона
где сj - себестоимость или цена приобретения 1 кг j -го корма или кормовой добавки/ Целевая функция записывается следующим образом: Zmin=2,41X1+2,03X2+4,27X3+2,24X4+2,64X5+0,79X6+0,25X7+0,83X8+0,53X9+0,41X10+1,50X11+5,48X12 Подготовленная информация сводится в экономико-математическую модель, которая в матричной форме представлена в таблице 7. Реализация разработанной экономико-математической модели по оптимизации рационов кормления осуществляется с помощью надстройки Поиск решения пункта меню Сервис Microsoft Excel. Порядок работы с данной надстройкой описан в разделе 3.1.1. настоящего учебного пособия.
|
||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.27.43 (0.01 с.) |

 ) принимается искомое количество кормов и кормовых добавок в суточном рационе кормления 1 головы скота; эти переменные измеряются в килограммах. Вспомогательная переменная
) принимается искомое количество кормов и кормовых добавок в суточном рационе кормления 1 головы скота; эти переменные измеряются в килограммах. Вспомогательная переменная  используется для определения суммарного содержания в рационе кормовых единиц.
используется для определения суммарного содержания в рационе кормовых единиц. ,
, - искомое количество кормов и кормовых добавок в суточном рационе кормления 1 головы скота;
- искомое количество кормов и кормовых добавок в суточном рационе кормления 1 головы скота; - содержание питательных веществ, макро- и микроэлементов i -го вида в 1 кг j -го вида корма или кормовой добавки;
- содержание питательных веществ, макро- и микроэлементов i -го вида в 1 кг j -го вида корма или кормовой добавки; - минимально допустимое количество питательных веществ i-го вида в рационе.
- минимально допустимое количество питательных веществ i-го вида в рационе.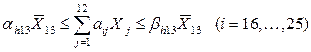 ,
, - суммарное содержание в рационе кормовых единиц;
- суммарное содержание в рационе кормовых единиц; ,
,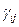 - булевы коэффициенты связи (равны либо 0, либо 1) по i -му виду корма;
- булевы коэффициенты связи (равны либо 0, либо 1) по i -му виду корма; - максимальное суточное потребление i -го корма в физической массе.
- максимальное суточное потребление i -го корма в физической массе. ,
, - вид корма, удельный вес которого в h-ой группе кормов ограничен;
- вид корма, удельный вес которого в h-ой группе кормов ограничен; - максимальный удельный вес j-го корма в h-ой группе кормов.
- максимальный удельный вес j-го корма в h-ой группе кормов. ,
, ,
,  .
.
 ,
,


