
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непротиворечивость системы аксиом Вейля 3-х мерного евклидового пространства.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
К любой системе аксиом пред след требования: непротиворечивость, независимость, полнота. Непротивор главное, т.к. все аксиомы получ далее должны удовл ему. Система аксиом называется непротиворечивой, если существует база, на которой можно задать рассматриваемую структуру рода Т. Чтобы доказать непротиворечивость системы аксиом, достаточно построить какую-либо интерпретацию этой системы аксиом. При построении интерпретации мы должны использовать «достаточно надежные» понятия, относительно которых у нас есть уверенность, что их система внутренне непротиворечива. Только в этом случае можно утверждать, что наша система аксиом А1,А2, …, Аn внутренне непротиворечива, и, значит, в теории Г(Т) мы не получим двух теорем, отрицающих одна другую, как бы далеко мы ни развивали эту теорию. Вопрос о внутренней непротиворечивости системы аксиом может быть решен только средствами математической логики. При построении интерпретаций систем аксиом, определяющих структуры, изучаемые в геометрии, мы используем различные числовые множества, считая «наиболее надежными» понятия, взятые из арифметики вещественных чисел. Поэтому при исследовании непротиворечивости системы аксиом А1,А2, …, Аn, не прибегая к средствам математической логики, мы в лучшем случае можем прийти к утверждению такого вида: система аксиом А1,А2, …, Аn непротиворечива, если непротиворечива арифметика вещественных чисел. Теорию действит.чисел будем считать непротиворечивой. Из объектов этой теории необходимо построить модель, т.е. основным отношениям придать конкретный смысл. Докажем сначала непротиворечивость 3-х мерного евклид.пр-ва (I-IV). Под вектором будем понимать упорядоченную тройку вещественных чисел, взятых в определ.порядке и заключенных в фигурную скобку( Точка – это упорядоченная тройка вещественных чисел, заключенных в круглую скобку(M(x1,x2,x3)). В скобках записана координата точки или вектора. Основные отношения: дано 1. 2. 3. 4. A(ai), B(bi), Пара AB и вектор
I1. ( I2 –вып-ся I3 : I4: III1:
Разложение векторов в базис однозначно => III2.
уравнений => имеет бесчисл.мн-во решений =>лин.завис. IV. IV1: IV2- вып-ся(ассоциат.закон) IV3 – вып-ся (по дистриб.закону) IV4:
V. 1-4–вып-ся V3. A(a1, a2, a3), (
V4. A(ai), B(bi), C(ci), i=1,2,3
След-но все 18 аксиом – справедливые теоремы теории действ-х чисел. Мы построили модель.
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 826; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.235.157 (0.007 с.) |

 {x1,x2,x3}).
{x1,x2,x3}). {x1,x2,x3},
{x1,x2,x3},  {y1,y2,y3}.
{y1,y2,y3}. +
+  = { x1+y1, x2+y2, x3+y3}
= { x1+y1, x2+y2, x3+y3} ={
={ 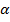 x1,
x1,  x3}
x3}
 = { x1
= { x1  y1+ x2
y1+ x2  =
=  -
-  ,
, 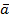 {a1,a2,a3},
{a1,a2,a3}, 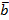 {b1,b2,b3},
{b1,b2,b3},  {c1,c2,c3}
{c1,c2,c3} ={
={  )
)  ;
;  )
)  ;
;  )
)  }= {
}= {  +(
+( +(
+(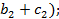
 +(
+( ) – выполняется.
) – выполняется. ,
, 
 ,
,  = {
= { 
 покажем, что векторы линейно зависимы,т.е.
покажем, что векторы линейно зависимы,т.е.
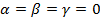 =>
=>  лин.независ.
лин.независ. {d1,d2,d3}
{d1,d2,d3}
 => число неизвестных больше числа
=> число неизвестных больше числа , {
, { 
 ={
={  => вып-ся
=> вып-ся => {
=> {  =>
=>  B) (
B) ( )
) {b1-a1, b2-a2, b3-a3} – вып-ся
{b1-a1, b2-a2, b3-a3} – вып-ся {c1-b1, c2-b2, c3-b3},
{c1-b1, c2-b2, c3-b3},  {c1-a1, c2-a2, c3-a3}
{c1-a1, c2-a2, c3-a3} {c1-a1, c2-a2, c3-a3}=
{c1-a1, c2-a2, c3-a3}= 


