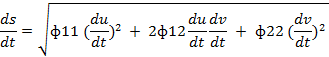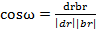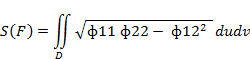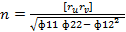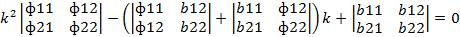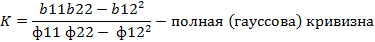Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равносоставленность многоугольниковСодержание книги
Поиск на нашем сайте
0:Два многоугольника будем называть равносоставленными, если их можно разрезать на одинаковое число соответственно равных многоугольников Или
Теорема: Всякий треугольник равносоставлен с прямоугольником, основание которого равно одной стороне треугольника, а высота равна половине одной из сторон соответствующей высоты треугольника Равновеликости многоугольников Понятие равновеликости явл обобщением понятия равносоставленности. 0: Два многоугольника будем называть равновеликими, если каждому из них можно добавить одинаковое число соответственно равных многоугольников так, что получатся равносильные многоугольники. Два равносоставленных многоугольника явл равновеликими. Теорема: Два треугольника, имеющие рывные основания и равные, соответствующие им высоты, равноелики. Теорема:Параллелограммы с равными основаниями и равными высотами равновелики Теорема: Если два многоугольника равносоставленны, то они равновеликими Теорема Бояи – Гервина Всякие два равновеликих многоугольника явл равносоставленными
Топологическое пространство. Топологическое многообразие. Эйлеровая характеристика двумерного многообразия. Теорема Эйлера для многогранников. Топологическое простраство Опр: Пусть Х-некоторое не пустое множество будет называть пространство-носитель и пусть 1) Объединение любой системы множеств из 2) Пересечение конечного числа множеств из 3) Пусть множество Множество Х вместе с заданной в нем топологией Элементы из Х называются точками. Множество Пример: 1) 2)
3) Каждое метрическое пространство является топологическим пространством. Многообразие Пусть (X, Если х k-мерным топологическим многообразием (или просто k-мерным многообразием) называют отделимое топологическое пространство (X, В топологии доказывают, что число k (размерность многообразия) является топологическим инвариантом, т. е. не меняется при любых гомеоморфизмах пространства Клеточное разложение. Обозначим через R+ множество тех точек из Rk(k = 1,2), у которых координата xk удовлетворяет условию xk Множество всех краевых точек называется краем многообразия (X, У). Назовем клеткой любое многообразие с краем, гомеоморфное выпуклому многоугольнику. При этом предполагается, что для данной клетки этот гомеоморфизм фиксирован. Образ вершины многоугольника при этом гомеоморфизме мы назовем вершиной клетки, а образ стороны многоугольника — стороной клетки. Мы скажем, что двумерное многообразие F разложено на конечное множество клеток F1, F 2, ..., Fn, если выполняются два условия: 1.эти клетки образуют покрытие многообразия F; 2.пересечение любых двух клеток Fi и Fj(i Пусть К — клеточное разложение двумерного многообразия. Точка х Число Топологическое многообразие. В топологических преобразованиях меняются многие свойства фигур (длина, площади, прямолинейность). Некоторые более сильные сохраняются. Теорема Эйлера: Если
Док-во: пусть многогранник внутри пустой. Пусть Одну грань вырежем останется поверхность ее растянем на плоскости. Число вершин и ребер не изменилось, а граней станет на 1 меньше.
Трианвумеруем (величина не меняется) диагоналями разбиваем на треугольники. 2 типа треугольника: 1. С границей одной стороной; 2) с границей 2 сторонами. Если отрежем треугольник 1-го типа, число граней уменьшится на 1, вершин на 1. Если 2-го типа – вершин и граней уменьшится на 1, ребер на 2. Теорема Эйлера позволяет установить если правильные многогранники. Существует 5 типов: Многогранник называется правильным если в гранях его лежит равные правильные многоугольники, а в вершине правильные n-гранные углы, m-угольники в гранях.
n-ребер.
1) 2) 3) 4) 5)
12. Линии и поверхности в Е3. Первая основная квадратичная форма поверхности и её приложения.
векторную функцию r(t) скалярного аргумента t, определенную в промежутке J. Эта функция имеет координаты x(t), y(t),z(t) в базисе i,j, k. Это значит, что r(t) = x(t)+ у (t)J+ z(t)k, причем x(t), y(t), z(t) — координаты точки М в момент времени t. Простейшими линиями в пространстве Ез назовем любую прямую, отрезок и луч. Фигура Если в пространстве Ез задана прямоугольная система координат Oijk, то элементарная линия Уравнения называются параметрическими уравнениями данной линии. Линией (или кривой) называется фигура, которую можно покрыть конечным или счетным множеством элементарных линий. Пусть элементарная линия у0 определена параметрическими уравнениями x = x(t), y = y(t) z = z(t). Линия Будем называть простейшей поверхностью в пространствеE3 любую из следующих фигур: плоскость, замкнутую полуплоскость, квадрат. Элементарной поверхностью называется фигура, гомеоморфная какой-либо из простейших поверхностей. Зададим в пространстве прямоугольную систему координат Oijk и рассмотрим тот гомеоморфизм f:G->Fo, который переводит область G в элементарную поверхность F0. Если точка (u, v) Пусть F0 — элементарная поверхность, заданная параметрическими уравнениями. Поверхность F0 называется гладкой класса Ck (k — натуральное число), если правые части уравнений являются функциями, имеющими в области G непрерывные частные производные до порядка k включительно. Дифференциал векторной функции r(u, v) в произвольной точке имеет вид dr = rudu + rvdv. Отсюда следует, что (dr)2 = ф11 (du)2 + ф12dudv + ф21 dvdu + ф22 (dv)2 где ф11 = ru2, ф12 = ф21 = rurv, ф22 = rv2. Правая часть формулы является квадратичной формой. Квадратичная форма ф11 (du)2 + 2ф12dudv + ф22 (dv)2 называется первой квадратичной формой поверхности Fo или ее линейным элементом. Свойства. 1.Квадратичная форма положительно определенная, так как если du и dv не обращаются в нуль одновременно 2.Касательное векторное подпространство Тм к поверхности F0 в ее точке М является двумерным евклидовым векторным пространством. Приложения: 1. Длина дуги. Рассмотрим на поверхности Fо гладкую линию
Так как
Отсюда следует, что (ds)2 = ф11 (du)2 + 2ф12dudv + ф22 (dv)2 Таким образом, значение первой квадратичной формы поверхности представляет собой квадрат дифференциала длины дуги гладкой линии, лежащей на поверхности, при бесконечно малом смещении точки вдоль этой линии. Получаем формулу для вычисления длины дуги линии ф с концами в точках M1(t1) и М2(t2), где t1 < t2.
Таким образом, значение первой квадратичной формы поверхности представляет собой квадрат дифференциала длины дуги гладкой линии, лежащей на поверхности, при бесконечно малом смещении точки вдоль этой линии. 2. Угол между линиями. Пусть ф, ф1 — две гладкие линии на поверхности Fo, проходящие через точку М. Углом между линиями ф, ф1 называется угол между касательными к этим линиям в их общей точке М. Обозначим через d и b символы дифференцирования вдоль линий ф, ф1. Значит, dr и bг — векторы касательных к линиям ф, ф1 в точке М. Угол ф между линиями 7, 7 можно вычислить как угол между векторами dr и бг: 3. Площадь куска поверхности
К внутренней геометрии гладкой поверхности относят такие свойства этой поверхности и фигур на ней, которые определяются только первой квадратичной формой. Можно сказать, что задачи о вычислении длины дуги на поверхности, угла между линиями, площади поверхности) относятся к внутренней геометрии поверхности. Полная кривизна поверхности. Вектор нормали: Вторая квадратичная форма поверхности:
Уравнение главных кривизн:
Теорема Гаусса. Полная кривизна поверхности выражается только через коэффициенты первой квадратичной формы и их производные.
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1418; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.95.37 (0.009 с.) |

 Два многоугольника назыв равносоставленными, если один из них можно разрезать на такие части, из которых, если их сложить другим образом, можно получить второй многоугольник.
Два многоугольника назыв равносоставленными, если один из них можно разрезать на такие части, из которых, если их сложить другим образом, можно получить второй многоугольник.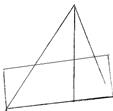 Теорема: Всякий треугольник равносоставлен с параллелограммом (одна сторона параллелограмма равна стороне треугольника и высота параллелограмма равна половине соответствующей и высоты треугольника)
Теорема: Всякий треугольник равносоставлен с параллелограммом (одна сторона параллелограмма равна стороне треугольника и высота параллелограмма равна половине соответствующей и высоты треугольника)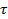 некоторое семейство множеств
некоторое семейство множеств 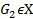 тогда будем говорить, что
тогда будем говорить, что 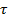 Î
Î 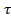
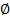 и само множество ХÎ
и само множество ХÎ  называется открытым множеством. Любое условие называется аксиомой топологического пространства. На одном том же пространстве можно вводить различные топологические пространства.
называется открытым множеством. Любое условие называется аксиомой топологического пространства. На одном том же пространстве можно вводить различные топологические пространства.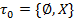 – антидискретная, тривиальная, минимальной топологии;
– антидискретная, тривиальная, минимальной топологии; = {всевозможные подмножества множества Х, Х}
= {всевозможные подмножества множества Х, Х}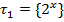 называется дискретной или максимальной. Каждая точка пространства Х считается открытым множеством.
называется дискретной или максимальной. Каждая точка пространства Х считается открытым множеством. ) — топологическое пространство, k-мерной координатной системой в этом пространстве называется гомеоморфизм ф некоторого открытого множества U
) — топологическое пространство, k-мерной координатной системой в этом пространстве называется гомеоморфизм ф некоторого открытого множества U 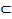 X на открытое множество числового пространстваRn. При этом пару (U, ф) называют k-мерной картой, а множество U — координатной окрестностью этой карты.
X на открытое множество числового пространстваRn. При этом пару (U, ф) называют k-мерной картой, а множество U — координатной окрестностью этой карты.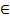 U, то ф(х) = (х1,..., xk)
U, то ф(х) = (х1,..., xk) 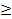 0. Следовательно, R+ — это замкнутое полупространство в Rk. Пространство (X, У) называется k-мерным многообразием с краем, если оно отделимо, имеет счетную базу и его точки можно разбить на два непустых класса так, что каждая из точек одного класса (точки внутренние) имеет окрестность, гомеоморфную пространству R\ а каждая из точек другого класса (точки краевые) имеет окрестность, гомеоморфную R+, но не имеет окрестности, гомеоморфной Rk.
0. Следовательно, R+ — это замкнутое полупространство в Rk. Пространство (X, У) называется k-мерным многообразием с краем, если оно отделимо, имеет счетную базу и его точки можно разбить на два непустых класса так, что каждая из точек одного класса (точки внутренние) имеет окрестность, гомеоморфную пространству R\ а каждая из точек другого класса (точки краевые) имеет окрестность, гомеоморфную R+, но не имеет окрестности, гомеоморфной Rk. j) либо пусто, либо является вершиной этих клеток, либо стороной каждой из них.
j) либо пусто, либо является вершиной этих клеток, либо стороной каждой из них.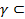 F называется стороной разложения K, если она является стороной хотя бы одной клетки из К. Введем обозначения:
F называется стороной разложения K, если она является стороной хотя бы одной клетки из К. Введем обозначения: 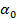 — число вершин,
— число вершин, 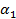 — число сторон,
— число сторон, 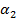 — число клеток разложения K.
— число клеток разложения K.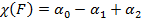 называется эйлеровой характеристикой многообразия F.
называется эйлеровой характеристикой многообразия F.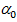 - число вершин,
- число вершин,  - число ребер,
- число ребер,  – число граней простого многогранника, то имеет место равенство:
– число граней простого многогранника, то имеет место равенство:
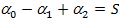
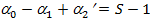
 – всего ребер
– всего ребер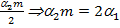
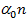 - всего ребер;
- всего ребер;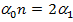
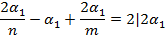
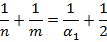
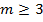

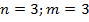 - тетраэдр
- тетраэдр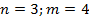 - куб
- куб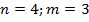 - октаэдр
- октаэдр - икосаэдр
- икосаэдр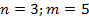 - додекаэдр
- додекаэдр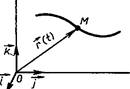 Пусть точка М движется в евклидовом пространстве Е3. Зададим в пространстве прямоугольную систему координат Oijk. Положение частицы в момент времени t (из некоторого временного промежутка J можно определить радиус-вектором r(t) точки М относительно точки О. Когда t меняется в промежутке J, мы получаем
Пусть точка М движется в евклидовом пространстве Е3. Зададим в пространстве прямоугольную систему координат Oijk. Положение частицы в момент времени t (из некоторого временного промежутка J можно определить радиус-вектором r(t) точки М относительно точки О. Когда t меняется в промежутке J, мы получаем определяется системой уравнений х = x(t), у = y(t), z = z(t), где t изменяется в некотором промежутке J, а правые части в формулах— непрерывные в промежутке J функции.
определяется системой уравнений х = x(t), у = y(t), z = z(t), где t изменяется в некотором промежутке J, а правые части в формулах— непрерывные в промежутке J функции.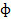 : u = u(t) v = v(t), где параметр t изменяется в некотором промежутке J. Линия
: u = u(t) v = v(t), где параметр t изменяется в некотором промежутке J. Линия 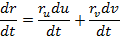
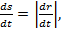 где s — длина дуги линии
где s — длина дуги линии 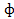 , то из этой формулы находим:
, то из этой формулы находим: