
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение прямых, лучей, отрезков, плоскостей.Содержание книги
Поиск на нашем сайте
Из анализа аксиоматики Вейля видно, что она в основном явл-ся векторной. A, B – точки, Опр. Множ-во точек M таких, что (AM) ={M: Если Пусть даны 3 точки: M1( Опр. Буд.гов., что M2 лежит между M1 и M3, если M1 Имея понятие «между» мож.напис.понятие отрезка Опр. Отрезком буд.наз-ть мн-во точек, сост.из M1,M3 и точек, лежащих между M1 и M3; M1 и M3 – концы отрезка Опр. Отрезком AB явл-ся мн-во точек, значение параметра Опр. Лучом [AB) буд.наз-ть мн-во точек, знач-е параметра Свойства прямой: 1. 2. Прямая определ-ся однозначно любыми 2-мя ее разл.точками Пусть даны 3 разл.точки,не леж.на одной прямой. Опр. мн-во точек M таких, что (A,B,C)={M:
если u,v =0 => M совпад.с A; если u=1,v =0 => M совпад. с B; если u =0,v =1 => M совпад.с C. u,v – параметры, фиксир.точку М.; А-нач.точка; М-текущая точка св-ва плоскости: 1. А,В,С принадл.пл-ти 2. На пл-ти сущ-т бесчисл.мн-во точек, среди них хотя бы одна тройка точек не лежит на одной прямой 3. Пл-ть вполне опред-ся любыми 3-мя ее неколлин-ми точками опр. Если в ур-ии пл-ти u опр. Пересечение полуплоскостей (АС, В) и (АВ,С) буд. наз-ть углом ВАС
Многоугольники. Площадь многоугольника. Теорема существования и единственности. Равновеликость и равносоставленность. Понятие простого многоугольника Основная фигура – многоугольник. 0:Многоугольник будем называть простым, если все его вершины различные, ни одна вершина не явл внутренней точкой стороны и никакие две стороны не пересекаются во внутренней точке Будем говорить что многоугольник Р разбит на 2 многоугольника– Р1 и Р2 и он является суммой Р=Р1 + Р2 Определение площади многоугольника. 0: Пусть каждому многоугольнику Р поставлено в соответствие положительное число S(H)>0 так что при этом выполняются следующие аксиомы: 1) Равным многоугольникам соответствуют равные числа P=Q ⇒S(P)=S(Q) 2) Если многоугольник разбит на 2 многоугольника Р1 и Р2 то многоугольнику Р ставится в соответствие число, равное сумме чисел поставленных в соответствие многоугольникам Р=Р1 + Р2 ⇒S(P)=S(Р1) + S(Р2) 3) Квадрату, сторона которого равна единице длины ставится в соответствие число равное 1 Тогда число S(P) будем называть площадью многоугольника, а квадрат 3) будем называть единицей площади Теорема существования и единственности площади простого многоугольника.
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 606; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.88.141 (0.007 с.) |

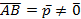
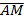 коллинеарен
коллинеарен  , т.е.
, т.е. 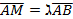 будем называть прямой (
будем называть прямой (
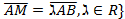 , где
, где  , A – нач.точка,
, A – нач.точка, 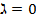 => M совпадает с A; Если
=> M совпадает с A; Если 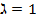 => M=B.
=> M=B. M2(
M2(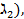 M3(
M3(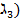
 M2
M2  M3 три различные точки и
M3 три различные точки и  .
. которых принадл.[0,1].
которых принадл.[0,1].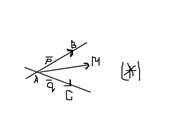 На прямой
На прямой  бесчисл.мн-во точек
бесчисл.мн-во точек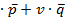 буд.наз. плоскостью (u,v
буд.наз. плоскостью (u,v 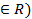
 = u
= u 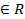 }
} , v-произв.зн-е, то получ. полуплоскость с границей АС. (АС, В)
, v-произв.зн-е, то получ. полуплоскость с границей АС. (АС, В)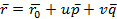 - векторно-парам.ур-е пл-ти.
- векторно-парам.ур-е пл-ти.


